Abstract
本文提出一种低秩张量限制的多视图子空间聚类方法（LR-MSC）。这个方法是属于多视图子空间类别。该方法是将从不同视图中学习到的子空间表示矩阵看成一个张量，张量可以捕获多视图数据之间的高阶相关性。再对这个张量施加低秩约束，这个约束可以优雅的建模不同视图之间的交叉信息，从而有效的减少子空间表示的冗余，提高聚类的精确度。通过增广的拉格朗日交替方向乘子法(AL-ADM) 有效的解决优化问题，在各种实验数据集上证明了该方法的有效性。
2. Relate work
ps:以往重复的就不再提及s
3.The Proposed Approach
3.1张量知识拓展
在此处扩展一下关于张量的知识点，对于一些基础概念我就不一一赘述，我只简单的提及一下，张量可以把它想象成一个盛放数据的容器，它有很多种形式，其实在最早接触数学知识的时候，我们也接触到了张量，比如我们把0维张量看作一个标量，即一个数字；把数组看做1维张量，把矩阵看做2维张量，把矩阵的叠加看做一个三维张量，只是名字换了而已。因为本篇论文的研究只用到三维张量，就不往4维或者更高维的张量拓展了。结合下面的图可能更容易理解：
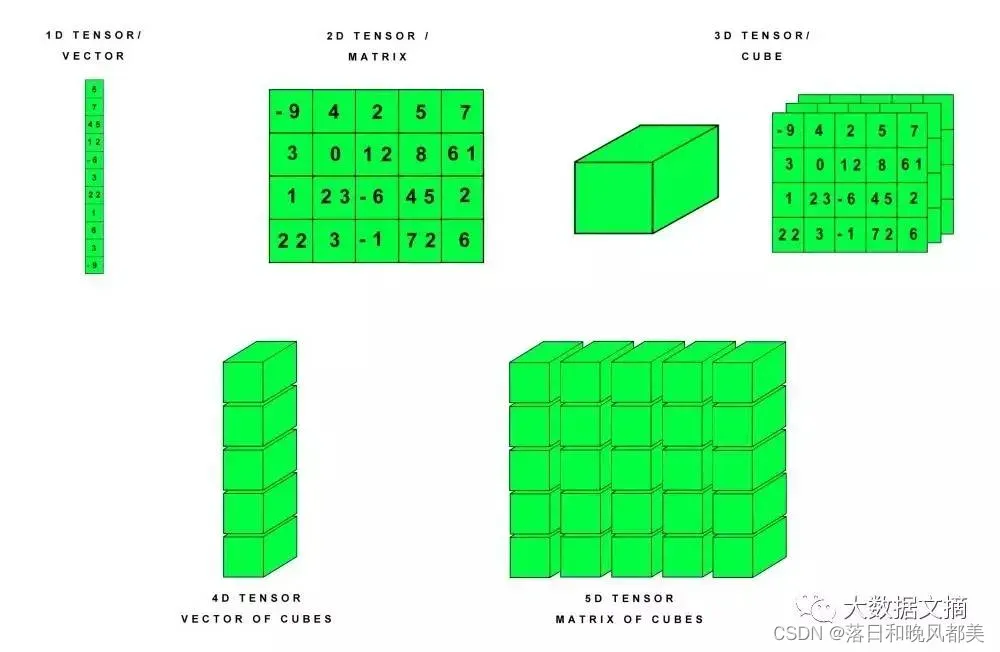当然，仅仅了解张量的概念是远远不够的，我们还需要了解张量的展开和张量核范数，具体内容会以PPT的形式呈现，如果想更深入了解，可以参考https://zhuanlan.zhihu.com/p/37900429
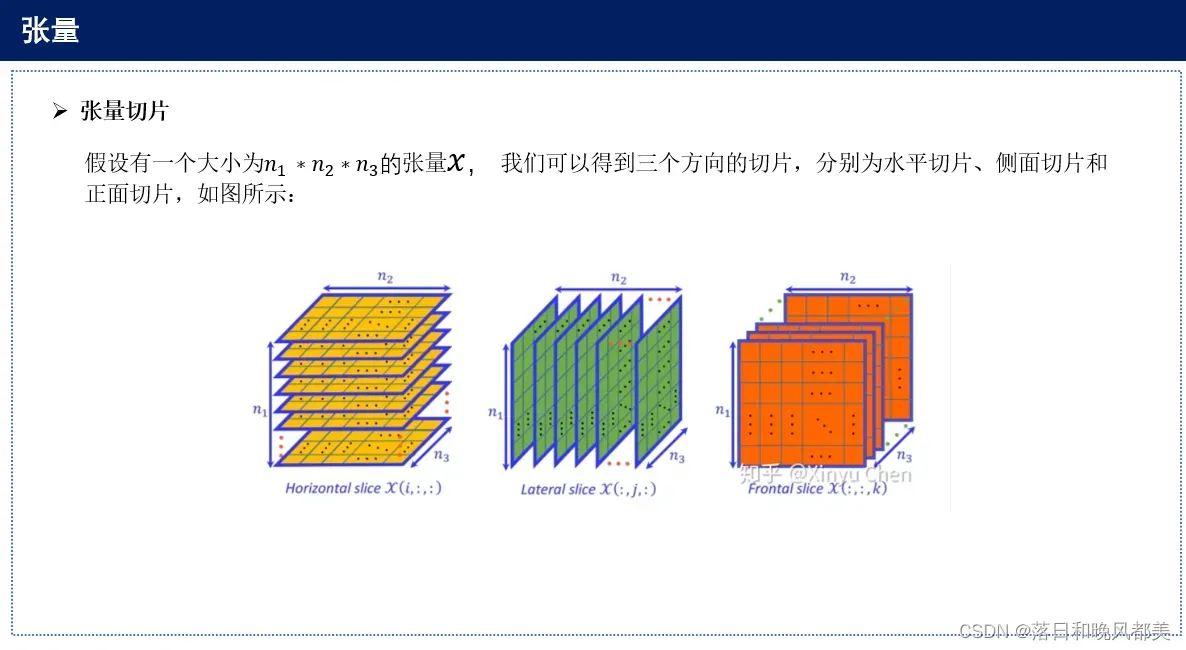
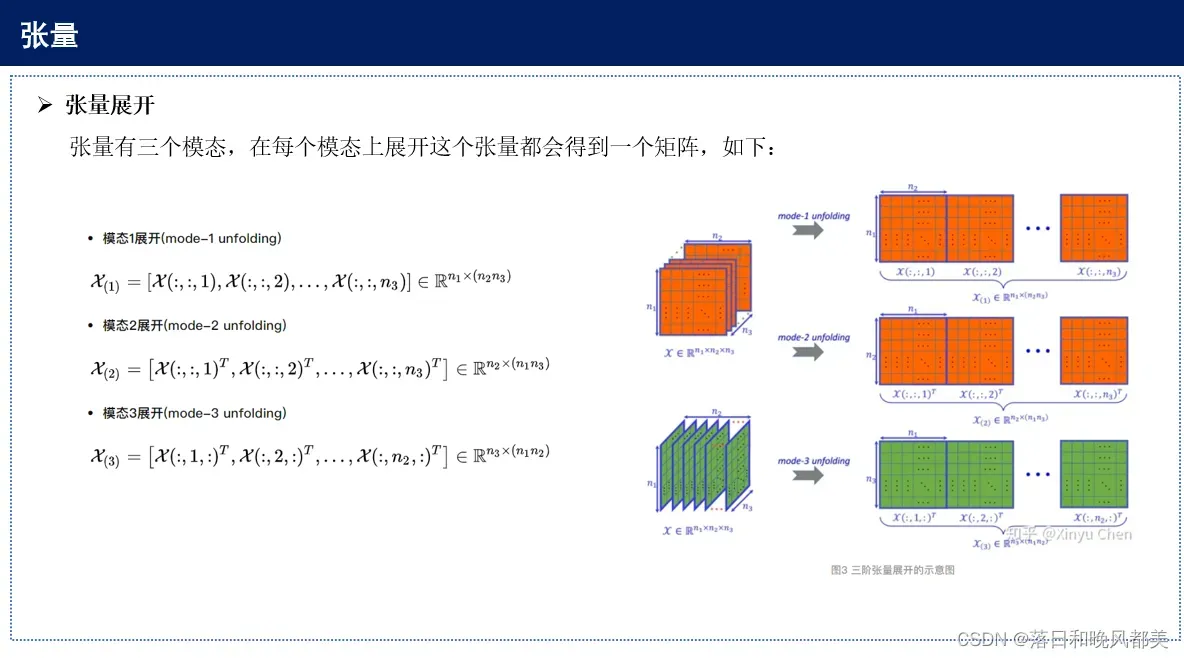
3.2 Formulation
3.3 Optimization Procedure
插播点别的话题，因为现在我觉得到一篇文章最难的地方了，就是涉及到优化部分，一般和数学公式推导沾边的，真的很让人头疼，对于我读过的论文的优化部分，之前总是一知半解，只看到论文上给的子问题优化的公式，然后说引用了哪篇文献的解决办法来解决这个问题，然后就直接给出最优解的公式。在我们论文对应的代码部分，对于使用增广的拉格朗日交替方向乘子法进行优化，里面每个子问题的优化，只需要将最优解公式转化成代码就行了，也没有具体求解的步骤。虽然我知道这是优化哪一个子问题，但是我具体如何求解的还是很模糊。以至于当我看某一篇论文的时候，是有了idea，有了想法，那下一步我基本上是将目标函数写出来，然后写出其对应的增广的拉格朗日函数，下一步就是分成子问题进行优化，对于我自己写出的目标函数子问题待优化的部分，我就不知道如何求解，可能会涉及到梯度上升法，或者关于范数优化问题，我也不能确定自己求解出来的公式对不对。所以，如果有缘人看到这篇文章，有相应的解决办法，或者说有什么工具，可以不用手动求解更好，可以私信我，让我们分享知识，传播智慧。
当然，我知道，因为涉及了很多凸优化的知识，可能学习一些关于凸优化的理论，这个工程量也是很繁琐的，短时间很难看到效果（只是个人拙见，不喜勿喷）。
我也打算在接下来的时间段，深入了解关于优化部分的求解，然后出一期对于多视图方向目标函数优化问题详细讲解的文章，因为我发现现在发在网上的关于这个方向的论文笔记，都没有涉及到这个问题，这个问题困扰我很久，我希望自己能解决，从而也帮助那些深受优化折磨的同伴们。好啦，巴拉巴拉太多了，现在开始正题。
文章出处登录后可见！
