蚁群算法

Ant Colony Optimization
文章链接https://gitee.com/fakerlove/machine-learning/tree/master/13-intelligent-optimization-algorithms
观看视频链接：https://www.bilibili.com/video/BV1vp4y1p78R

1. 简介

1.1 简介

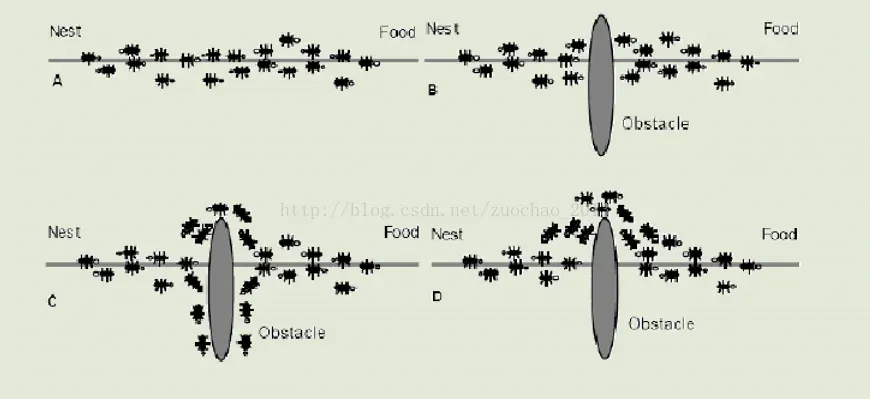
蚁群算法(ACO)是一种模拟蚂蚁觅食行为的模拟优化算法，它是由意大利学者Dorigo M等人于1991年首先提出，并首先使用在解决TSP（旅行商问题）上。

自然界中有一个神奇的现象，即蚂蚁在没有提示的情况下总是能够找到从巢穴到食物的最短路径，这是为什么呢？原因就是蚂蚁在寻找食物时，能在其走过的路径上释放一种特殊的分泌物——信息素，随着时间的推移该物质会逐渐挥发，后来的蚂蚁会根据信息素的强度来选择要走的路径。由于越短的路径单位时间内蚂蚁走过的次数越多，所以留下的信息素越多，这就导致后来的蚂蚁选择该路径的概率越大，从而形成一种正反馈机制，最终找到最优路径。正式由于对蚂蚁寻找食物的发现与模拟，意大利学者M.Dorigo，V.Maniezzo和A.Colorni等人于20世纪90年代初期，通过模拟自然界中蚂蚁集体寻径行为而提出的一种基于种群的启发式随机搜索算法——蚁群算法。

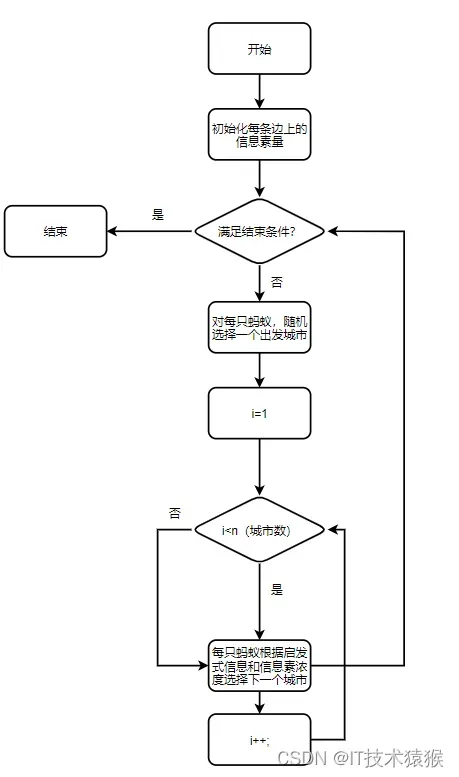
1.2 蚁群流程图

蚁群算法的基本原理:

1、蚂蚁在路径上释放信息素。

2、碰到还没走过的路口，就随机挑选一条路走。同时，释放与路径长度有关的信息素。

3、信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高路径。

4、最优路径上的信息素浓度越来越大。

5、最终蚁群找到最优寻食路径。

1.3 分类(可以不看)

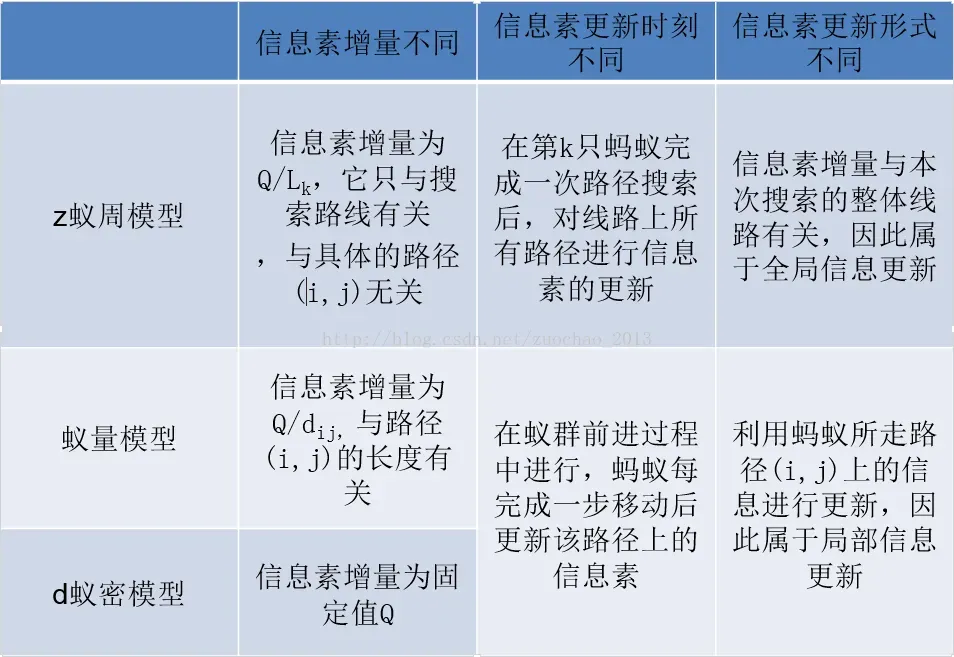
蚁周模型（Ant-Cycle模型）

蚁量模型（Ant-Quantity模型）

蚁密模型（Ant-Density模型）

区别：

1.蚁周模型利用的是全局信息，即蚂蚁完成一个循环后更新所有路径上的信息素；

2.蚁量和蚁密模型利用的是局部信息，即蚂蚁完成一步后更新路径上的信息素。

2. 算法

2.1 参数讲解

m-蚂蚁数量

k-蚂蚁编号

t-时刻

n-表示城市数量

–表示城市之间的距离

–启发式因子(能见度)，反映蚂蚁由城市转移到城市的启发程度

–边上的信息素

–本次迭代边上信息素增量

–第k只蚂蚁在本次迭代中留在边上的信息素量

–信息素挥发（或挥发）系数

–持久性（或残留）系数

–时刻t蚂蚁由城市转移到城市的概率（转移概率）

–蚂蚁k的禁忌表

定义	参数影响分析	取值范围
m	蚂蚁数量	m数目越多，得到的最优解就越精确，但是会产生不少重复解，随着算法接近最优值的收敛，信息正反馈作用降低，大量的重复工作，消耗了资源，增加了时间复杂度
	信息挥发因子	过小时，在各路径上残留的信息素过多，导致无效的路径继续被搜索，影响到算法的收敛速率;过大，无效的路径虽然可以被排除搜索，但是不能保证有效的路径也会被放弃搜索，影响到最优值的搜索	[0.1,0.99]

2.2 计算公式

1) 转移概率公式

—信息素的相对重要重要程度

—启发式因子的相对重要程度

–蚂蚁k下一步允许选择的城市集合

定义	参数影响分析	取值范围
	信息启发式因子	值越大，蚂蚁选择之前走过的路径可能性就越大，搜索路径的随机性减弱，越小，蚁群搜索范围就会减少，容易陷入局部最优	[0,5]
	期望启发式因子	β值越大，蚁群就越容易选择局部较短路径，这时算法的收敛速度是加快了，但是随机性却不高，容易得到局部的相对最优	[0,5]

2) 启发式因子计算公式

3) 信息素计算公式

当所有蚂蚁完成一次周游后，各路径上的信息素为

第一部分挥发后信息素，第二部分，t时刻的该路径信息素的增量

,如果蚂蚁k在本次周游中经过边

定义	取值范围
	正常数,路径信息素常量	[10,1000]
	蚂蚁k在本次周游中所走路径的长度

开始时，令

2.2 算法流程图

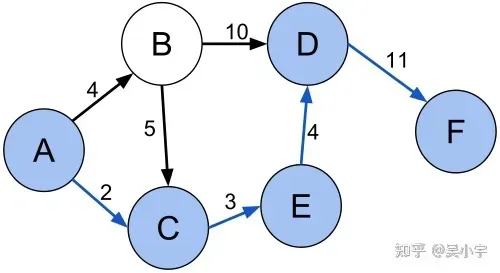
2.3 解决TSP问题

在tsp中可以模拟蚂蚁在两两城市之间所留下信息素，来搜索最短路径

简单计算下蚂蚁是如何寻找最短路径的：

假设蚂蚁从A点出发，目的是F点，上诉图片中共有三条路径：

A——>B——>D——>F
A——>C——>E——>D——>F
A——>B——>C——>E——>D——>F

注意点，
第一点，蚂蚁是不会走重复的路。所以做了蚂蚁一定会从A-F的假设
第二点，此题，我们是假设3只蚂蚁把上面的3个路线都走了。实际情况肯定不是这样子的

上诉三条路径长度分别为
- L1 =4+10+11=25,
- L2 = 2+3+4+11=20,
- L3=4+5+3+4+11=27
蚂蚁访问数量分别为n1=n2=n3=1
初始化个点之间的信息素是相同的，每个点被访问的概率也是相同的(例如A点到B或者到C的概率都是0.5)

那么，三条路径，三只蚂蚁访问后，每个节点留下的信息素如下：

A-C有一只蚂蚁访问，留下信息素为:
A-B有两只蚂蚁访问，留下信息素为 :
B-C 1只蚂蚁访问，留下信息素为：
B-D 1只蚂蚁访问，留下信息素为
C-E 两只蚂蚁访问，留下信息素为：
E-D两只蚂蚁访问，留下信息素为:
D-F三只蚂蚁访问，留下信息素为：

根据信息素，从A到B 、C点的选择概率为

我们发现一个问题，最优路径是A-C-E-D-F，而A点出发，B点被选择的概率远大于C点被选择的概率，因此计算信息素时就要加入两个城市之间的距离信息和一些因子。

信息启发因子，值越大，则蚂蚁选择之前走过的路径可能性就越大，值越小，则蚁群搜索范围就会减少，容易陷入局部最优。

值越大，蚁群越就容易选择局部较短路径，这时算法收敛速度会加快，但是随机性不高，容易得到局部的相对最优。

2.4 优缺点

与其他优化算法相比，蚁群算法具有以下几个特点：

(1)采用正反馈机制，使得搜索过程不断收敛，最终逼近最优解。

(2)每个个体可以通过释放信息素来改变周围的环境，且每个个体能够感知周围环境的实时变化，个体间通过环境进行间接地通讯。

(3)搜索过程采用分布式计算方式，多个个体同时进行并行计算，大大提高了算法的计算能力和运行效率。

(4)启发式的概率搜索方式不容易陷入局部最优，易于寻找到全局最优解。

3. 代码

3.1 matlab

没有验证过，网上copy的代码

clear;
close all;
clc;
C = [1304 2312;         % 城市坐标
    3639 1315;
    4177 2244;
    3712 1399;
    3488 1535;
    3326 1556;
    3238 1229;
    4196 1044;
    4312 790;
    4386 570;
    3007 1970;
    2562 1756;
    2788 1491;
    2381 1676;
    1332 695;
    3715 1678;
    3918 2179;
    4061 2370;
    3780 2212;
    3676 2578;
    4029 2838;
    4263 2931;
    3429 1980;
    3507 2376;
    3394 2643;
    3439 3201;
    2935 3240;
    3140 3550;
    2545 2357;
    2778 2826;
    2370 2975];
% figure(1);
% scatter(C(:,1),C(:,2),'k','d');
% title('城市分布图');
 
[M,N] = size(C);
% M为问题的规模  M个城市
distance = zeros(M,M);     % 用来记录任意两个城市之间的距离
% 求任意两个城市之间的距离
for m=1:M
    for n=1:M
        distance(m,n) = sqrt(sum((C(m,:)-C(n,:)).^2));
    end
end
m = 50;   % 蚂蚁的个数   一般取10-50    
alpha = 1;   %  信息素的重要程度    一般取【1,4】
beta = 5;    %  启发式英子的重要程度   一般取【3,5】
rho = 0.25;    % 信息素蒸发系数
G = 150;
Q = 100; % 信息素增加系数
Eta = 1./distance;  % 启发式因子
Tau = ones(M,M);  % 信息素矩阵  存储着每两个城市之间的信息素的数值
Tabu = zeros(m,M);  % 禁忌表，记录每只蚂蚁走过的路程
gen = 1;  
R_best = zeros(G,M);  % 各代的最佳路线
L_best = inf.*ones(G,1);   % 每一代的最佳路径的长度     初始假设为无穷大
%   开始迭代计算
while gen<G
    %  将m只蚂蚁放到n个城市上
    random_pos = [];
    for i=1:(ceil(m/M))  % m只蚂蚁随即放到M座城市 
        random_pos = [random_pos,randperm(M)];   %  random_pos=[1~31 + 1~31]   将每只蚂蚁放到随机的城市  在random_pos 中随机选择m个数，代表蚂蚁的初始城市
    end
    Tabu(:,1) = (random_pos(1,1:m))';   % 第一次迭代每只蚂蚁的禁忌表
    
    for i=2:M      %  从第二个城市开始
        for j=1:m   %  每只蚂蚁
            visited = Tabu(j,1:(i-1));   %  在访问第i个城市的时候，第j个蚂蚁访问过的城市
            % visited=visited(1,:);
            unvisited = zeros(1,(M+1-i));  %  待访问的城市
            visit_P = unvisited;   %  蚂蚁j访问剩下的城市的概率
            count = 1;
            for k=1:M   % 这个循环是找出未访问的城市  
                if isempty(find(visited==k))   %还没有访问过的城市  如果成立。则证明第k个城市没有访问过
                    unvisited(count) = k;
                    count = count+1;
                end
            end
            %  计算待选择城市的概率
            for k=1:length(unvisited)    % Tau(visited(end),unvisited(k))访问过的城市的最后一个与所有未访问的城市之间的信息素
                visit_P(k) = ((Tau(visited(end),unvisited(k)))^alpha)*(Eta(visited(end),unvisited(k))^beta);
            end
            visit_P = visit_P/sum(visit_P);   %  访问每条路径的概率的大小
            %   按照概率选择下一个要访问的城市
            %   这里运用轮盘赌选择方法      这里也可以选择选择概率最大的路径去走， 这里采用轮盘赌选择法。
            Pcum = cumsum(visit_P);
            selected = find(Pcum>=rand);
            to_visited = unvisited(selected(1));
            Tabu(j,i) = to_visited;  % 添加到禁忌表
        end
    end
    if gen>=2
        Tabu(1,:) = R_best(gen-1,:);
    end
    %  记录m只蚂蚁迭代的最佳路线
    L = zeros(1,m);
    for i=1:m
        R = Tabu(i,:);
        L(i) = distance(R(M),R(1));   % 因为要走一周回到原来的地点    
        for j=1:(M-1)
            L(i) = L(i)+distance(R(j),R(j+1));
        end
    end
    L_best(gen) = min(L);    %  记录每一代中路径的最短值
    pos = find(L==L_best(gen));
    R_best(gen,:) = Tabu(pos(1),:);   % 最优的路径
    
    %  更新信息素的值
    Delta_Tau = zeros(M,M);
    for i=1:m   %  m只蚂蚁
        for j=1:(M-1)   %  M座城市
            Delta_Tau(Tabu(i,j),Tabu(i,j+1)) = Delta_Tau(Tabu(i,j),Tabu(i,j+1)) + Q/L(i);    %  m只蚂蚁的信息素累加 这里采用的是论文中ant-cycle模型
        end
        Delta_Tau(Tabu(i,M),Tabu(i,1)) = Delta_Tau(Tabu(i,M),Tabu(i,1)) + Q/L(i);
    end
    Tau = (1-rho).*Tau+Delta_Tau;   % 更新路径上的信息素含量
    %  禁忌表清零
    Tabu = zeros(m,M);
    
    for i=1:(M-1)
        plot([C(R_best(gen,i),1),C(R_best(gen,i+1),1)],[C(R_best(gen,i),2),C(R_best(gen,i+1),2)],'bo-');
        hold on;
    end
    plot([C(R_best(gen,n),1),C(R_best(gen,1),1)],[C(R_best(gen,n),2),C(R_best(gen,1),2)],'ro-');
    title(['最短路径：',num2str(L_best(gen))]);
    hold off;
    pause(0.05);
    gen = gen+1;
end
figure(2);
plot(L_best);
title('路径长度变化曲线');
xlabel('迭代次数');
ylabel('路径长度数值');

3.2 python

import numpy as np
import matplotlib.pyplot as plt
import pylab

coordinates = np.array([[565.0, 575.0], [25.0, 185.0], [345.0, 750.0], [945.0, 685.0], [845.0, 655.0],
                        [880.0, 660.0], [25.0, 230.0], [525.0, 1000.0], [580.0, 1175.0], [650.0, 1130.0],
                        [1605.0, 620.0], [1220.0, 580.0], [1465.0, 200.0], [1530.0, 5.0], [845.0, 680.0],
                        [725.0, 370.0], [145.0, 665.0], [415.0, 635.0], [510.0, 875.0], [560.0, 365.0],
                        [300.0, 465.0], [520.0, 585.0], [480.0, 415.0], [835.0, 625.0], [975.0, 580.0],
                        [1215.0, 245.0], [1320.0, 315.0], [1250.0, 400.0], [660.0, 180.0], [410.0, 250.0],
                        [420.0, 555.0], [575.0, 665.0], [1150.0, 1160.0], [700.0, 580.0], [685.0, 595.0],
                        [685.0, 610.0], [770.0, 610.0], [795.0, 645.0], [720.0, 635.0], [760.0, 650.0],
                        [475.0, 960.0], [95.0, 260.0], [875.0, 920.0], [700.0, 500.0], [555.0, 815.0],
                        [830.0, 485.0], [1170.0, 65.0], [830.0, 610.0], [605.0, 625.0], [595.0, 360.0],
                        [1340.0, 725.0], [1740.0, 245.0]])  # 城市坐标


def getdistmat(coordinates):
    num = coordinates.shape[0]
    distmat = np.zeros((52, 52))  # 打印一个52行52列的二维数组
    for i in range(num):
        for j in range(i, num):
            distmat[i][j] = distmat[j][i] = np.linalg.norm(coordinates[i] - coordinates[j])
    return distmat  # distmat[i][j] = distmat[j][i]表示城市i和j距离


distmat = getdistmat(coordinates)  # 二维数组，表示城市之间的距离
numant = 40  # 蚂蚁个数
numcity = coordinates.shape[0]  # 城市个数   shape[0]输出二维数组【numpy】的行数。
alpha = 1  # 信息素重要程度因子
beta = 5  # 启发函数重要程度因子
rho = 0.1  # 信息素的挥发速度
Q = 1  # 信息素强度
iter = 0
itermax = 250
etatable = 1.0 / (distmat + np.diag([1e10] * numcity))  # 启发函数矩阵，表示蚂蚁从城市i转移到矩阵j的期望程度
pheromonetable = np.ones((numcity, numcity))  # 信息素矩阵        52行52列的二维数组。元素都是1
pathtable = np.zeros((numant, numcity)).astype(int)  # 路径记录表    40行52列的二维数组，目前都为0
# distmat = getdistmat(coordinates)  # 城市的距离矩阵
lengthaver = np.zeros(itermax)  # 各代(各个循环)路径的平均长度          # 一维数组，itermax个0
lengthbest = np.zeros(itermax)  # 各代及其之前遇到的最佳路径长度    # 一维数组，itermax个0
pathbest = np.zeros((itermax, numcity))  # 各代及其之前遇到的最佳路径长度         # itermax(250)行numcity(52)列的二维矩阵

while iter < itermax:  # 循环0-250次
    # 1、随机产生各个蚂蚁的起点城市
    if numant <= numcity:  # 1.1、城市数比蚂蚁数多
        #  permutation()：随机排列序列，生成一个0-52的一维数组,[:numant]去除前numant个分配给pathtable中的第0列
        pathtable[:, 0] = np.random.permutation(range(0, numcity))[:numant]
    else:  # 1.2、蚂蚁数比城市数多，需要补足
        pathtable[:numcity, 0] = np.random.permutation(range(0, numcity))[:]  # 先将城市全部取出，剩下的蚂蚁随机分配
        # 剩下numant - numcity个蚂蚁，将分配给他们的城市数分配在他们的第0列
        pathtable[numcity:, 0] = np.random.permutation(range(0, numcity))[:numant - numcity]
    length = np.zeros(numant)  # 计算各个蚂蚁的路径距离，还未走,都是0.
    # 2、各个蚂蚁进行路径选择
    for i in range(numant):
        visiting = pathtable[i, 0]  # 当前所在的城市，将[i,0]位置的值赋值给visiting
        unvisited = set(range(numcity))  # 未访问的城市,以集合的形式存储{}
        unvisited.remove(visiting)  # 删除元素；利用集合的remove方法删除存储的数据内容
        # 3、循环numcity-1次，访问剩余的numcity-1个城市，循环为一只蚂蚁访问所有城市的过程
        for j in range(1, numcity):
            # 每次用轮盘法选择下一个要访问的城市
            listunvisited = list(unvisited)      # 列表,即为一维数组。
            probtrans = np.zeros(len(listunvisited))   # 创建一个【未被访问城市个数】一维数组,s元素全为0
            for k in range(len(listunvisited)):
                probtrans[k] = np.power(pheromonetable[visiting][listunvisited[k]], alpha) \
                               * np.power(etatable[visiting][listunvisited[k]], beta)
            cumsumprobtrans = (probtrans / sum(probtrans)).cumsum()    # cumsum()将probtrans数组中的值进行累加求和
            cumsumprobtrans -= np.random.rand()
            k = listunvisited[(np.where(cumsumprobtrans > 0)[0])[0]]  # python3中原代码运行bug，类型问题；鉴于此特找到其他方法
            # 通过where（）方法寻找矩阵大于0的元素的索引并返回ndarray类型，然后接着载使用[0]提取其中的元素，用作listunvisited列表中
            # 元素的提取（也就是下一轮选的城市）
            pathtable[i, j] = k  # 添加到路径表中（也就是蚂蚁走过的路径)，第i号蚂蚁第j步走的城市。
            unvisited.remove(k)  # 然后在为访问城市set中remove（）删除掉该城市
            length[i] += distmat[visiting][k]    # 当前所在城市visiting到城市k的距离，length[]用于存储各个蚂蚁走的路径长度，一维数组。
            visiting = k
        length[i] += distmat[visiting][pathtable[i, 0]]  # 蚂蚁的路径距离包括最后一个城市和第一个城市的距离  TSP问题，访问所有城市后又回到了原点
        # 包含所有蚂蚁的一个迭代结束后，统计本次迭代的若干统计参数
    # 4、从当前循环中找出最小路径和最小路径长度并保存
    lengthaver[iter] = length.mean()   # 各代(各个循环)路径的平均长度
    if iter == 0:
        lengthbest[iter] = length.min()                      # length[]记录的是当前循环，每个蚂蚁走出的路径长度
        pathbest[iter] = pathtable[length.argmin()].copy()   # length.argmin()显示length[]中最小值的下标
    else:
        if length.min() > lengthbest[iter - 1]:              # 当前循环中的最小路径不是最优值
            lengthbest[iter] = lengthbest[iter - 1]
            pathbest[iter] = pathbest[iter - 1].copy()
        else:
            lengthbest[iter] = length.min()
            pathbest[iter] = pathtable[length.argmin()].copy()
    # 5、更新信息素
    changepheromonetable = np.zeros((numcity, numcity))
    for i in range(numant):
        for j in range(numcity - 1):
            # 更新蚂蚁i从城市j到j+1路径的信息素
            changepheromonetable[pathtable[i, j]][pathtable[i, j + 1]] += Q / distmat[pathtable[i, j]][
                pathtable[i, j + 1]]  # 计算信息素增量
        # 最后一个城市到第一个城市途径的信息素增量
        changepheromonetable[pathtable[i, j + 1]][pathtable[i, 0]] += Q / distmat[pathtable[i, j + 1]][pathtable[i, 0]]
    # 带入计算信息素公式，更新完毕，本次循环结束
    pheromonetable = (1 - rho) * pheromonetable + changepheromonetable  # 计算信息素公式
    iter += 1  # 迭代次数指示器+1
    print("iter:", iter)

# 做出平均路径长度和最优路径长度
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(12, 10))
axes[0].plot(lengthaver, 'k', marker=u'')
axes[0].set_title('Average Length')
axes[0].set_xlabel(u'iteration')

axes[1].plot(lengthbest, 'k', marker=u'')
axes[1].set_title('Best Length')
axes[1].set_xlabel(u'iteration')
fig.savefig('average_best.png', dpi=500, bbox_inches='tight')
plt.show()

# 作出找到的最优路径图
bestpath = pathbest[-1]   # 每次更新后，pathbest[-1]的最后一行，就是最优路径了
plt.plot(coordinates[:, 0], coordinates[:, 1], 'r.', marker=u'$\cdot$')
plt.xlim([-100, 2000])
plt.ylim([-100, 1500])

for i in range(numcity - 1):
    m = int(bestpath[i])
    n = int(bestpath[i + 1])
    plt.plot([coordinates[m][0], coordinates[n][0]], [coordinates[m][1], coordinates[n][1]], 'k')  # k为黑色
plt.plot([coordinates[int(bestpath[0])][0], coordinates[int(n)][0]],
         [coordinates[int(bestpath[0])][1], coordinates[int(n)][1]], 'b')  # 最后一个城市与第一个城市连线。 b为蓝色
ax = plt.gca()
ax.set_title("Best Path")
ax.set_xlabel('X axis')
ax.set_ylabel('Y_axis')

plt.savefig('best path.png', dpi=500, bbox_inches='tight')
plt.show()

参考资料

蚁群算法（Ant Colony Optimization）_明之季的博客-CSDN博客_蚁群算法
蚁群算法(ant colony optimization, ACO) – 知乎 (zhihu.com)
干货|十分钟快速get蚁群算法（附代码） – 知乎 (zhihu.com)
智能优化算法之蚁群算法代码实现【python、matlab】_捌椒的博客-CSDN博客_蚁群算法代码

文章出处登录后可见！

已经登录？立即刷新

蚁群算法ACO