文献地址：论文链接，Github代码：Github链接

1 研究背景

现有基于伪标签的半监督学习方法存在的问题：

伪标签 → 存在确认偏差（Confirmation Bias）
分布外噪声数据 → 影响模型的判别能力
是否存在一种通用增益方法，可适用于各基于伪标签的半监督方法？
- MixMatch[1](NIPS, 2019)：数据Mixup → 预测锐化（Sharpen）
- FixMatch[2](NIPS, 2020)：置信度阈值，弱增强 → 生成伪标签 → 监督强增强

2 关键卖点

提出一套缓解确认偏差（Confirmation Bias）的通用架构：
- 对于可靠的分布内数据（In-distribution Data）：使用有监督对比学习。
  - 分布内数据：指无标记数据集不包含新类别，或具有平衡的数据分布的数据。
- 对于存在噪声的分布外数据（Out-of-distribution Data）：对特征进行无监督对比学习。
  - 分布外数据：指无标记数据集包含未知类别，或具有不平衡的数据分布的数据。
针对伪标签存在的噪声问题：进行权重分配。

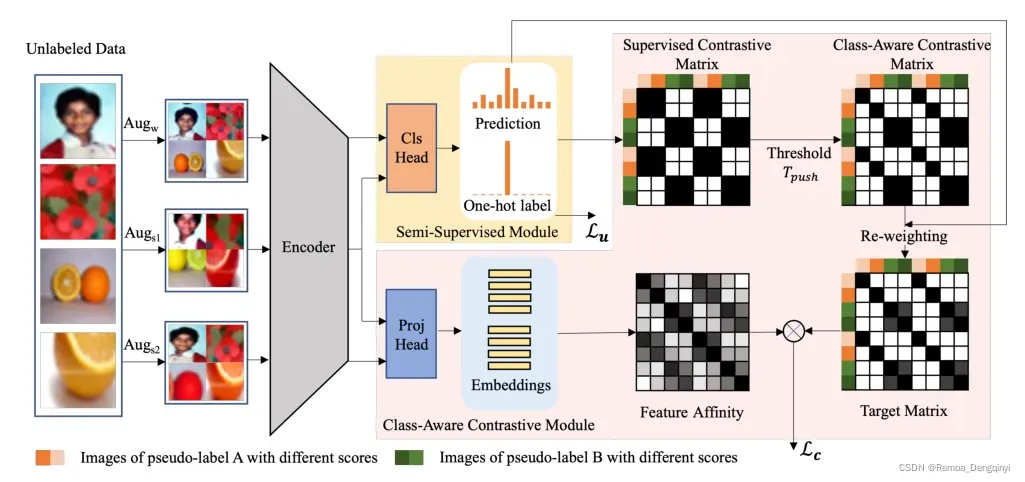
3 主要架构

整体架构目标：最小化相似性矩阵（Feature Affinity）和目标矩阵（Target Matrix）之间的有监督对比损失 $L_{con}$ ，无标签的强增强样本与弱增强样本生成的伪标签之间的交叉熵损失 $L_{u}$ ，以及有标签样本的交叉熵损失 $L_{x}$ 。即 $\mathcal{L}=\mathcal{L}_{x}+\lambda_{u} \mathcal{L}_{u}+\lambda_{c} \mathcal{L}_{c}$ 。
对于有标签样本：采用图像的弱增强视图进行有监督学习，优化交叉熵损失。
- 通过预测层（Cls Head），计算交叉熵损失： $\ell_{sup}=\frac{1}{B} \sum_{i=1}^{B} \mathrm{H}\left(y_{i}, P_{{cls}}\left( Aug_{w}\left(x_{i}\right)\right)\right)$
- 输入： $\mathcal{X}=\left\{\left(x_{i}, y_{i}\right): i \in(1, \ldots, B)\right\}$ ，其中 $x_{i}$ 为第 $i$ 张图片， $y_{i}$ 为该图片对应的 $one-hot$ 向量， $B$ 为采样的一个批量大小。
- 输出： $p_{m}\left ( y|x \right )$ ，模型对输入 $x$ 产生的预测类别分布。

类感知对比半监督学习(Class-Aware Contrastive Semi-Supervised Learning)论文阅读笔记 — 图1 CCSSL架构。给定一个批次的无标记图像，弱增强视图经过半监督模块，该模块可以采用任意的基于伪标签的半监督学习方法来产生模型预测结果。

对于无标签样本：
- 输入： $\mathcal{U}=\left\{u_{i}: i \in(1, \ldots, \mu B)\right\}$ ，其中 $\mu$ 是一个超参数，权衡有标签样本集 $\mathcal{X}$ 和无标签样本集 $\mathcal{U}$ 的相对大小。对于一张图片，生成一个弱增强视图 $Aug_{w}\left ( \cdot \right )$ 和两个强增强视图 $Aug_{s1}\left ( \cdot \right )$ 和 $Aug_{s2}\left ( \cdot \right )$ ，其中 $Aug_{w}\left ( \cdot \right )$ 和 $Aug_{s1}\left ( \cdot \right )$ 经过预测层（Cls Head）， $Aug_{s1}\left ( \cdot \right )$ 和 $Aug_{s2}\left ( \cdot \right )$ 经过投影层（Proj Head）。
- 输出：投影层（Proj Head）为2层线性层，将高维特征表示映射为低维嵌入向量；预测层（Cls Head）为1层线性层，在训练期间生成伪标签，并在推理时输出预测分布。
如图1所示，架构主要分为两个模块：
- 类感知对比模块：投影层最后一层输出维度为维特征向量，图片的两个强增强视图和经过投影层（Proj Head）分别得到和的N维特征向量。
  - 采用 $T_{p u s h}$ 阈值判断样本为分布内数据还是分布外数据。对于分布内数据为 $\max (p)\geq T_{p u s h}$ ，采用有监督对比学习进行聚类；对于分布外数据 $\max (p)< T_{p u s h}$ ，采用无监督对比学习进行优化。
  - 有监督对比矩阵（Supervised Contrastive Matrix）：根据伪标签，若 $z_{i}$ 和 $z_{j}$ 来自同一类别，则视为正样本对，不同类别的嵌入向量视为负样本对。
  - 类感知对比矩阵（Class-Aware Contrastive Matrix）：与锚点具有相同类别的、且最大预测概率分量大于 $T_{p u s h}$ 的嵌入向量作为正样本，不同类别的、或最大预测概率分量小于 $T_{p u s h}$ 的视图作为负样本。
  - 权重配置模块（Re-weighting）：将学习重点放在高置信度的干净数据上，对类感知对比矩阵进行加权，加权规则：①同一嵌入向量与其本身对比，权重为1；②嵌入向量与其他嵌入向量对比，权重为关于两个嵌入向量对应的图片的弱增强视图 $Aug_{w}\left ( \cdot \right )$ 经过预测层（Cls Head）得到最大预测概率分量的乘积。
  - 目标矩阵（Target Matrix）：对类感知对比矩阵进行权重配置后得到的矩阵即为目标矩阵。
  - 相似性矩阵（Feature Affinity）：两个强增强视图 $Aug_{s1}\left ( \cdot \right )$ 和 $Aug_{s2}\left ( \cdot \right )$ 经过投影层，构造得到 $2N\times 2N$ 的特征矩阵。
- 半监督模块：
  - 损失函数计算：
    - 高于阈值的具有高置信度的伪标签与强增强样本 $Aug_{s1}\left ( \cdot \right )$ 得到的预测分布 → 计算交叉熵损失： $\mathcal{L}_{u}=\frac{1}{\mu B} \sum_{i=1}^{\mu B} \mathbb{1}\left(\max \left(p_{i}\right) \geq t\right) H\left(\hat{q}_{i}, P_{c l s}\left(A u g_{s}\left(u_{i}\right)\right)\right )$
  - 半监督模块可替换为任意基于伪标签的半监督学习方法，如FixMatch、MixMatch、CoMatch等生成伪标签的策略。论文里基于FixMatch进行结果展示。

4 损失函数

4.1自监督对比学习损失函数（Self-Supervised Contrastive Loss）

对于大小为 $N$ 的小批量，随机采样的样本对集合（记为 $\left\{\boldsymbol{x}_{k}, \boldsymbol{y}_{k}\right\}_{k=1 \ldots N}$ ），通过不同的数据增强方法为每个样本两个视图，因此共得到 $2N$ 个视图样本对（记为 $\left\{\tilde{\boldsymbol{x}}_{\ell}, \tilde{\boldsymbol{y}}_{\ell}\right\}_{ \ell=1 \ldots 2 N}$ ）。

$\mathcal{L}^{\text {self }}=\sum_{i \in I} \mathcal{L}_{i}^{\text {self }}=-\sum_{i \in I} \log \frac{\exp \left(\boldsymbol{z}_{i} \cdot \boldsymbol{z}_{j(i)} / \tau\right)}{\sum_{a \in A(i)} \exp \left(\boldsymbol{z}_{i} \cdot \boldsymbol{z}_{a} / \tau\right)}=\sum_{i \in I} \left(\log\sum_{a \in A(i)} \exp \left(\boldsymbol{z}_{i} \cdot \boldsymbol{z}_{a} / \tau\right) - \log\exp \left(\boldsymbol{z}_{i} \cdot \boldsymbol{z}_{j(i)} / \tau\right)\right)$

前者表示锚点与 $2N-2$ 个负样本的相似性，后者表示锚点与正样本的相似性。优化loss函数等同于减小前者（拉远负样本）和增大后者（拉近正样本）.

其中：

$i \in I \equiv\{1 \ldots 2 N\}$ 为任意视图的索引（ $i$ 也称为锚点）
$j\left ( i \right )$ 表示来自相同样本的除了视图 $i$ 以外的另一视图的索引（ $j \left ( i \right )$ 也称为正样本，共1个正样本对）
$A\left ( i \right )$ 表示除了索引 $i$ 以外的其他视图的索引，共有 $2N-1$ 个索引
$\boldsymbol{z}_{i}$ 表示索引为 $i$ 的视图经过投影层输出的特征表示，假设投影层输出为128维度，则 $\boldsymbol{z}_{i}$ 维度为 $\left [ N,128 \right ]$ ， $\boldsymbol{z}_{i}$ 点乘 $\boldsymbol{z}_{j(i)}$ 的转置，得到的结果矩阵特征维度为 $\left [ N,128 \right ]\cdot \left [ 128,N \right ] = \left [ N,N \right ]$
$\tau$ 为温度系数，是一个正整数，是控制困难负样本惩罚强度的关键参数

4.2 有监督对比学习损失函数（Supervised Contrastive Loss）

对于大小为 $N$ 的小批量，随机采样的样本对集合（记为 $\left\{\boldsymbol{x}_{k}, \boldsymbol{y}_{k}\right\}_{k=1 \ldots N}$ ）， $x_{k}$ 是一个图片实例， $y_{k} \in \mathbb{R}^{K}$ ， $K$ 表示类别数量。

$\mathcal{L}_{\text {con }}^{sup}=-\frac{1}{N} \sum_{i=1}^{N} \frac{1}{\left|P\left ( i \right ) \right|} \sum_{j \in P\left ( i \right ) } \log \frac{\exp ^{\left(z_{i}\cdot z_{j} / \tau\right)}}{\sum_{a \in A\left ( i \right ) } \exp ^{\left(z_{i}\cdot z_{a} / \tau\right)}}$

其中：

$i \in I \equiv\{1 \ldots N\}$ 为任意图片的索引（ $i$ 也称为锚点）
$j$ 表示具有相同类别标签的、除了图片 $i$ 以外的其他全部图片的索引（ $j$ 也称为正样本）
$P\left ( i \right )$ 包含了所有的正样本对索引， $\left | P\left ( i \right ) \right |$ 为批量中与锚点具有相同类别标签的图片数量（不包括锚点）
$A\left ( i \right )$ 表示除了索引 $i$ 以外的其他图片的索引，共有 $N-1$ 个索引
$\boldsymbol{z}_{i}$ 表示索引为 $i$ 的图片经过投影层输出的特征表示，假设投影层输出为128维度，则 $\boldsymbol{z}_{i}$ 维度为 $\left [ N,128 \right ]$ ， $\boldsymbol{z}_{i}$ 点乘 $\boldsymbol z_{j}$ 的转置，得到的结果矩阵特征维度为 $\left [ N,128 \right ]\cdot \left [ 128,N \right ] = \left [ N,N \right ]$
$\tau$ 为温度系数，是一个正整数，是控制困难负样本惩罚强度的关键参数

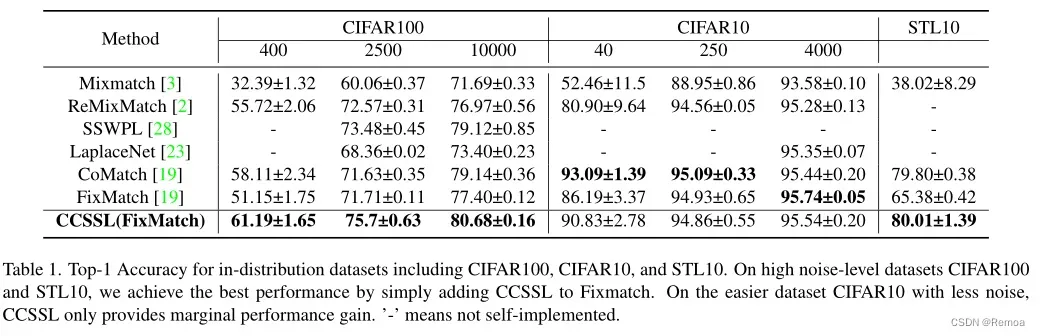
5 模型性能

超参数配置

实验超参数配置（参考github中代码实现）
超参数	CIFAR0-10	CIFAR-100	Semi-iNat 2021
总迭代次数 iterations	512 epochs * 1024 iterations / epoch	512 epochs * 1024 iterations / epoch	512 epochs * 1024 iterations / epoch
输入图像大小	32 X 32	32 X 32	224 X 224
批量大小 bactch_size	64（代码中实现为16 * 4 gpus的多GPU配置，右同）	64	64
主干网络 backbone	Wide-ResNet-28-2	Wide-ResNet-28-8	ResNet-50
伪标签阈值 $\tau$	0.95	0.95	0.8
分布内外数据判定阈值 $T_{push}$	0	0	0.9
有标记和无标记样本相对大小系数 $\mu$	7	7	7
半监督损失权衡因子 $\lambda_{u}$	1.0	1.0	1.0
类感知对比损失权衡因子 $\lambda_{c}$	0.2	1.0	2.0
学习率 learning_rate	0.03	0.03	0.03
学习策略 learning_rate_schedule	cosine decay	cosine decay	cosine decay
对比损失温度系数 $T$	0.07	0.07	0.07
权重衰减 weight_decay_factor	0.0005	0.001	0.001
动量 momentum_factor	0.9	0.9	0.9
是否使用Nesterov加速	True	True	True
是否采用ema指数移动平均 ema	True	True	True
分类层输入维度 classification_input_dimension	128	512	2048
分类层输出维度 classification_output_dimension	10	100	810
投影层输入维度 projection_input_dimension	128	512	2048
投影层输出维度 projection_output_dimension	64	64	64
投影层深度 projection_depth	2	2	2

参考文献

[1]Berthelot D, Carlini N, Goodfellow I, et al. Mixmatch: A holistic approach to semi-supervised learning[J]. Advances in Neural Information Processing Systems, 2019, 32.

[2]Sohn K, Berthelot D, Carlini N, et al. Fixmatch: Simplifying semi-supervised learning with consistency and confidence[J]. Advances in Neural Information Processing Systems, 2020, 33: 596-608.

[3]Yang F, Wu K, Zhang S, et al. Class-Aware Contrastive Semi-Supervised Learning[J]. arXiv preprint arXiv:2203.02261, 2022.

文章出处登录后可见！

已经登录？立即刷新

类感知对比半监督学习(Class-Aware Contrastive Semi-Supervised Learning)论文阅读笔记