原文标题 ：An Illustrated Explanation of Hypothesis Tests

假设检验的图解说明

一劳永逸地了解什么是假设检验。 Python 中的代码。

免责声明：嘿，为了清楚起见，这不是赞助帖子。我真的很喜欢这本书。

Hypothesis Test

我最近读了这本很好的书《统计学的卡通导论》。它为基本的统计概念带来了有趣而流畅的介绍，所有这些都像漫画书一样呈现。[0]

引起我注意的一点，也是我今天要揭示的，是作者 Grady Klein 如何解释假设检验的概念。用他的话说……

假设检验是猜测总体平均值并将该猜测与我们已经拥有的样本中的平均值进行比较的奇特名称。

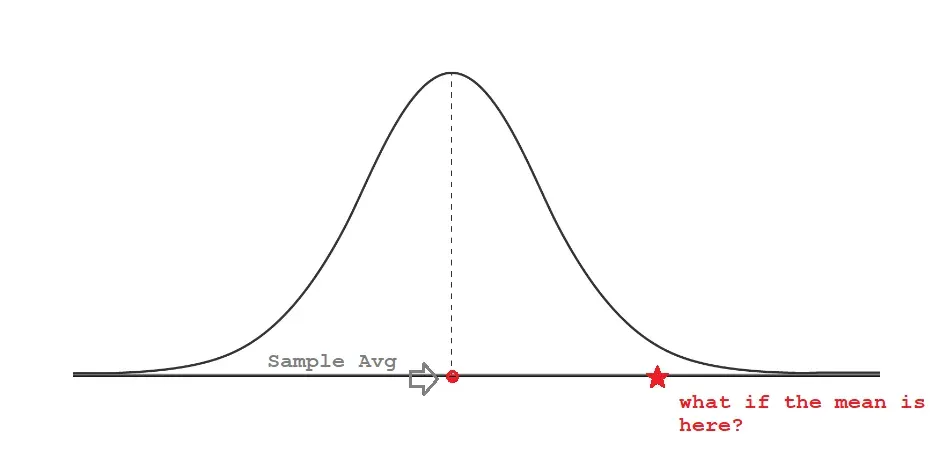
现在假设我们收集了另一个样本，但我们不知道该样本是否来自我们的分布。我们能做什么？我们通过计算在“星”点上具有平均值的样本与在“圆”点。

在我们的测试中，除非另有证明，否则每个人都是无辜的。意思是，测试将假设样本 1 和样本 2 来自同一总体，并将该假设称为零假设 (Ho)。但如果我们错了，他们不是来自同一个群体，这个假设被称为替代假设（Ha）。

让我们确定测试的阈值。在这种情况下，5% 是经验法则。如果两个样本来自同一总体的概率（p 值）小于 5%，那么我们可能错了，所以我们有强有力的证据拒绝 Ho。但是如果我们的 p 值高于 5%，我们的机会表明我们没有足够的证据来拒绝 Ho，所以我们保持样本来自同一总体的假设。也许这只是一个具有奇怪平均值的奇怪样本。

# Imports
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import f_oneway
from statsmodels.stats.weightstats import ztest# Create df
df = pd.DataFrame({'id': np.arange(1,51),'val': np.random.randn(50)})# Mean
df.val.mean()
[OUT] -0.054089553629615886#----# Create df2
df2 = pd.DataFrame({'id': np.arange(1,51),
'val': np.random.randint(40,50, size=50)/10})# Mean 2
df2.val.mean()
[OUT] 4.513333333333334# Test
"Can a distribution with mean sample 2 come from the same population as sample 1?
Ho : p-value >= 0.05 == Yes, same population
Ha : p-value < 0.05 == No, different population"
sample1 = df.val
mean_sample2 = df2.val.mean()# Z-test
stat, p = ztest(sample1, value=mean_sample2)
print(f'Test statistics: {stat}')
print(f'p-Value: {p}')[OUT]
Test statistics: -26.21106515561983 p-Value: 1.9876587424280803e-151

正如我们所看到的，原假设 (Ho) 被拒绝，因此我们有强有力的证据可以得出结论，两个样本都来自不同的群体。
在实践中，这意味着，如果我们认为真实的总体平均值为 -0.054（与样本 1 相同），那么找到平均值为 4.51 的样本将非常非常非常不可能。实际上，它被发现的机会几乎为零。

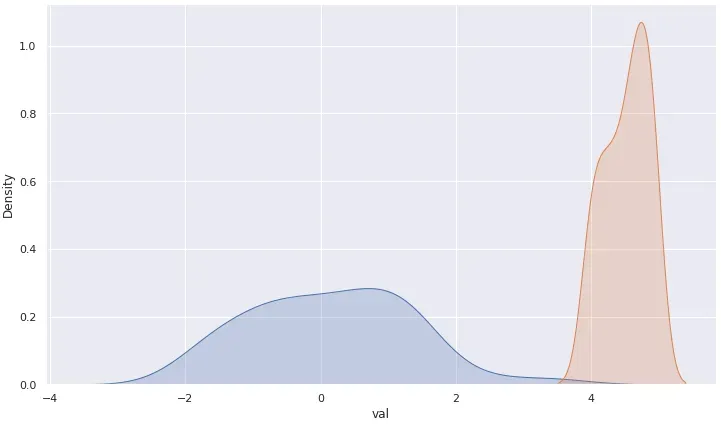
来自同一人群

让我们尝试另一个测试。现在我将实际从样本 1 中提取样本 3 并测试它们来自同一总体的概率是否正确。

# Create df3
df3 = pd.DataFrame({'id': np.arange(1,31),'val': np.random.choice(df['val'].values, size=30)})# Mean 3
df3.val.mean()
[OUT] 0.04843756603887838

酷，平均值更接近样本 1 平均值 (-0.054)。这是一个好兆头。

sample1 = df.val
mean_sample3 = df3.val.mean()stat, p = ztest(sample1, value=mean_sample3)
print(f'Test statistics: {stat}')
print(f'p-Value: {p}')[OUT] 
Test statistics: -0.3488669147011808 p-Value: 0.727189224747824

哇！这两个随机正态样本来自同一群体的概率为 72%。那讲得通。 3是从1中提取的！

# Plot
sns.kdeplot(data=df, x='val', fill=True)
sns.kdeplot(data=df3, x='val', fill=True)
plt.legend(['Sample1', 'Sample3']);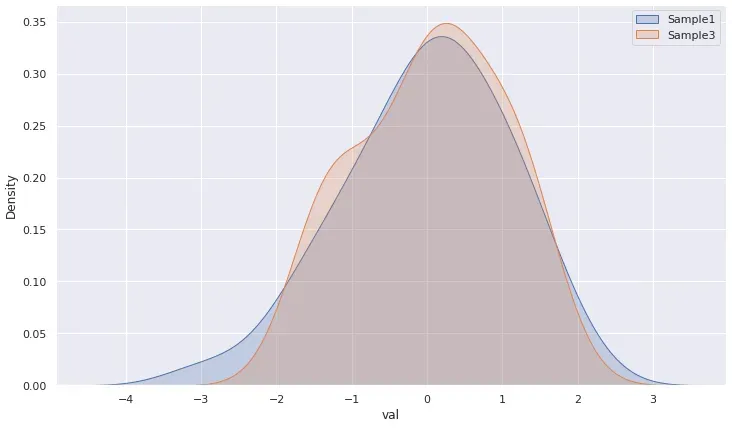

Before You Go

我想创建这篇快速帖子，向您展示假设检验背后的内容。我们实际测试的是什么。这就是这里的目标，所以你可以围绕这个重要的统计概念建立你的直觉。

我们有一个平均值为 -0.05 的样本
我们有一个样本 2，平均值为 4.51
假设检验：考虑到真实的总体平均值为 -0.05 或非常接近，两个样本是否可能来自同一个总体？
我们开始假设是的，他们来自同一人群。然后我们计算 p 值或概率值。
如果它小于 5% 的机会，我们拒绝它而支持 Ha，说统计证据表明这两个样本来自不同的分布。如果超过 5%，那么我们没有统计证据表明他们不是来自同一人群，因此我们假设他们是。

GitHub代码：https://tinyurl.com/3csp5ejm[0]

如果您喜欢此内容，请关注我的博客以获取更多信息。

文章出处登录后可见！

已经登录？立即刷新