目标检测的预测框回归损失函数由Classificition Loss和Bounding Box Regeression Loss两部分构成,本文介绍Bounding Box Regeression Loss。
1. L1 loss
L1 loss也称为平均绝对误差,即真实值和预测值差值的绝对值:
设y-f(x)为横轴,MAE值为纵轴,函数图像如下:
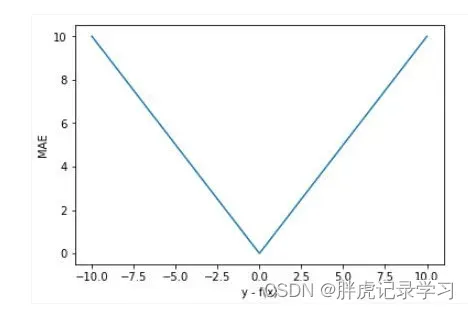
由图可知,L1损失函数对y-f(x)的导数为常数,在训练后期,即y与f(x)接近时,也即y-f(x)很小时,假设learning rate不变,损失函数会在稳定值附近波动,由于梯度的稳定,不利于模型收敛,很难收敛到更高的精度。
2. L2 loss
L2 loss也称为均方误差,即真实值和预测值差值的平方:
设y-f(x)为横轴,MSE值为纵轴,函数图像如下:
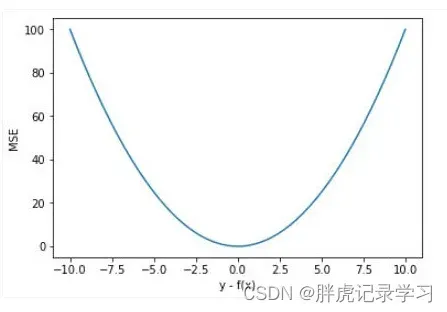
由图可知,L2 loss函数处处可导,由于存在平方运算,当损失值大于1时,误差将会被放大;损失小于1时,误差将会被缩小,L2损失函数对y-f(x)的导数在y-f(x)值很大时,其导数也非常大,在训练前期不稳定,会造成模型的最终效果不太好。
3. smooth L1 loss
总结上述两种loss的缺点,smooth L1 loss改善L1 loss中的不可导点和梯度过于稳定的情况以及L2 loss中y-f(x)过大时梯度也很大的问题:
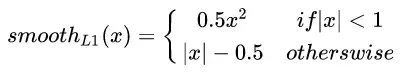
其中,为真实值与预测值的差值,Smooth L1对x的导数为:
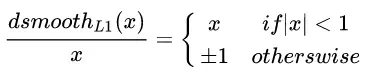
实际使用时:
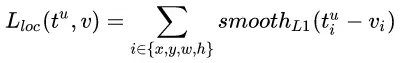
其中,表示真实框坐标,
表示预测的框坐标,即分别求出4个点的loss然后相加作为Bounding Box Regression Loss;
L1、L2、smooth l1三者的函数图像如下:
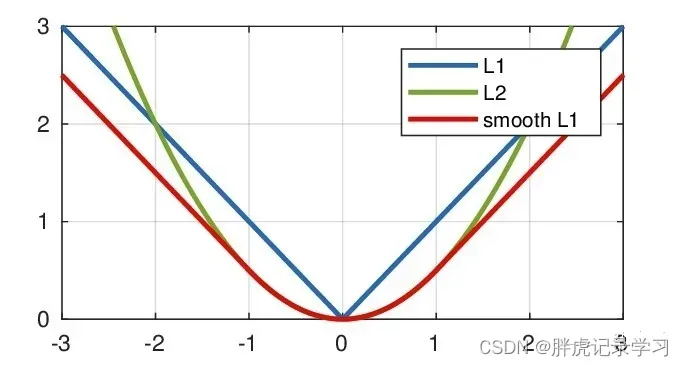
由图可知,smooth L1分别继承了L1和L2的优点:在损失大即当预测框与ground truth差别过大时的情况下,梯度不至于太大,损失小即当预测框与ground truth差别过小时的情况下,梯度足够小, 相比于L1损失函数,smooth L1可以收敛得更快,相比于L2损失函数,smooth L1对离散点、异常值不敏感,梯度变化相对更小;
Smooth L1 Loss在计算目标检测的bbox loss时,都是独立的求出4个点的loss然后相加得到最终的bbox loss,即默认4个点是相互独立的,假设坐标之间是没有相关性的,这与实际情况不符,例如当(x,y)位于图片右上角时,此时w=0,h=c。
4. IoU loss
论文地址:
《UnitBox: An Advanced Object Detection Network (ACM-MM2016)》
针对Smooth L1没有考虑box四个坐标之间相关性的缺点:
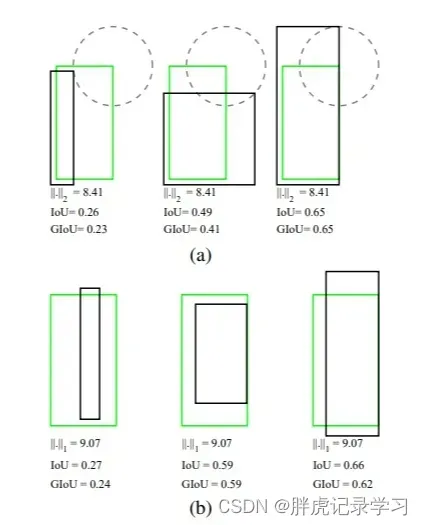
图(a)中的L2损失值都是8.41,但是具有不同的IoU,图b中的L1损失值都是9.07,同样具有不同的IoU,可以得出,L1与L2的loss并不能衡量回归任务,不能等价于最后用于评测目标检测指标的IoU;
通过4个坐标来回归框并没有引入box四个顶点之间的相关性,IoU loss将4个坐标当作一个整体进行回归,IoU Loss的定义是先求出预测框和真实框之间的交集和并集之比,再求负对数,但是在实际使用中我们常常将IoU Loss写成1-IoU。如果两个框重合则交并比等于1,Loss为0说明重合度非常高,IoU满足非负性、同一性、对称性、三角不等性,相比于L1、L2等损失函数还具有尺度不变性,不论box的尺度大小,输出的IoU损失总是在0-1之间,所以能够较好的反映预测框与真实框的检测效果:
IoU loss定义如下,IoU Loss在设计损失时为规范化的坐标值/尺度建立了联系,可以直接反映预测框的检测效果,同时IoU对尺度也不敏感:
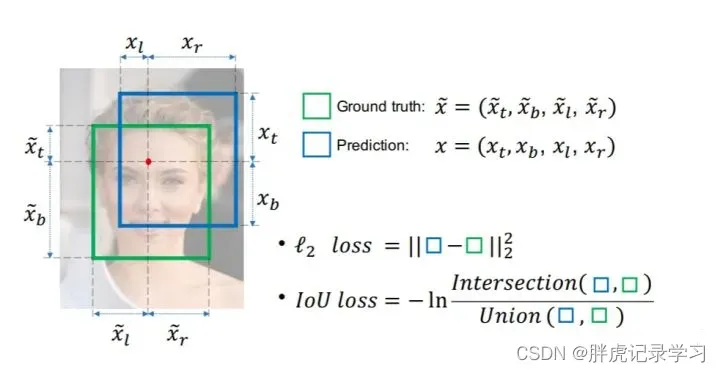
上图中的红色点表示目标检测网络结构中Head部分上的点(i,j),绿色的框表示Ground truth框, 蓝色的框表示Prediction的框,IoU loss的定义如上,先求出2个框的IoU,然后实际使用时IoU Loss =1-IoU;
伪代码如下:

其中,X是预测Bounding box的面积,是真实Bounding box的面积,I是两个区域的交集,U是两个区域的并集,L是对IOU的交叉熵损失函数;
IoU Loss 缺点:
IOU Loss虽然解决了Smooth L1系列变量相互独立和不具有尺度不变性的两大问题,但是当预测框和目标框不相交,当IoU(A,B)=0时,不能反映两个框距离的远近,此时损失函数不可导,IoU loss无法优化两个框不相交的情况,根据IOU loss等于0,没有梯度的回传无法进一步学习训练;
假设预测框和目标框的大小都确定,只要两个框的相交值是确定的,其IoU值是相同时,IoU值不能反映两个框是如何相交的,如下图所示:
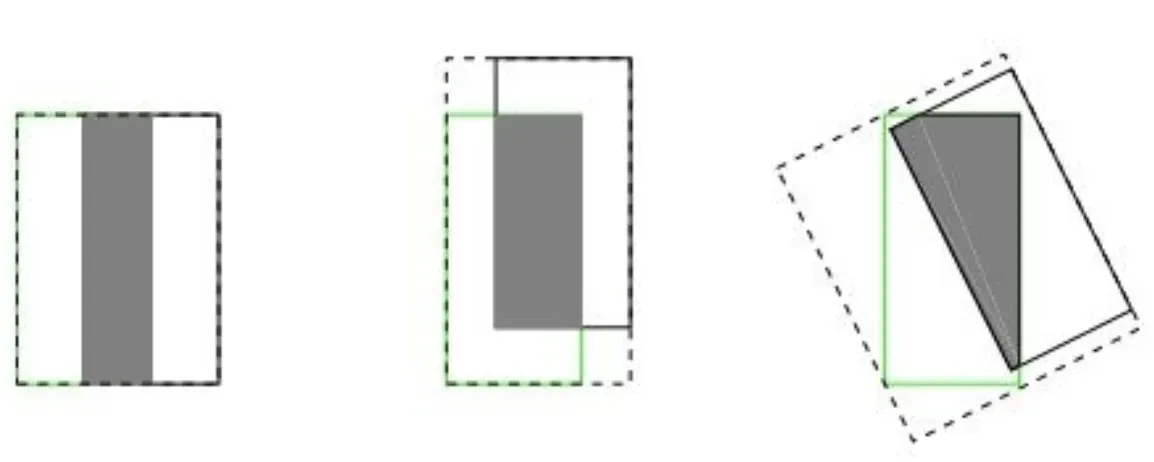
如上图所示,三种不同相对位置的框拥有相同的值IoU=0.33,但IoU值不能反映两个框是如何相交的,但直观上判断回归的效果是:左>中>右;
5. GIoU loss
论文地址:
《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression (CVPR2019)》
为解决上述IoU loss的问题,有学者提出了GIoU loss:
其中,是两个框之间的最小闭包框面积,即能同时包含两个框的最小框面积;
当时,表明两个框不重叠,且GIoU越小,两框的距离越远,
时表明相距无穷远;
当时,表明两个框重叠,且GIoU越大,两框的重合程度越好,
时表明完全重合;
GIoU取值范围为 [-1, 1],在两框重合时取最大值1,在两框无限远的时候取最小值-1,同时与IoU只关注重叠区域不同,GIoU不仅关注重叠区域,还关注其他的非重合区域,能更好的反映两者的重合度;
伪代码如下:

其中C为包含A和B的外接矩形,用C减去A和B的并集除以C得到一个数值,然后再用框A和B的IoU减去这个数值即可得到GIoU的值;
GIoU采用距离度量损失函数,并且对尺度不敏感,依旧对具体的坐标值/尺度不敏感,上图中的GIoU(从左到右):0.33,0.24,-0.1,其GIoU值同时反映了重叠方式。
GIoU Loss 缺点:
当真实框完全包裹预测框的时候,IoU和GIoU的值都一样,此时GIoU退化为IoU, 无法区分其相对位置关系,GIoU在考虑不重叠的情况时,只度量了距离却忽视了框的尺度:
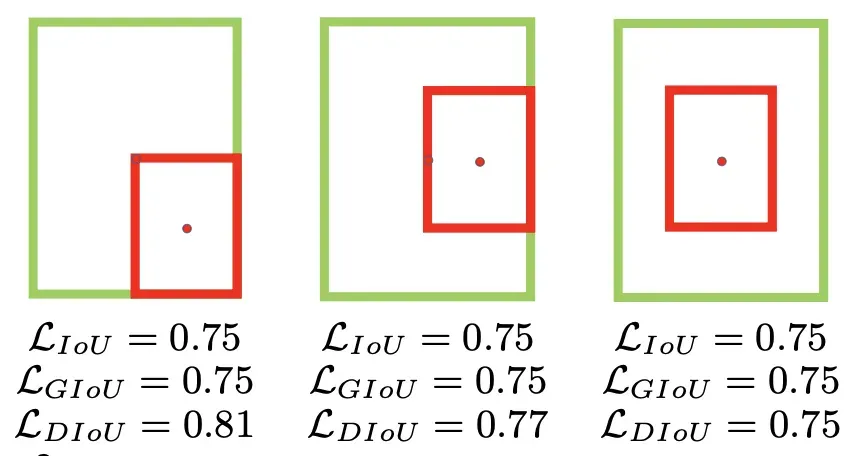
GIoU Loss相同,但直觉上显然第三种情况回归更好;
6. DIoU Loss
论文地址:
《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression (AAAI2020)》
针对上述GIoU的问题,即预测框和真实框是包含关系的情况或者处于水平/垂直方向上,GIoU损失几乎已退化为IoU损失,导致收敛较慢,有学者将GIOU中引入最小外接框来最大化重叠面积的惩罚项修改成最小化两个BBox中心点的标准化距离从而加速损失的收敛过程;
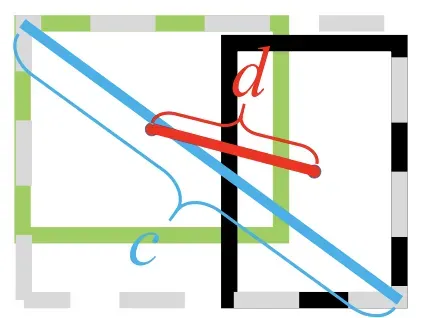
其中,绿色框为真实框,黑色框为预测框,灰色框为两者的最小外界矩形框,b和分别是预测框和真实框的中心点,
度量了两点之间的欧式距离,c是预测框和真实框的最小闭包框的对角线距离;
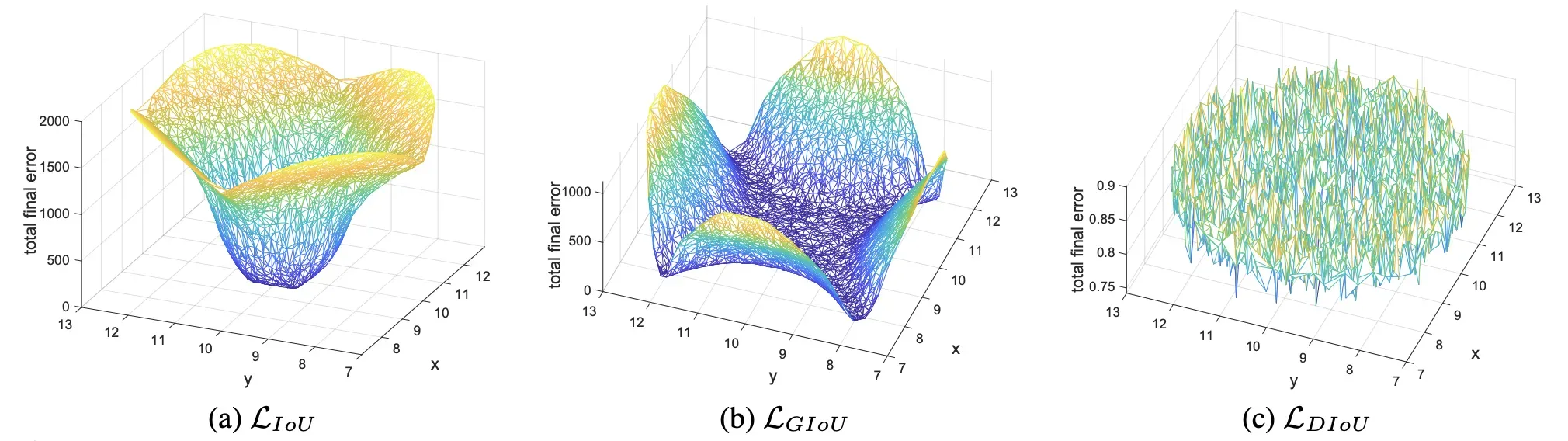
DIoU跟GIoU一样,能在两框不重叠时为训练提供方向,DIoU在两框不重叠时既考虑了距离,也考虑了尺度,在两框处于水平或垂直方向上时,DIoU依旧能为训练网络做出不错的贡献,DIoU直接最小化两框的距离,拥有更加平滑的损失曲面,因此收敛比GIoU更快;
7. CIoU Loss
论文地址:
《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression (AAAI2020)》
在DIoU Loss的基础上,论文继续引入长宽比的惩罚得到CIoU Loss,惩罚项公式如下:
其中是用于做trade-off的参数:
v是用来衡量长宽比一致性的参数,,完全相等时v=0:
完整的CIoU损失函数:
然而在CIoU的定义中,衡量长宽比过于复杂,从以下两个方面减缓了收敛速度:
长宽比不能取代单独的长宽,比如、
都会导致v=0;
从v的导数可以得到,说明
和
在优化时意义相反;
8. EIoU Loss
论文地址:
《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》
解决CIoU定义中的不足,引入了解决样本不平衡问题的Focal Loss思想,将CIoU的取代为
EIoU Loss的定义为:
9. 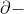 IoU loss
IoU loss
论文地址:
《Alpha-IoU: A Family of Power Intersection over Union Losses for Bounding Box Regression》
将现有的基于IoU的Loss推广到一个新的PowerIoU系列的Loss,它具有一个幂次IoU项和一个附加的幂次正则项,可以显著的超过现有的基于IoU的损失,通过调节α,使探测器更灵活地实现不同水平的bbox回归精度,对小数据集和噪声的鲁棒性更强;
并且通过实验发现,在大多数情况下,取α=3的效果最好。
10. SIoU loss
论文地址:
《SIoU Loss: More Powerful Learning for Bounding Box Regression》
好的目标框回归损失应该考虑三个重要的几何因素:重叠面积,中心点距离,长宽比;还应该考虑真实框与期望框不匹配的方向,所以提出了一个新的损失函数SIoU,其中惩罚度量被重新定义考虑中心点向量之间的期望角度回归;
SIoU损失函数由4个cost函数组成:
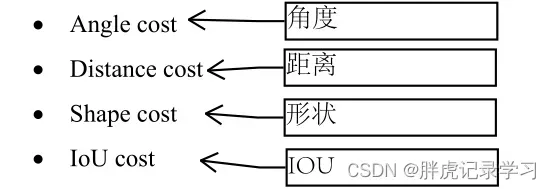
将角度成本贡献转化为损失函数,收敛的过程首先尽量最小化 if
,
, others:
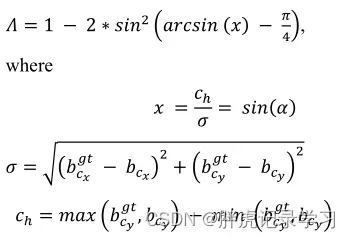
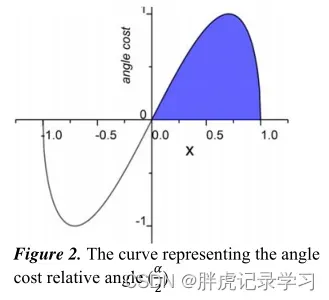
angle cost结果:
距离cost:

形状cost:
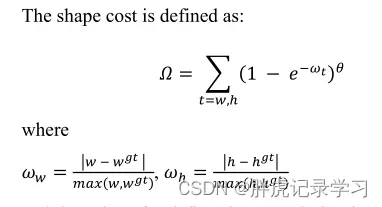
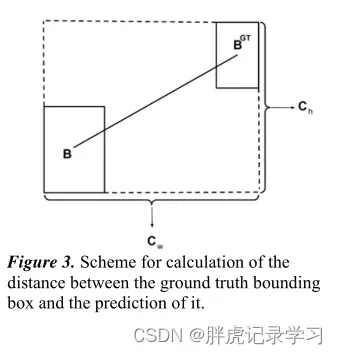
loss function:

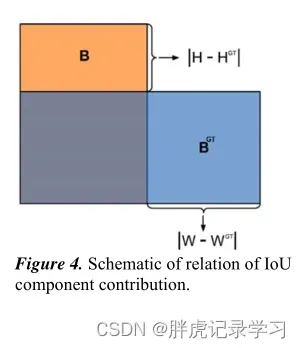
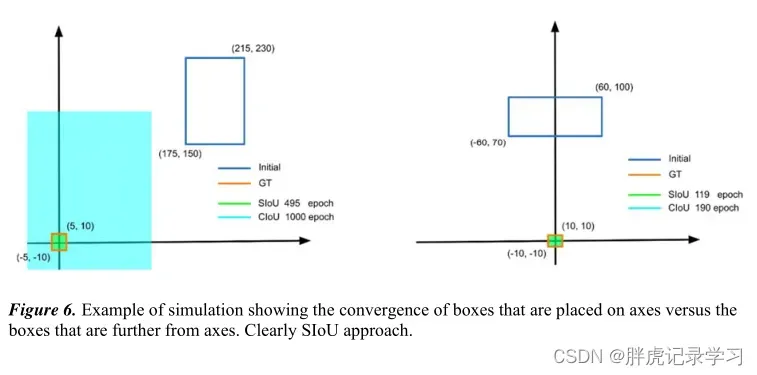
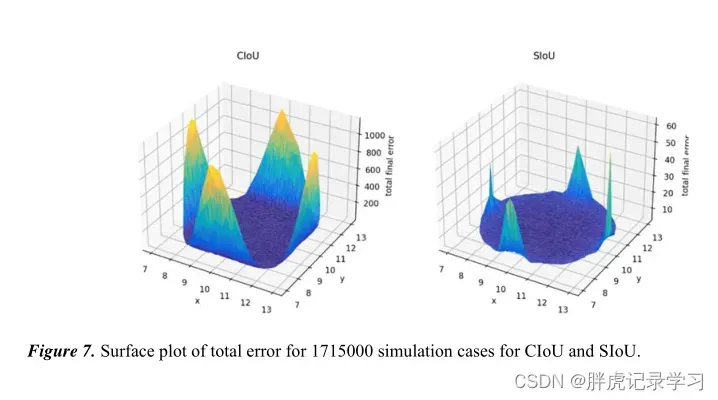
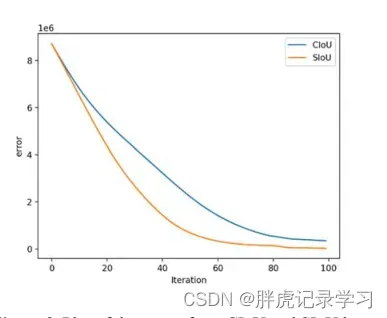
实验结果:
参考:
仅为学习记录,侵删!
文章出处登录后可见!
