提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

前言

这学期上了一门数值计算课程，老师要求用程序实现拉格朗日插值以及牛顿插值，并验证Runge现象，参照网上相关资料后，用python完成两种插值计算以及输出曲线图。

一、多项式插值

插值法又称“内插法”，是利用函数f (x)在某区间中已知的若干点的函数值，作出适当的特定函数，在区间的其他点上用这特定函数的值作为函数f (x)的近似值，这种方法称为插值法。如果这特定函数是多项式，就称它为多项式插值。常用的几种多项式插值法有：直接法、拉格朗日插值法和牛顿插值法。

二、Python计算以及曲线图

1.拉格朗日插值

这是在网上查阅到的源码，原文链接：版权归原作者所有，转载需注明。

import numpy as np
import matplotlib.pyplot as plt

X = input("x的值：").split(' ')
Y = input("y的值：").split(' ')
x = input("要预测的值：")
print('\n')

X = np.array(X).astype(np.float64)
Y = np.array(Y).astype(np.float64)
x = np.array(x).astype(np.float64)

n = len(X)

# 原函数
def fun(x):
 return np.sin(x)

# 累乘函数
def T(x, i, X):
 T_i = 1
 for x_i in X:
  if X[i] == x_i:
   continue
  T_i = T_i * (x-x_i)
 return T_i

# 插值基函数
def P(i, x, X, Y):
 P_i = T(x, i, X)/T(X[i], i, X) * Y[i]
 return P_i

# 计算预测值
def L(x, X, Y):
 result = 0
 for i in range(n):
  result = result + P(i, x, X, Y)
 return result

y = L(x, X, Y) 
  
print("预测结果：" + str(y) + '\n')
print("误差：" + str(fun(x) - y))

# 画图
X_n = np.linspace(0, 1, 50)
Y_n = fun(X_n)

x_n = np.linspace(0, 1, 50)
y_n = L(x_n, X, Y)

l1, = plt.plot(X_n, Y_n, label='theory')
l2, = plt.plot(x_n, y_n, label='prediction',linestyle='--')
plt.legend(handles=[l1,l2,],labels=['theory','prediction'], loc='best')

plt.show()

在此基础，对源码进行了部分修改，将计算部分整合成一个函数，其中X,Y为输入的点，x为待计算的值

def lagrange(X,Y,x):
    ans=0.0
    for i in range(len(Y)):
        t=Y[i]
        for j in range(len(Y)):
            if i!=j:
                t*=(x-X[j])/(X[i]-X[j])
        ans+=t
    return ans

2.牛顿插值

基于以上的程序，我们只需要修改插值计算部分，其中x,y为输入的点，u为待计算的值

def newton(x,y,u):
#差商计算
    c=np.zeros((n,n))
    for i in range(n):
        c[i,0]=y[i]
    for i in range(1,n):
        for j in range(i,n):
            c[j,i]=(c[j,i-1]-c[j-1,i-1])/(x[j]-x[j-i])
#预测值s
    s=y[0]
    for i in range(1,n):
        t=1
        for j in range(0,i):
            t*=(u-x[j])
        s+=c[i,i]*t
    
    return s

三、结果分析

1.拉格朗日插值

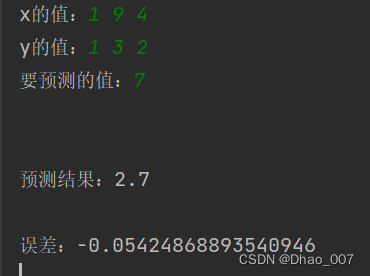
我这里输入的点为（1,1）（9,3）（4,2），原函数设置为f(x)=x^0.5，要预测的值为7，也就是用多项式函数g(x)估算根号7的值，输出曲线图如下：

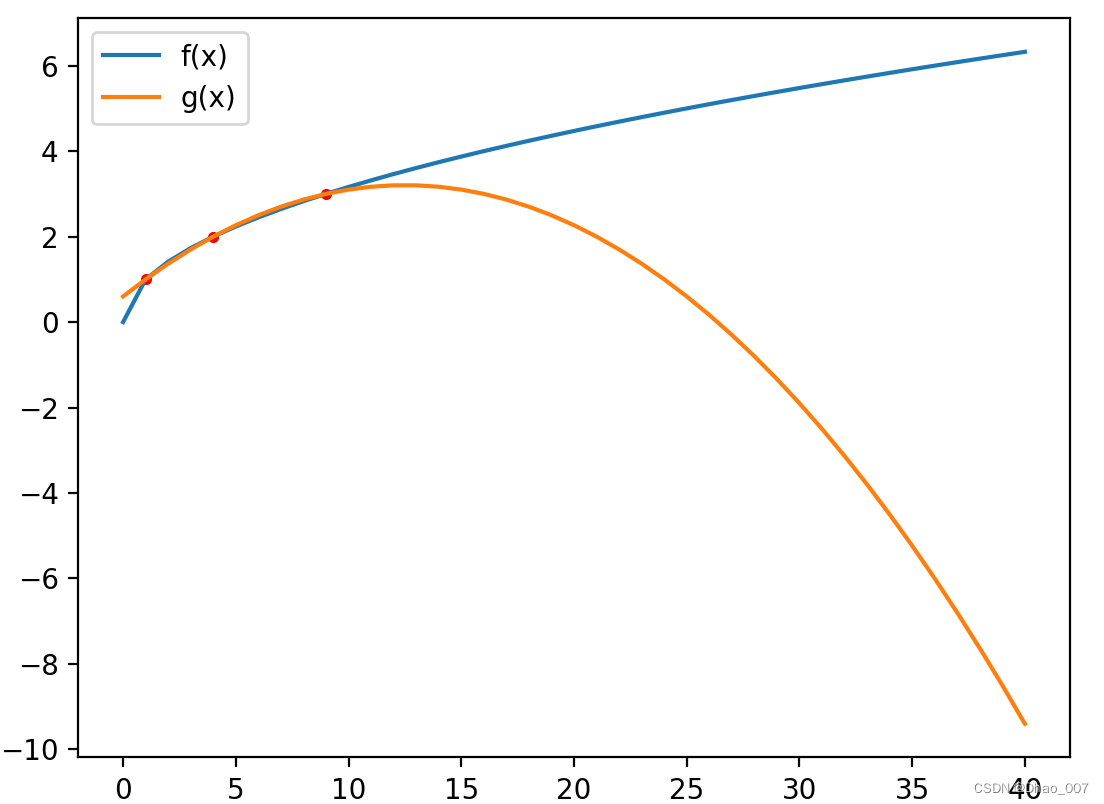
2.牛顿插值

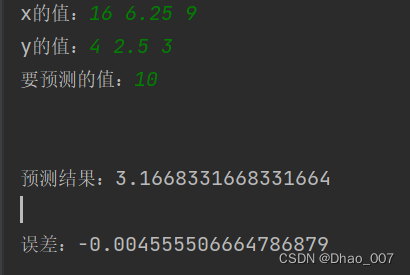
我这里输入的点为（16,4）（6.25,2.5）（9,3），要预测的值为10，输出曲线图如下：

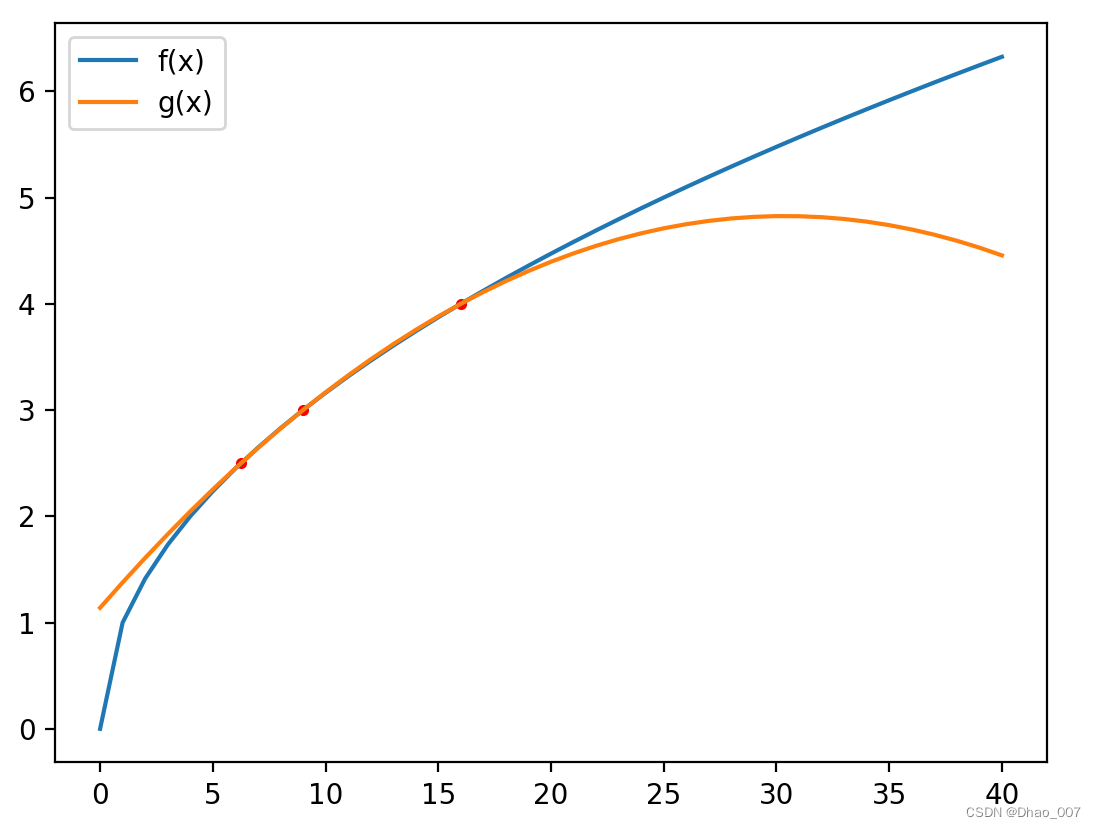
总结

插值原理部分没有写，在网上有挺多博主讲解，写本文主要目的完成作业后无聊记录一下，源代码哪里不理解的可以留言多多交流。如需整份源码，留言即可，我看到后会尽快回复。大家一起加油，好好学习天天向上。