深入理解PSNR
作者:老李
日期:2022-1-19
本文引入MSE、SNR、变异系数(Coefficient of Variation),并希望从统计学的角度上解释这个变量
这个变量。
PSNR是“Peak Signal to Noise Ratio”的缩写,即峰值信噪比。
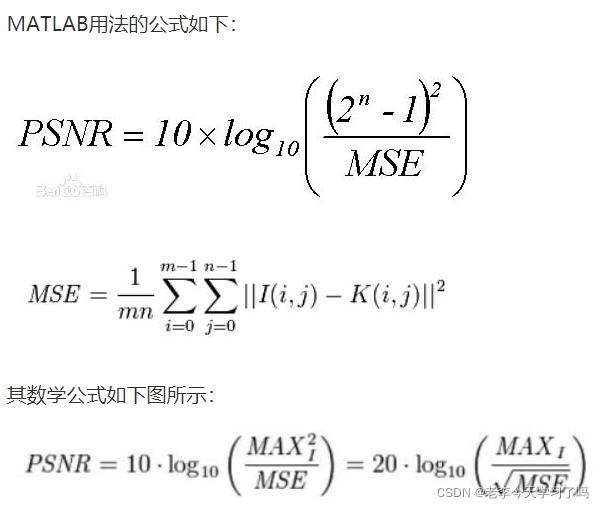
MSE
用 真实值-预测值 然后平方之后求和平均。
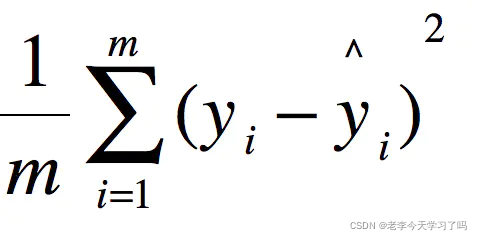
在图像中的MSE定义说人话就是:
两个图像中每一个相同位置的像素值相减,平方,求和,再求平均。
表达的是两幅图在每一个位置上的像素值的差异的平均。
数值越大,表示两张图片在相似度上更低。
这里注意两点:
- 在计算之前要把两个图像调整为同一个阈值,一个[0,1]和一个[0,255]是不能放一起用的。
- 图像的大小要保持一致。不然无法做到像素值之间的一一对应。
MSE在描述两图像的相似成都时具有它的局限性。
其中一点是这个定义太简单了,不一定完全符合视觉上规律。
比如说如果两图像是少量的平移或者缩放关系,我们在视觉上的感受是两者之间并无太大差异,图像信息可能被完整地保留了下来(比如大头照)。但是他们计算MSE的时候会有一个不太理想的结果。
PSNR
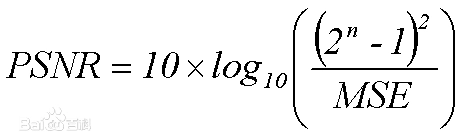
注意到MSE在分母上,意味着PSNR数值越高,则两图像相似度更高。
附matlab代码如下:
function [ output ] = PSNR( img1,img2)
%PSNR 峰值信噪比
if sum(sum(img1-img2)) == 0
error('Those pictures are the same');
end
MAX=1; %图像有多少灰度级(我这里定为1)
% 归一化
if (max(max(img1))-min(min(img1))) ~= 0
img1 = (img1-min(min(img1)))./(max(max(img1))-min(min(img1)));
end
if (max(max(img1))-min(min(img1))) ~= 0
img2 = (img2-min(min(img2)))./(max(max(img2))-min(min(img2)));
end
%
MSE=sum(sum((img1-img2).^2))/(1024*1024); %图片像素设为1024 x 1024
output=20*log10(MAX/sqrt(MSE)); %峰值信噪比
end
SNR
信噪比是信号均值与背景标准偏差的比值:
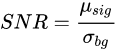
这个结构与PSNR一致。分子分母的量纲一致,相除后便于比较。
为什么是这个结构
引入一个变量
变异系数(Coefficient of Variation)
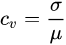
是信噪比的倒数。
是概率分布离散程度的一个归一化量度。
一般来说,变异值平均水平高,其离散程度的测度值越大,反之越小。
变异系数是衡量资料中各观测值变异程度的另一个统计量。当进行两个或多个资料变异程度的比较时,如果度量单位与平均数相同,可以直接利用标准差来比较。如果单位和(或)平均数不同时,比较其变异程度就不能采用标准差,而需采用标准差与平均数的比值(相对值)来比较。
变异系数可以消除单位和(或)平均数不同对两个或多个资料变异程度比较的影响。
也就是说,这个变量是个不带单位的指数。
举个例子:
已知某良种猪场长白成年母猪平均体重为190kg,标准差为10.5kg,而大约克成年母猪平均体重为196kg,标准差为8.5kg,试问两个品种的成年母猪,哪一个体重变异程度大。
此例观测值虽然都是体重,单位相同,但它们的平均数不相同,只能用变异系数来比较其变异程度的大小。
由于,长白成年母猪体重的变异系数为 5.53%
大约克成年母猪体重的变异系数为4.34%
所以,长白成年母猪体重的变异程度大于大约克成年母猪。
变异系数类比SNR
也就是说,我们讲像素值的离散程度等价于图片的噪声,离散程度越高,图像的噪声越大。
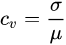
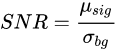
SNR越高,像素的离散程度越低,图像质量(可能)越好。
文章出处登录后可见!
