参考：

http://t.csdn.cn/8ApfD

‘http://t.csdn.cn/ZmEOJ

核心观点： 

• 前一层的通道数（特征图数量），决定这一层过滤器的深度；
• 这一层过滤器的数量，决定这一层输出的通道数（特征图数量）

神经网络每一层输出矩阵的形状一般是4个维度[y1, y2, y3, y4]

• y1 通常是batch_size,就是每一圈丢几张图片进去训练
• y2 y3 通常是图片的长宽
• y4 就是图片的通道数

目录

一 过滤器与卷积核的区别

二 通道数与特征图数

三 神经网络的输出矩阵形状变化

一 过滤器与卷积核的区别

        首先我们需要理解过滤器与卷积核的区别.

        卷积核是一个二维的概念 （2，2）就是一个2×2的卷积核。

        过滤器是一个三维的概念   3×2×2 ，就是3个2×2的卷积核集和成一个三维的过滤器，卷积核的数量就是过滤器的深度。

二 通道数与特征图数

        上面说到，过滤器是几个卷积核的集和，那么到底是几个卷积核呢？

        这一层过滤器的深度，由前一层的通道数（特征图数量决定）。

         通道数＝特征图数量，不要误认为前一层图像是3通道的然后这一层输出的特征图也是3通道的。

        比如，第一层输入为RGB3通道，则是3张特征图（每个通道的像素都组成一张特征图）。则第二层的过滤器的深度为3，每个卷积核与对应特征图卷积，得到一张新的特征图。卷积过程如下：

图片来源于：http://t.csdn.cn/8ApfD ，博主写的很好，大家可以去看看

        也就是1个过滤器由3个卷积核组成，输出1个新的特征图。

• 前一层的通道数（特征图数量），决定这一层过滤器的深度；
• 这一层过滤器的数量，决定这一层输出的通道数（特征图数量）

三 神经网络的输出矩阵形状变化

        以下面的7层卷积神经网络进行讲解，输入为mnist的手写数据集，图片为28×28的灰度图片。也就是形状为（28， 28， 1）

model = tf.keras.models.Sequential([
    tf.keras.layers.Conv2D(64, (3, 3), activation = 'relu',
                           input_shape=(28, 28, 1)), # 输出64张特征图
    tf.keras.layers.MaxPooling2D(2, 2),
    tf.keras.layers.Conv2D(64, (3, 3), activation='relu'), #卷积核为3维， 3×3×64，然后共有64个这样的三维卷积核
    tf.keras.layers.MaxPooling2D(2, 2), #在全连接网络上增加了这样四层
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dense(10, activation='softmax')
])

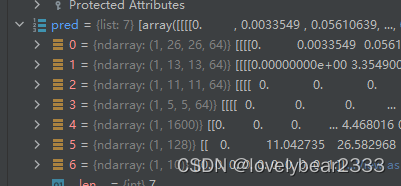
          第一层有64个3×3的过滤器，则输出形状变为了[1, 26, 26, 64]。前面的1是batch_size。26是由于卷积没有加padding，卷积之后少了两行两列。64是因为有64个过滤器，卷积出来之后有64个特征图也就是64个通道。

         第二层是经过 最大值池化，就是在每一个2×2的区域里，只保留值最大的一个像素值。所以输出变为了[1, 13, 13, 64]。

        第三层是64个3×3的过滤器，注意，这里的过滤器是三维的，深度为64。也就是64个64×3×3的过滤器，卷积之后的通道数为64。输出变为[1,11,11,64]

        其余读者自行推导。