论文链接:https://bmvc2022.mpi-inf.mpg.de/0239.pdf
代码链接:https://github.com/huiyu8794/LDCNet
1 FAS面临的挑战
(1)与其他cv任务不同,FAS处理的是真假人脸之间高度相似的特征,需要更加精细的特征表示来表征与人脸呈现攻击相关的内在特征;
(2)不同benchmark的数据集有不同的数据分布,在一个数据集上训练的模型,在另一个数据集上的测试结果往往不佳。
2 创新点
(1)提出了Learnable Descriptive Convolution (LDC)来自适应地学习FAS中精细的纹理特征;
(2)结合triplet mining和dual-attention supervision的策略来协同监督 LDCNet 以学习域不变和真假人脸判别特征。
3 方法论
3.1 LDC
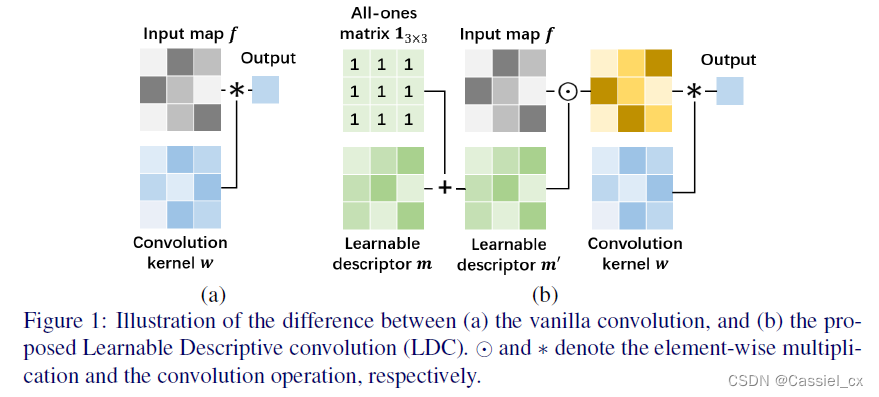
(1)标准卷积与中心差分卷积
标准卷积:
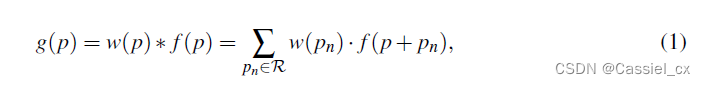
R为3×3的局部区域({(-1,-1),(-1,0),…,(0,1),(1,1)}),p为当前像素点。
中心差分卷积:
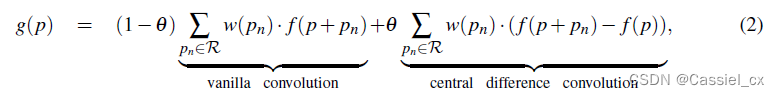
(2)LDC
虽然中心差分卷积等合并了不同的局部描述符来扩展标准卷积,但它们都采用了预定义好的局部描述符并且仍然保留了卷积核 w 中的学习能力,这些局部描述符不会在模型训练中进行更新。预定义的描述符无法灵活地捕获各种纹理特征。因此,作者提出了LDC,

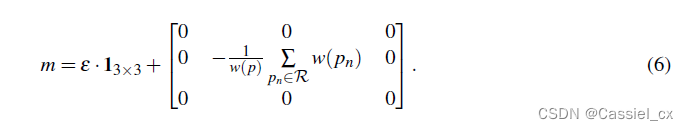
class conv3x3_learn(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size=3, stride=1,
padding=1, dilation=1, groups=1, bias=False):
# conv.weight.size() = [out_channels, in_channels, kernel_size, kernel_size]
super(conv3x3_learn, self).__init__()
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size, stride=stride, padding=padding,
dilation=dilation, groups=groups, bias=bias) # [12,3,3,3]
self.center_mask = torch.tensor([[0, 0, 0],
[0, 1, 0],
[0, 0, 0]]).cuda()
self.base_mask = nn.Parameter(torch.ones(self.conv.weight.size()), requires_grad=False) # [12,3,3,3]
self.learnable_mask = nn.Parameter(torch.ones([self.conv.weight.size(0), self.conv.weight.size(1)]),
requires_grad=True) # [12,3]
self.learnable_theta = nn.Parameter(torch.ones(1) * 0.5, requires_grad=True) # [1]
print(self.learnable_mask[:, :, None, None].shape)
def forward(self, x):
mask = self.base_mask - self.learnable_theta * self.learnable_mask[:, :, None, None] * \
self.center_mask * self.conv.weight.sum(2).sum(2)[:, :, None, None]
out_diff = F.conv2d(input=x, weight=self.conv.weight * mask, bias=self.conv.bias, stride=self.conv.stride,
padding=self.conv.padding,
groups=self.conv.groups)
return out_diff3.2 LDCNet
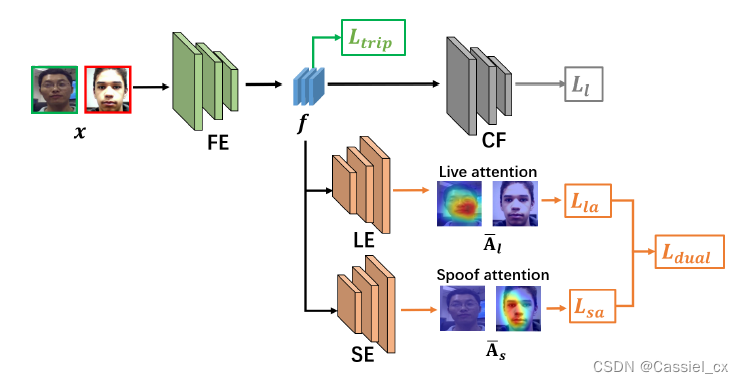
FE:feature extractor;CF:live/spoof classifier;LE:live attention estimator;SE:spoof attention estimator
其中,分类器由交叉熵损失函数优化:
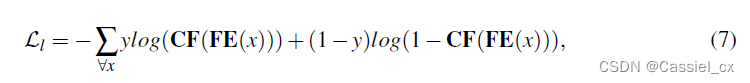
3.3 Triplet Mining
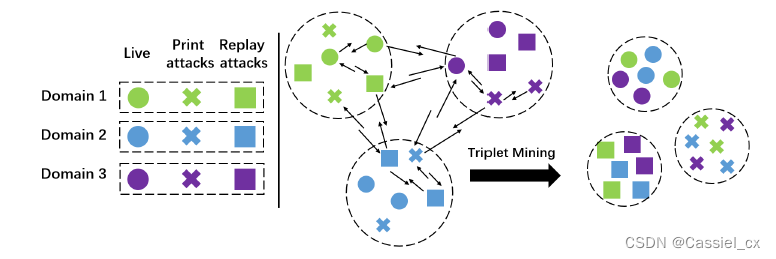
作者在LDCNet中采用triplet mining来约束FE,以学习域不变特征。如下图所示,假设不同源域均有3个类别的标签(live, print attack, and replay attack),triplet mining使intra-class pairs相互靠近,inter-class pairs相互远离,
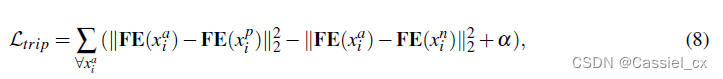
class HardTripletLoss(nn.Module):
"""Hard/Hardest Triplet Loss
(pytorch implementation of https://omoindrot.github.io/triplet-loss)
For each anchor, we get the hardest positive and hardest negative to form a triplet.
"""
def __init__(self, margin=0.1, hardest=True, squared=False):
"""
Args:
margin: margin for triplet loss
hardest: If true, loss is considered only hardest triplets.
squared: If true, output is the pairwise squared euclidean distance matrix.
If false, output is the pairwise euclidean distance matrix.
"""
super(HardTripletLoss, self).__init__()
self.margin = margin
self.hardest = hardest
self.squared = squared
def forward(self, embeddings, labels, device_id='cuda:0'):
"""
Args:
labels: labels of the batch, of size (batch_size,)
embeddings: tensor of shape (batch_size, embed_dim)
Returns:
triplet_loss: scalar tensor containing the triplet loss
"""
pairwise_dist = _pairwise_distance(embeddings, squared=self.squared) # [bs, bs]
#print("pairwise_dist:",pairwise_dist)
if self.hardest:
# Get the hardest positive pairs
mask_anchor_positive = _get_anchor_positive_triplet_mask(labels, device_id).float()
valid_positive_dist = pairwise_dist * mask_anchor_positive
hardest_positive_dist, _ = torch.max(valid_positive_dist, dim=1, keepdim=True)
# Get the hardest negative pairs
mask_anchor_negative = _get_anchor_negative_triplet_mask(labels).float()
max_anchor_negative_dist, _ = torch.max(pairwise_dist, dim=1, keepdim=True)
anchor_negative_dist = pairwise_dist + max_anchor_negative_dist * (
1.0 - mask_anchor_negative)
hardest_negative_dist, _ = torch.min(anchor_negative_dist, dim=1, keepdim=True)
# Combine biggest d(a, p) and smallest d(a, n) into final triplet loss
triplet_loss = F.relu(hardest_positive_dist - hardest_negative_dist + self.margin)
triplet_loss = torch.mean(triplet_loss)
else:
anc_pos_dist = pairwise_dist.unsqueeze(dim=2)
#print("anc_pos_dist shape",anc_pos_dist.shape)
anc_neg_dist = pairwise_dist.unsqueeze(dim=1)
#print("anc_neg_dist shape", anc_neg_dist.shape)
# Compute a 3D tensor of size (batch_size, batch_size, batch_size)
# triplet_loss[i, j, k] will contain the triplet loss of anc=i, pos=j, neg=k
# Uses broadcasting where the 1st argument has shape (batch_size, batch_size, 1)
# and the 2nd (batch_size, 1, batch_size)
loss = anc_pos_dist - anc_neg_dist + self.margin
#print("loss shape",loss.shape)
mask = _get_triplet_mask(labels).float()
triplet_loss = loss * mask
# Remove negative losses (i.e. the easy triplets)
triplet_loss = F.relu(triplet_loss)
# Count number of hard triplets (where triplet_loss > 0)
hard_triplets = torch.gt(triplet_loss, 1e-16).float()
num_hard_triplets = torch.sum(hard_triplets)
triplet_loss = torch.sum(triplet_loss) / (num_hard_triplets + 1e-16)
return triplet_loss
def _pairwise_distance(x, squared=False, eps=1e-16):
# Compute the 2D matrix of distances between all the embeddings.
# got the dot product between all embeddings
#print("x shape",x.shape)
cor_mat = torch.matmul(x, x.t())
#print("cor_mat shape:", cor_mat.shape)
# Get squared L2 norm for each embedding. We can just take the diagonal of `dot_product`.
# This also provides more numerical stability (the diagonal of the result will be exactly 0).
norm_mat = cor_mat.diag() # 输出矩阵主对角线上的元素
#print("norm_mat shape:", norm_mat)
# Compute the pairwise distance matrix as we have:
# ||a - b||^2 = ||a||^2 - 2 <a, b> + ||b||^2
# shape (batch_size, batch_size)
#print("norm_mat.unsqueeze(0) shape:", norm_mat.unsqueeze(0).shape)
distances = norm_mat.unsqueeze(1) - 2 * cor_mat + norm_mat.unsqueeze(0)
# Because of computation errors, some distances might be negative so we put everything >= 0.0
distances = F.relu(distances)
if not squared:
# Because the gradient of sqrt is infinite when distances == 0.0 (ex: on the diagonal)
# we need to add a small epsilon where distances == 0.0
mask = torch.eq(distances, 0.0).float()
distances = distances + mask * eps
distances = torch.sqrt(distances)
# Correct the epsilon added: set the distances on the mask to be exactly 0.0
distances = distances * (1.0 - mask)
return distances
def _get_anchor_positive_triplet_mask(labels, device_id):
# Return a 2D mask where mask[a, p] is True iff a and p are distinct and have same label.
device = torch.device(device_id if torch.cuda.is_available() else "cpu")
indices_not_equal = torch.eye(labels.shape[0]).to(device).byte() ^ 1 # 对角矩阵取反
# Check if labels[i] == labels[j]
labels_equal = torch.unsqueeze(labels, 0) == torch.unsqueeze(labels, 1)
mask = indices_not_equal * labels_equal
return mask
def _get_anchor_negative_triplet_mask(labels):
# Return a 2D mask where mask[a, n] is True iff a and n have distinct labels.
# Check if labels[i] != labels[k]
labels_equal = torch.unsqueeze(labels, 0) == torch.unsqueeze(labels, 1)
mask = labels_equal ^ 1
return mask
def _get_triplet_mask(labels):
"""Return a 3D mask where mask[a, p, n] is True iff the triplet (a, p, n) is valid.
A triplet (i, j, k) is valid if:
- i, j, k are distinct
- labels[i] == labels[j] and labels[i] != labels[k]
"""
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# Check that i, j and k are distinct
indices_not_same = torch.eye(labels.shape[0]).to(device).byte() ^ 1
i_not_equal_j = torch.unsqueeze(indices_not_same, 2)
i_not_equal_k = torch.unsqueeze(indices_not_same, 1)
j_not_equal_k = torch.unsqueeze(indices_not_same, 0)
distinct_indices = i_not_equal_j * i_not_equal_k * j_not_equal_k
# Check if labels[i] == labels[j] and labels[i] != labels[k]
label_equal = torch.eq(torch.unsqueeze(labels, 0), torch.unsqueeze(labels, 1))
i_equal_j = torch.unsqueeze(label_equal, 2)
i_equal_k = torch.unsqueeze(label_equal, 1)
valid_labels = i_equal_j * (i_equal_k ^ 1)
mask = distinct_indices * valid_labels # Combine the two masks
return mask3.4 Dual Attention Supervision
由于二分类标签无法满足FAS的需求,作者提出了dual-attention supervision,包含live attention和spoof attention,为LDCNet提供具有细粒度信息的监督。作者使用Class Activation Map为LE和SE生成quasi-ground truth。具体来说,先预训练FE和CF,以获得live activation map 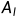 和spoof activation map
和spoof activation map 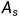 ,
,
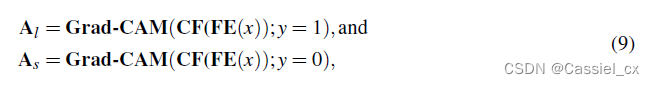

使用MSE约束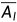 和
和 ,
,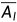 和
和 均为1×32×32的tensor,
均为1×32×32的tensor,
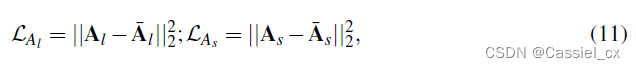
其中,假体图片的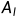 和真人图片的
和真人图片的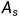 为0
为0
3.5 Total Loss and Live/Spoof Classification
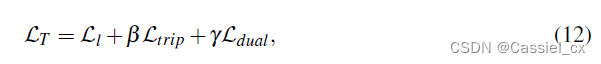
其中,β=0.1,γ=0.004
在推理阶段,检测分数为:

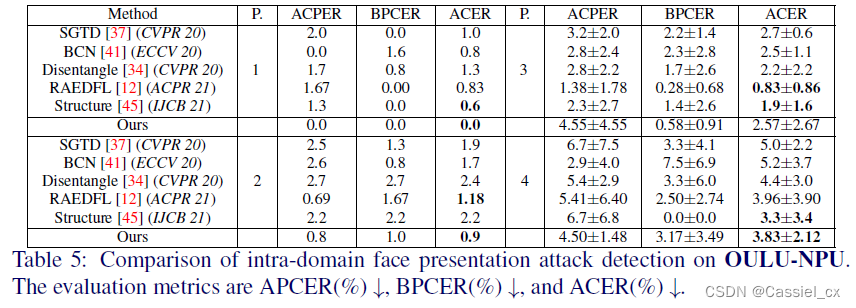
4 实验结果
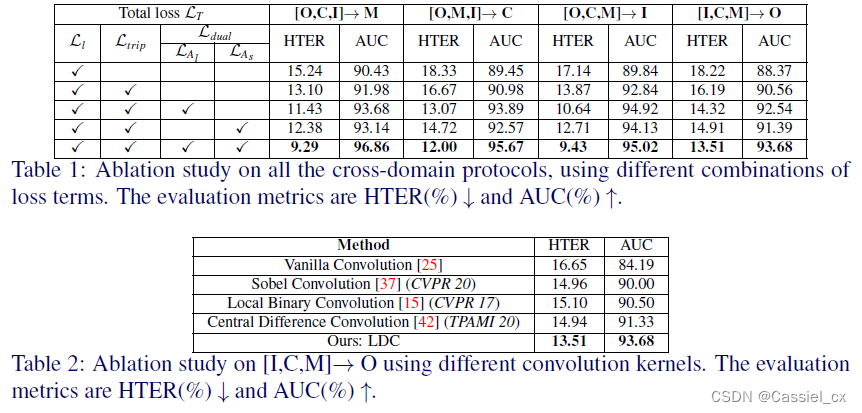
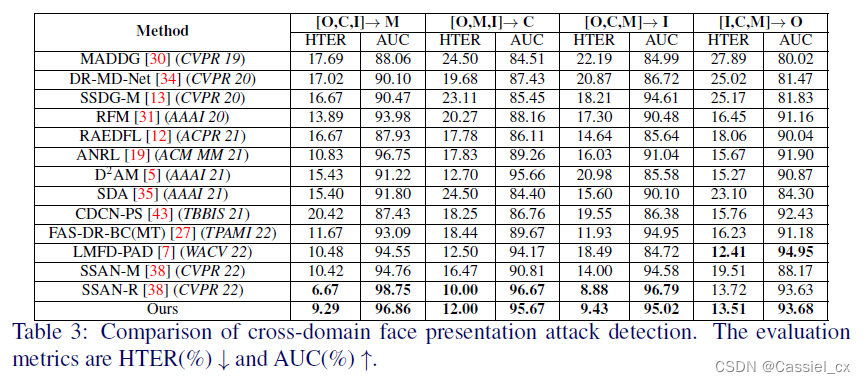
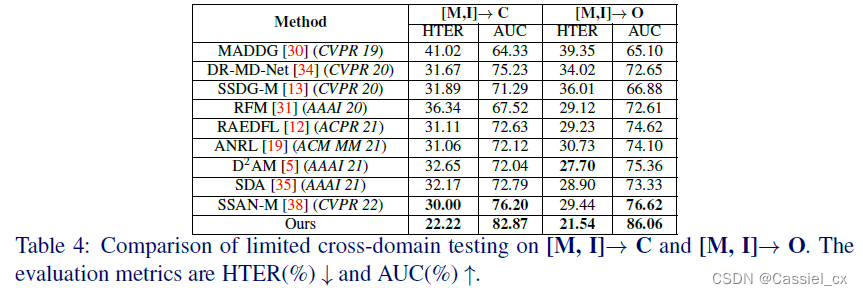

文章出处登录后可见!
