论文地址:Wise-IoU: Bounding Box Regression Loss with Dynamic Focusing Mechanism
GitHub:https://github.com/Instinct323/wiou
摘要:目标检测作为计算机视觉的核心问题,其检测性能依赖于损失函数的设计。边界框损失函数作为目标检测损失函数的重要组成部分,其良好的定义将为目标检测模型带来显著的性能提升。近年来的研究大多假设训练数据中的示例有较高的质量,致力于强化边界框损失的拟合能力。但我们注意到目标检测训练集中含有低质量示例,如果一味地强化边界框对低质量示例的回归,显然会危害模型检测性能的提升。Focal-EIoU v1 被提出以解决这个问题,但由于其聚焦机制是静态的,并未充分挖掘非单调聚焦机制的潜能。基于这个观点,我们提出了动态非单调的聚焦机制,设计了 Wise-IoU (WIoU)。动态非单调聚焦机制使用“离群度”替代 IoU 对锚框进行质量评估,并提供了明智的梯度增益分配策略。该策略在降低高质量锚框的竞争力的同时,也减小了低质量示例产生的有害梯度。这使得 WIoU 可以聚焦于普通质量的锚框,并提高检测器的整体性能。将WIoU应用于最先进的单级检测器 YOLOv7 时,在 MS-COCO 数据集上的 AP-75 从 53.03% 提升到 54.50%
前言:因为我能使用的算力有限,所以做实验时只在 YOLOv7 上做了。而且因为完整的 MS-COCO 需要更大的参数量,训练一个模型需要 3 天时间,所以我只取了其中四分之一的数据进行训练 (28474 张训练图片)。虽然实验量相比其它工作是远远不足的,但这几天中文社区的反应让我感觉这篇文章还有救哈哈哈。为了支持广大计算机视觉研究者的工作,我决定来这里讲解一下理论部分和代码实战
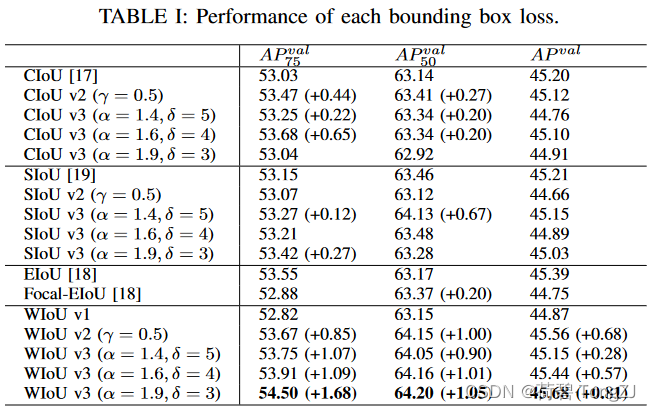
CIoU、SIoU 的 v2 使用和 WIoU v2 一致的单调聚焦机制,v3 使用和 WIoU v3 一致的动态非单调聚焦机制,详见论文的消融实验
在计算速度上,WIoU 所增加的计算成本主要在于聚焦系数的计算、IoU 损失的均值统计。在实验条件相同时,WIoU 因为没有对纵横比进行计算反而有更快的速度,WIoU 的计算耗时为 CIoU 的 87.2%
在性能提升上,数据集的标注质量越差 (当然差到一定程度就不叫数据集了),WIoU 相对其它边界框损失的表现越好。比如说我在一个检测火焰的比赛里用的 WIoU (那时的初版还比较捞) 使 mAP 提升了 1.70% (相比 CIoU)
这篇博客没有像论文那么详细,大家有什么地方看不明白的欢迎在评论区提问,我会抽时间补上的 ~
现有工作
记锚框为 ,目标框为
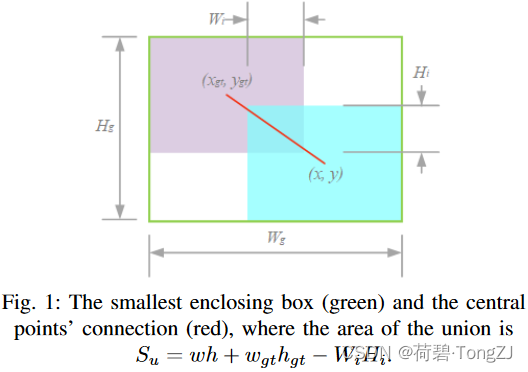
IoU 用于度量目标检测任务中预测框与真实框的重叠程度,定义为:
同时,IoU 有一个致命的缺陷,可以在下面公式中观察到。当边界框之间没有重叠时 ,
现有的工作考虑了许多与包围盒相关的几何因素并构造了惩罚项 来解决这个问题,现有的边界框损失都是基于加法的损失,并遵循以下范式:
Distance-IoU
DIoU 将惩罚项定义为中心点连接的归一化长度:
同时为最小包围框的尺寸 提供了负梯度,这将使得
增大而阻碍预测框与目标框重叠:
但不可否认的是,距离度量的确是一个极其有效的解决方案,成为高效边界框损失的必要因子。EIoU 在此基础上加大了对距离度量的惩罚力度,其惩罚项定义为:
Complete-IoU
在 的基础上,CIoU 增加了对纵横比一致性的考虑:
其中的 描述了纵横比一致性:
其中 反向传播的梯度满足
,也就是
不可能为预测框的宽高提供同号的梯度。在前文对 DIoU 的分析中可知 DIoU 会产生负梯度
,当这个负梯度与
正好抵消时,会导致预测框无法优化。而 CIoU 对纵横比一致性的考虑将打破这种僵局
Scylla-IoU
Zhora Gevorgyan 证明了中心对齐的边界框会具有更快的收敛速度,以 angle cost、distance cost、shape cost 构造了 SIoU。其中 angle cost 描述了边界框中心连线与 x-y 轴的最小夹角:
distance cost 描述了两边界框的中心点在x轴和y轴上的归一化距离,其惩罚力度与 angle cost 正相关。distance cost 被定义为:
shape cost 描述了两边界框的形状差异,当两边界框的尺寸不一致时不为 0。shape cost 被定义为:
与
类似,它们都由 distance cost 和 shape cost 组成:
本文方法
本文所涉及的聚焦机制有以下几种:
- 静态:当边界框的 IoU 为某一指定值时有最高的梯度增益,如 Focal EIoU v1
- 动态:享有最高梯度增益的边界框的条件处于动态变化中,如 WIoU v3
- 单调:梯度增益随损失值的增加而单调增加,如 Focal loss
- 非单调:梯度增益随损失值的增加呈非单调变化
WIoU v1 构造了基于注意力的边界框损失,WIoU v2 和 v3 则是在此基础上通过构造梯度增益 (聚焦系数) 的计算方法来附加聚焦机制
Wise-IoU v1
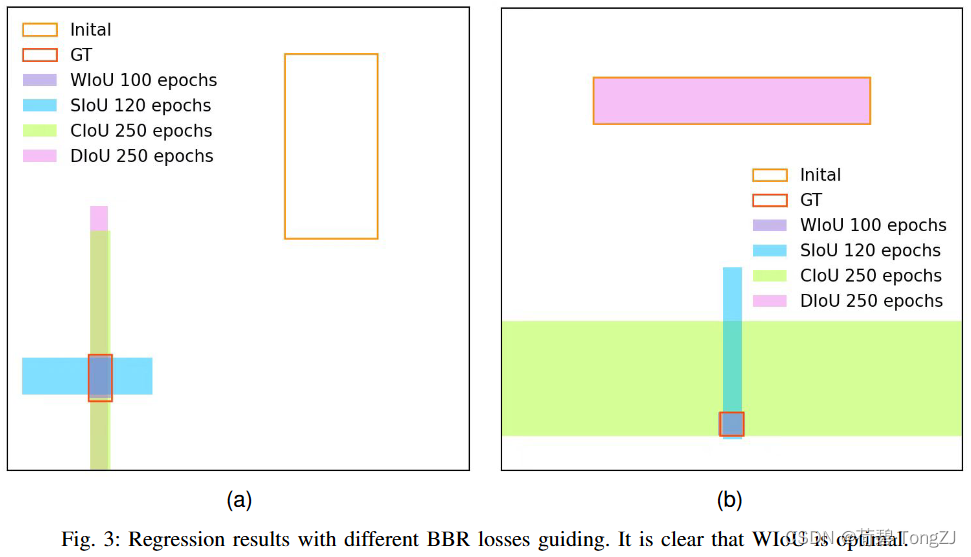
因为训练数据中难以避免地包含低质量示例,所以如距离、纵横比之类的几何度量都会加剧对低质量示例的惩罚从而使模型的泛化性能下降。好的损失函数应该在锚框与目标框较好地重合时削弱几何度量的惩罚,不过多地干预训练将使模型有更好的泛化能力。在此基础上,我们根据距离度量构建了距离注意力,得到了具有两层注意力机制的 WIoU v1:
,这将显著放大普通质量锚框的
,这将显著降低高质量锚框的
,并在锚框与目标框重合较好的情况下显著降低其对中心点距离的关注
为了防止 产生阻碍收敛的梯度,将
从计算图 (上标 * 表示此操作) 中分离。因为它有效地消除了阻碍收敛的因素,所以我们没有引入新的度量指标,如纵横比
Wise-IoU v2
Focal Loss 设计了一种针对交叉熵的单调聚焦机制,有效降低了简单示例对损失值的贡献。这使得模型能够聚焦于困难示例,获得分类性能的提升。类似地,我们构造了 的单调聚焦系数
:
在模型训练过程中,梯度增益 随着
的减小而减小,导致训练后期收敛速度较慢。因此,引入
的均值作为归一化因子:
其中的 为动量为
的滑动平均值,动态更新归一化因子使梯度增益
整体保持在较高水平,解决了训练后期收敛速度慢的问题
Wise-IoU v3
定义离群度以描述锚框的质量,其定义为:
离群度小意味着锚框质量高,我们为其分配一个小的梯度增益,以便使边界框回归聚焦到普通质量的锚框上。对离群度较大的锚框分配较小的梯度增益,将有效防止低质量示例产生较大的有害梯度。我们利用 构造了一个非单调聚焦系数并将其应用于 WIoU v1:
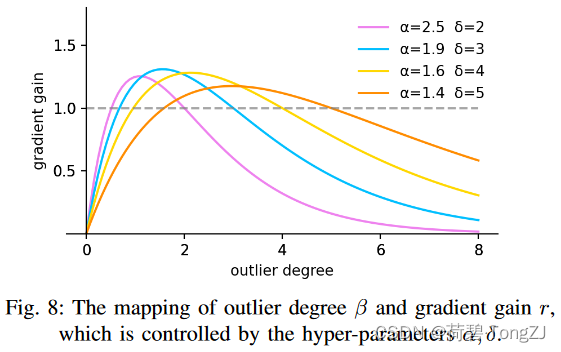
其中,当 时,
使得
。当锚框的离群程度满足
(
为定值)时,锚框将获得最高的梯度增益。由于
是动态的,锚框的质量划分标准也是动态的,这使得 WIoU v3 在每一时刻都能做出最符合当前情况的梯度增益分配策略
为了防止低质量锚框在训练初期落后,我们初始化 使得
的锚框具有最高的梯度增益。为了在训练的早期阶段保持这样的策略,需要设置一个小的动量
来延迟
接近真实值
的时间。对于 batchs 数量为
的训练,我们建议将动量设置为:
这种设置使得经过 轮训练后有
。在训练的中后期,WIoU v3 将小梯度增益分配给低质量的锚框以减少有害梯度。同时 WIoU v3 会聚焦于普通质量的锚框,提高模型的定位性能
核心代码
下面这个类可以计算现有的边界框损失 (IoU,GIoU,DIoU,CIoU,EIoU,SIoU,WIoU),核心的类变量有:
- iou_mean:即
的滑动平均值,每次程序刚开始运行时初始化为 1。如果训练中断导致该值重置,需要将该值恢复为中断前的值,否则会导致性能增速下降
- monotonus:其指示了边界框损失使用单调聚焦机制 (e.g., WIoU v2) 或是非单调聚焦机制 (e.g., WIoU v3),具体看该类的文档
- momentum:遵循
的设置。当
足够小时,验证集的 IoU 基本不影响
的值,此时不需要使用 eval 和 train 函数指定训练模式;否则需要使用 eval 和 train 函数指定训练模式
此外,聚焦机制会对边界框损失的值进行缩放,具体通过实例方法 _scaled_loss 实现
import math
import torch
class IoU_Cal:
''' pred, target: x0,y0,x1,y1
monotonous: {
None: origin
True: monotonic FM
False: non-monotonic FM
}
momentum: The momentum of running mean'''
iou_mean = 1.
monotonous = False
momentum = 1 - pow(0.5, exp=1 / 7000)
_is_train = True
def __init__(self, pred, target):
self.pred, self.target = pred, target
self._fget = {
# x,y,w,h
'pred_xy': lambda: (self.pred[..., :2] + self.pred[..., 2: 4]) / 2,
'pred_wh': lambda: self.pred[..., 2: 4] - self.pred[..., :2],
'target_xy': lambda: (self.target[..., :2] + self.target[..., 2: 4]) / 2,
'target_wh': lambda: self.target[..., 2: 4] - self.target[..., :2],
# x0,y0,x1,y1
'min_coord': lambda: torch.minimum(self.pred[..., :4], self.target[..., :4]),
'max_coord': lambda: torch.maximum(self.pred[..., :4], self.target[..., :4]),
# The overlapping region
'wh_inter': lambda: self.min_coord[..., 2: 4] - self.max_coord[..., :2],
's_inter': lambda: torch.prod(torch.relu(self.wh_inter), dim=-1),
# The area covered
's_union': lambda: torch.prod(self.pred_wh, dim=-1) +
torch.prod(self.target_wh, dim=-1) - self.s_inter,
# The smallest enclosing box
'wh_box': lambda: self.max_coord[..., 2: 4] - self.min_coord[..., :2],
's_box': lambda: torch.prod(self.wh_box, dim=-1),
'l2_box': lambda: torch.square(self.wh_box).sum(dim=-1),
# The central points' connection of the bounding boxes
'd_center': lambda: self.pred_xy - self.target_xy,
'l2_center': lambda: torch.square(self.d_center).sum(dim=-1),
# IoU
'iou': lambda: 1 - self.s_inter / self.s_union
}
self._update(self)
def __setitem__(self, key, value):
self._fget[key] = value
def __getattr__(self, item):
if callable(self._fget[item]):
self._fget[item] = self._fget[item]()
return self._fget[item]
@classmethod
def train(cls):
cls._is_train = True
@classmethod
def eval(cls):
cls._is_train = False
@classmethod
def _update(cls, self):
if cls._is_train: cls.iou_mean = (1 - cls.momentum) * cls.iou_mean + \
cls.momentum * self.iou.detach().mean().item()
def _scaled_loss(self, loss, alpha=1.9, delta=3):
if isinstance(self.monotonous, bool):
beta = self.iou.detach() / self.iou_mean
if self.monotonous:
loss *= beta.sqrt()
else:
divisor = delta * torch.pow(alpha, beta - delta)
loss *= beta / divisor
return loss
@classmethod
def IoU(cls, pred, target, self=None):
self = self if self else cls(pred, target)
return self.iou
@classmethod
def WIoU(cls, pred, target, self=None):
self = self if self else cls(pred, target)
dist = torch.exp(self.l2_center / self.l2_box.detach())
return self._scaled_loss(dist * self.iou)
@classmethod
def EIoU(cls, pred, target, self=None):
self = self if self else cls(pred, target)
penalty = self.l2_center / self.l2_box.detach() \
+ torch.square(self.d_center / self.wh_box.detach()).sum(dim=-1)
return self._scaled_loss(self.iou + penalty)
@classmethod
def GIoU(cls, pred, target, self=None):
self = self if self else cls(pred, target)
return self._scaled_loss(self.iou + (self.s_box - self.s_union) / self.s_box)
@classmethod
def DIoU(cls, pred, target, self=None):
self = self if self else cls(pred, target)
return self._scaled_loss(self.iou + self.l2_center / self.l2_box)
@classmethod
def CIoU(cls, pred, target, eps=1e-4, self=None):
self = self if self else cls(pred, target)
v = 4 / math.pi ** 2 * \
(torch.atan(self.pred_wh[..., 0] / (self.pred_wh[..., 1] + eps)) -
torch.atan(self.target_wh[..., 0] / (self.target_wh[..., 1] + eps))) ** 2
alpha = v / (self.iou + v)
return self._scaled_loss(self.iou + self.l2_center / self.l2_box + alpha.detach() * v)
@classmethod
def SIoU(cls, pred, target, theta=4, self=None):
self = self if self else cls(pred, target)
# Angle Cost
angle = torch.arcsin(torch.abs(self.d_center).min(dim=-1)[0] / (self.l2_center.sqrt() + 1e-4))
angle = torch.sin(2 * angle) - 2
# Dist Cost
dist = angle[..., None] * torch.square(self.d_center / self.wh_box)
dist = 2 - torch.exp(dist[..., 0]) - torch.exp(dist[..., 1])
# Shape Cost
d_shape = torch.abs(self.pred_wh - self.target_wh)
big_shape = torch.maximum(self.pred_wh, self.target_wh)
w_shape = 1 - torch.exp(- d_shape[..., 0] / big_shape[..., 0])
h_shape = 1 - torch.exp(- d_shape[..., 1] / big_shape[..., 1])
shape = w_shape ** theta + h_shape ** theta
return self._scaled_loss(self.iou + (dist + shape) / 2)
在将 WIoU v3 引进 YOLOv7 时,先在 train_aux.py 中找到损失函数的位置。ComputeLossAuxOTA 是 train 的时候用的,找到其源代码并进行修改
因为 YOLOv7 对模型性能的比较主要利用 utils/metrics 里的 fitness 函数,与损失值无关。而 ComputeLoss 是在 eval 的时候用的,保证不出 bug 就行
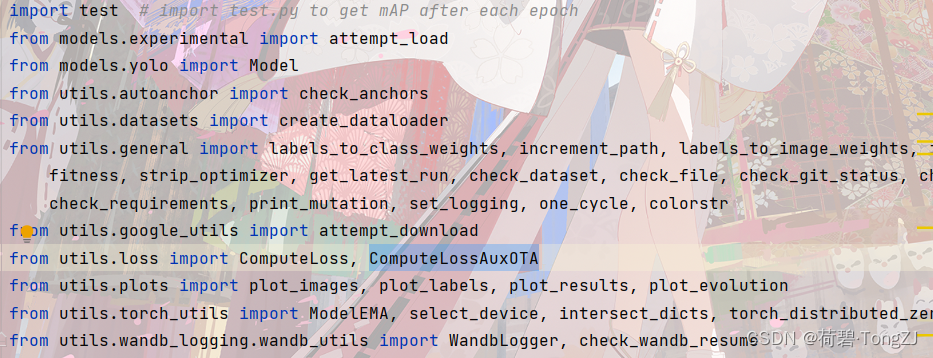
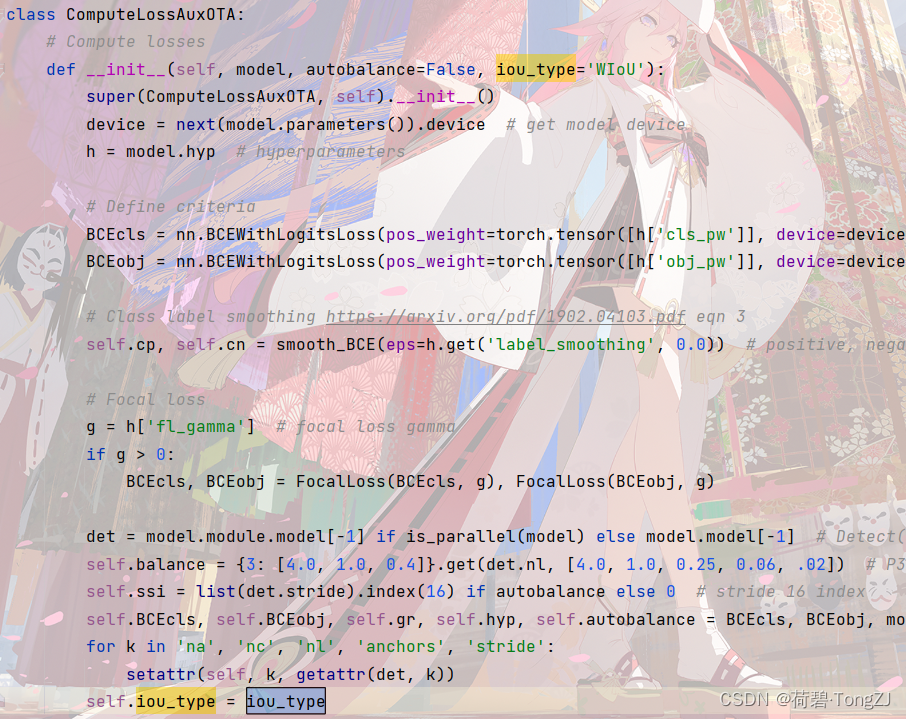
在初始化函数动一下手脚,指定使用的损失函数
再修改 __call__ 函数 (修改的行已用书签标注出)
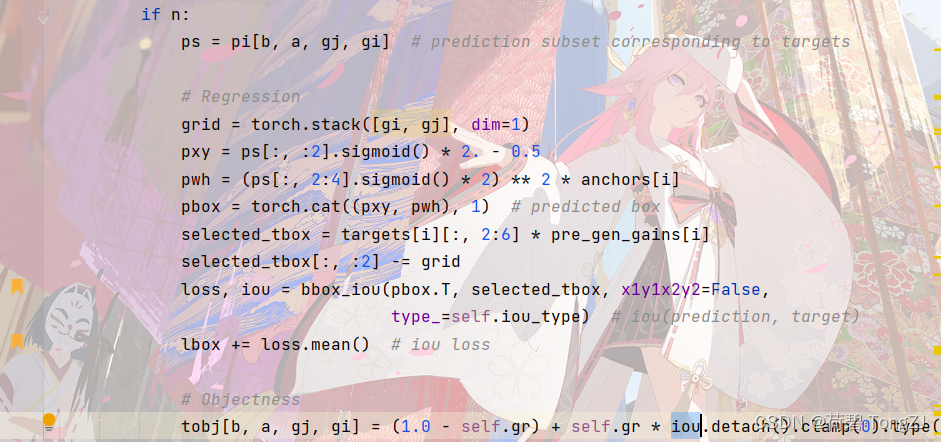
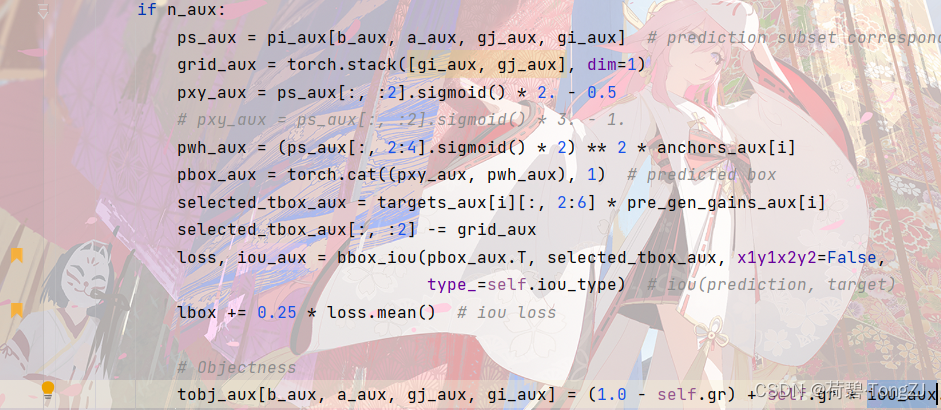
再找到 bbox_iou 函数的所在位置,修改边界框损失的计算方法
这里因为形参、返回值都和原函数不同,所以要检查 ComputeLoss 中调用这个函数的地方,以防报错
def bbox_iou(box1, box2, type_, x1y1x2y2=True):
# Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
box2 = box2.T
# Get the coordinates of bounding boxes
if x1y1x2y2: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
else: # transform from xywh to xyxy
b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2
# 将边界框信息拼接
b1 = torch.stack([b1_x1, b1_y1, b1_x2, b1_y2], dim=-1)
b2 = torch.stack([b2_x1, b2_y1, b2_x2, b2_y2], dim=-1)
self = IoU_Cal(b1, b2)
loss = getattr(IoU_Cal, type_)(b1, b2, self=self)
iou = 1 - self.iou
return loss, iou文章出处登录后可见!
