1 引言
在上一节中我们介绍了使用matplotlib进行数据可视化的几种表现方法,包括折线图、散点图、饼状图以及柱状图等, 今天我们来继续学习matplotlib的高级用法,主要包括网络图,流(stream)动图以及圆弧图,那么我们开始吧。。。
2 网络图
分散式网络: 中心化网络和分布(Distribution)式网络的混合(Mixing)体,在这种类(Cluster)型的网络中,少量节点的攻击会降低或破坏整个网络系统的性能.
分布(Distribution)式网络: 分布(Distribution)式网络具有抵御攻击的能力,即使在攻击后部分节点无法对网络作出贡献后,该网络仍将继续运行。这与中心化网络不同,中心化网络在中心节点受到攻击时可能会立刻破坏整个网络性能。
可视化结果:
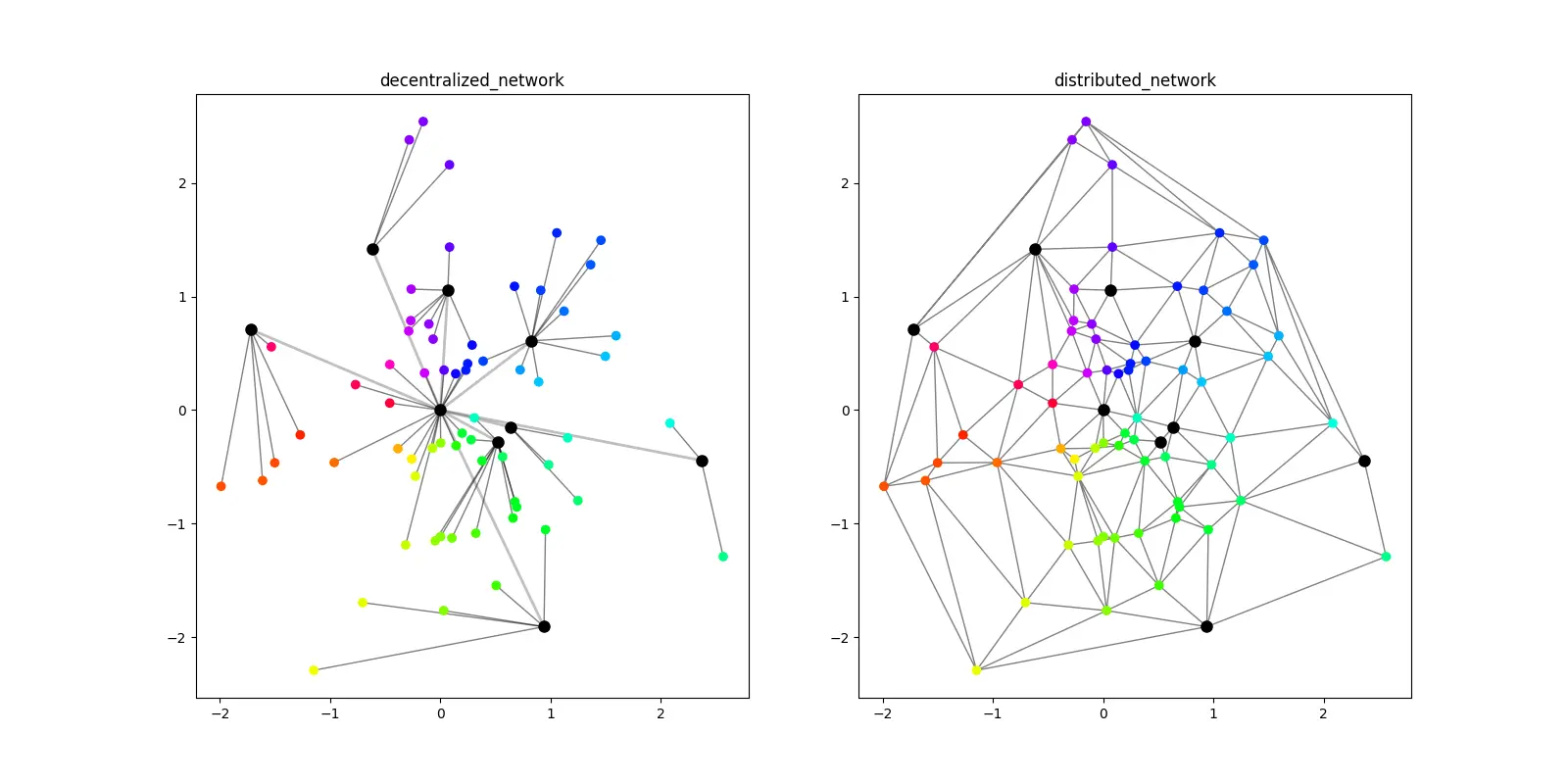
- 分散式网络:左上分散式网络图显示。
- 分布(Distribution)式网络:右上分布(Distribution)式网络图显示,通过三角剖分方法开发分布(Distribution)式网络显示。主要使用triplot()函数,绘制非结构化的三角形网格。
代码如下:
def test1():
# data
pn, cn = 64, 8
px = np.random.normal(0, 1, pn)
py = np.random.normal(0, 1, pn)
cx = np.random.normal(0, 1, cn)
cx = np.insert(cx, 0, 0)
cy = np.random.normal(0, 1, cn)
cy = np.insert(cy, 0, 0)
angle = (np.arctan2(py, px) + np.pi) / (2 * np.pi)
# param
distrib = tri.Triangulation(np.concatenate([px, cx]),
np.concatenate([py, cy]))
cmapRede = cm.get_cmap('hsv')
fig, (axA, axB) = plt.subplots(1, 2)
# left: draw each pt to the nearest center pt
for s, t in zip(px, py):
dist = ((s - cx) ** 2 + (t - cy) ** 2) ** 0.5
csel = dist <= dist.min()
for u, v in zip(cx[csel], cy[csel]):
axA.plot([s, u], [t, v], color='black', alpha=0.5,
linewidth=1, zorder=1)
# left: draw each center to (0,0)
for u, v in zip(cx, cy):
if u or v:
axA.plot([u, 0], [v, 0], color='black', alpha=0.25,
linewidth=2, zorder=1)
axA.scatter(px, py, c=cmapRede(angle), zorder=2)
axA.scatter(cx, cy, color='black', s=64, zorder=2)
axA.set_title('decentralized_network')
# right
axB.triplot(distrib, color='black', alpha=0.5, linewidth=1, zorder=1)
axB.scatter(px, py, c=cmapRede(angle), zorder=2)
axB.scatter(cx, cy, color='black', s=64, zorder=2)
axB.set_title('distributed_network')
plt.show()
triplot(*args, **kwargs)
参数:此方法接受以下描述的参数:
- x, y:这些参数是要绘制的数据的x和y坐标。
- triangulation:此参数是matplotlib.tri.Triangulation对象。
- **kwargs:此参数是文本属性,用于控制标签的外观。
3 流(stream)动图
给定路径,使用matplotlib中的Path模块,按照对应的路径上的控制点绘制相应的三次贝塞尔曲线图.
可视化结果:
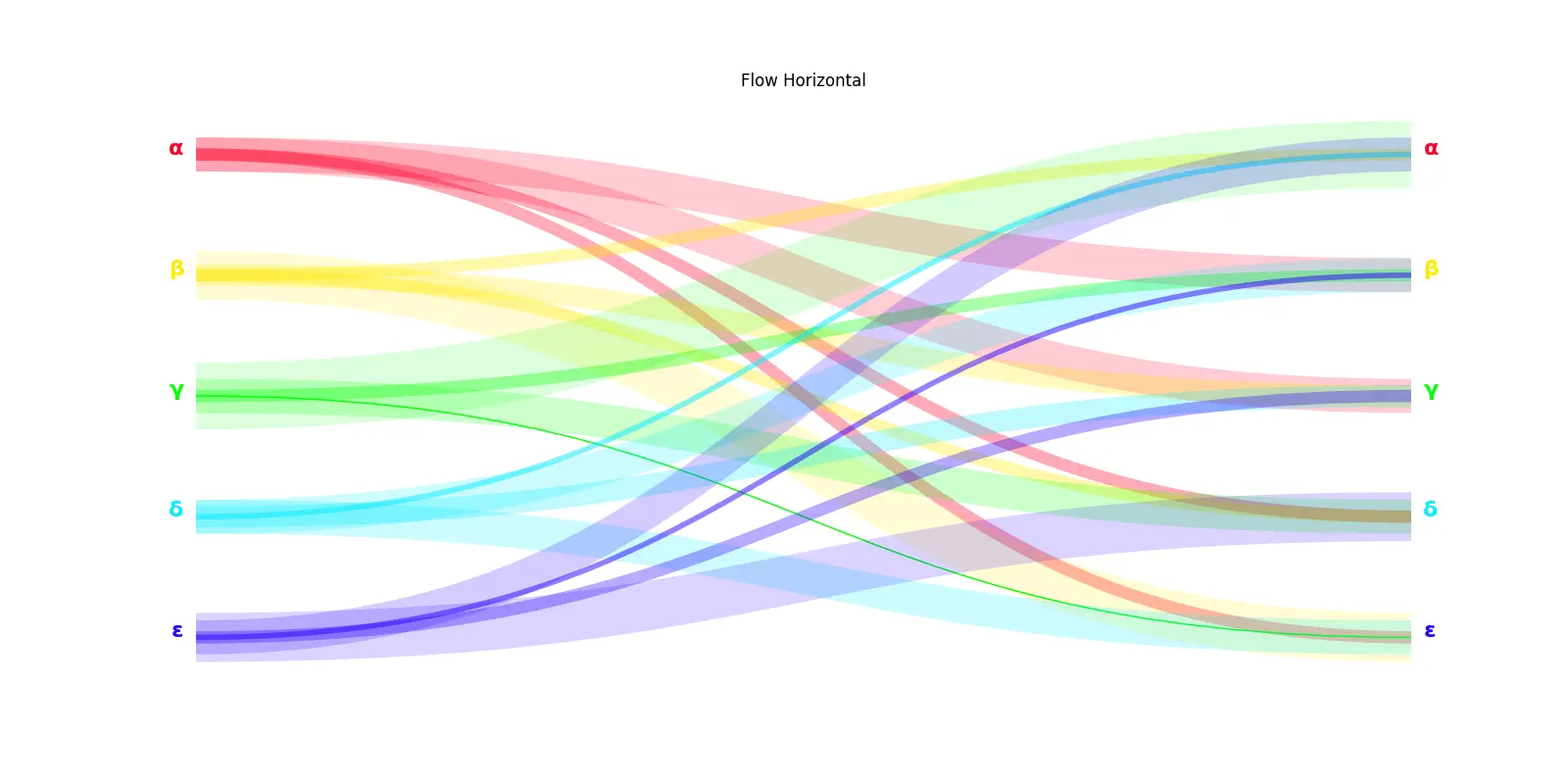
- 上图水平流(stream)向图可视化效果
代码如下:
def test2():
# dataflow
colecao = np.array(list('αβγδε'))
n = len(colecao)
indices = np.arange(n)
sel = lambda x: np.random.choice(x, 16)
mapa = np.array([sel(np.delete(indices, i)) for i in indices])
rede = colecao[mapa]
# param
from matplotlib.path import Path
import matplotlib.patches as patches
pontos = [Path.MOVETO, Path.CURVE4, Path.CURVE4, Path.CURVE4]
paleta = cm.get_cmap('gist_rainbow')
fig, axA = plt.subplots(1, 1)
# Flow horizontal
getPy = lambda x: (1 - x / n) - 0.1
for i, e in enumerate(colecao):
conx, cont = np.unique(rede[i], return_counts=True)
yo = getPy(i)
*cor, _ = paleta(i / n)
axA.text(-0.01, yo, e, ha='right', color=cor,
fontsize=16, fontweight='bold')
axA.text(1.01, yo, e, ha='left', color=cor,
fontsize=16, fontweight='bold')
for cx, ct in zip(conx, cont):
yi = getPy(np.where(colecao == cx)[0])
verts = [(0.0, yo), (0.5, yo), (0.5, yi), (1, yi)]
path = Path(verts, pontos)
patch = patches.PathPatch(path, facecolor='none', edgecolor=cor,
lw=ct ** 2, alpha=1 / ct)
axA.add_patch(patch)
axA.set_title('Flow Horizontal')
axA.axis('off')
plt.show()
PathPatch(path, **kwargs)
- path: 路径是 matplotlib.path.Path Object 。
- facecolor: 背景颜色
- edgecolor: 边缘颜色
- lw: linewidth 指定线的粗细
- alpha: 指定线的透明度
Path(vertices, codes=None)
- vertices: 是指的是路径path所经过的关键点的一系列坐标(x,y)
- codes指的是点与点之间到底是怎么连接的,取值如下:
– MOVETO : 拿起钢笔, 移动到给定的顶点。一般指的是 “起始点”
– LINETO : 从当前位置绘制直线到给定顶点。
– CURVE3 : 从当前位置 (用给定控制点) 绘制一个二次贝塞尔曲线到给定端点。
– CURVE4 : 从当前位置 (与给定控制点) 绘制三次贝塞尔曲线到给定端点。
– CLOSEPOLY : 将线段绘制到当前折线的起始点。
– STOP : 整个路径末尾的标记(token) (当前不需要和忽略)
4 圆弧图
给定圆弧路径,使用matplotlib中的Path模块,按照对应的路径绘制相应的圆弧路径图.
可视化结果:
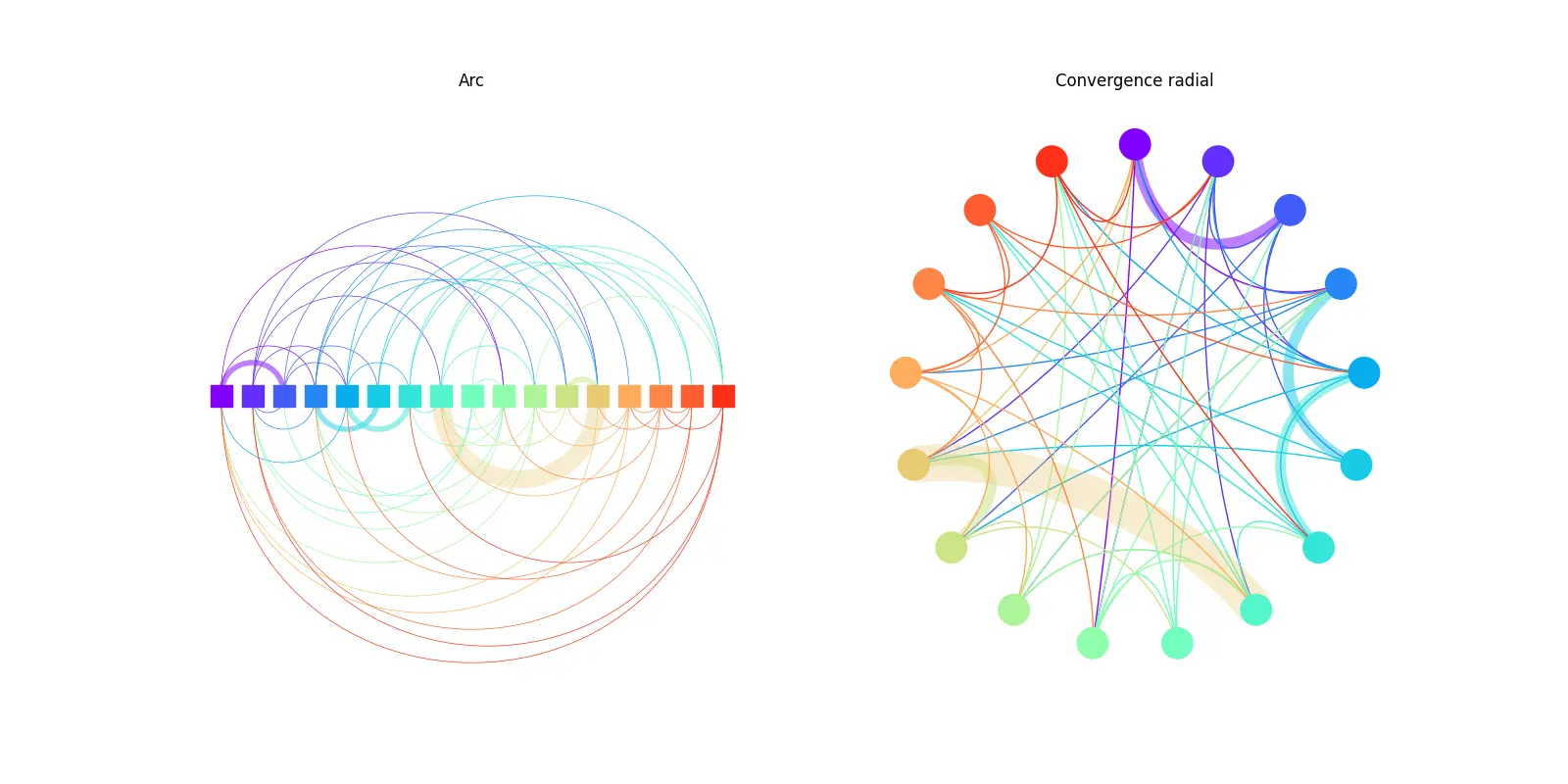
- 图弧图:左上弧图显示。
- 径向收敛(Convergence)图:右上径向收敛(Convergence)图可视化。
代码如下:
def test3():
# data
n = 17
indices = np.arange(n)
sel = lambda x: np.random.choice(x, n // 4)
mapa = np.array([sel(np.delete(indices, i)) for i in indices])
rede = indices[mapa]
# param
cmapArco = cm.get_cmap('rainbow')
fig, (axA, axB) = plt.subplots(1, 2)
# Arc
getPx = lambda x: x / (n - 1)
pontos = [Path.MOVETO, Path.CURVE4, Path.CURVE4, Path.CURVE4]
for i, e in enumerate(indices):
conx, cont = np.unique(rede[i], return_counts=True)
xo = getPx(i)
*cor, _ = cmapArco(i / n)
for cx, ct in zip(conx, cont):
xi = getPx(np.where(indices == cx)[0])
yoi = (xi - xo) * 2 ** 0.5
verts = [(xo, 0), (xo, yoi), (xi, yoi), (xi, 0)]
path = Path(verts, pontos)
patch = patches.PathPatch(path, facecolor='none', edgecolor=cor,
lw=0.5 * ct ** 3, alpha=1 / ct)
axA.add_patch(patch)
axA.scatter(indices / (n - 1), indices * 0, color=cmapArco(indices / n),
marker='s', s=256, zorder=2)
axA.set_title('Arc')
axA.set_xlim([-0.05, 1.05])
axA.set_ylim([-1.2, 1.2])
axA.axis('off')
# Convergence radial
getTheta = lambda x: 2 * np.pi * x / n
for i, e in enumerate(indices):
conx, cont = np.unique(rede[i], return_counts=True)
thetao = getTheta(i)
xo = np.sin(thetao)
yo = np.cos(thetao)
*cor, _ = cmapArco(i / n)
for cx, ct in zip(conx, cont):
thetai = getTheta(np.where(indices == cx)[0])
xi = np.sin(thetai)
yi = np.cos(thetai)
xm = (xo + xi) * 0.5
ym = (yo + yi) * 0.5
verts = [(xo, yo), ((xo + xm * 0.25) * 0.5, (yo + ym * 0.25) * 0.5),
((xi + xm * 0.25) * 0.5, (yi + ym * 0.25) * 0.5), (xi, yi)]
path = Path(verts, pontos)
patch = patches.PathPatch(path, facecolor='none', edgecolor=cor,
lw=ct ** 3, alpha=1 / ct)
axB.add_patch(patch)
axB.scatter(np.sin(getTheta(indices)), np.cos(getTheta(indices)),
color=cmapArco(indices / n), s=512, zorder=2)
axB.set_title('Convergence radial')
axB.set_xlim([-1.2, 1.2])
axB.set_ylim([-1.2, 1.2])
axB.axis('off')
plt.show()
5 终极法宝
看代码是不是一脸懵,很多童鞋估计还是不太理解贝塞尔曲线中控制点的作用…
😃
没关系,给大家提供一个网址,方便大家在线(online)查看不同控制点的效果示意图.
如下所示为第三节流(stream)动图的贝塞尔曲线示意图:
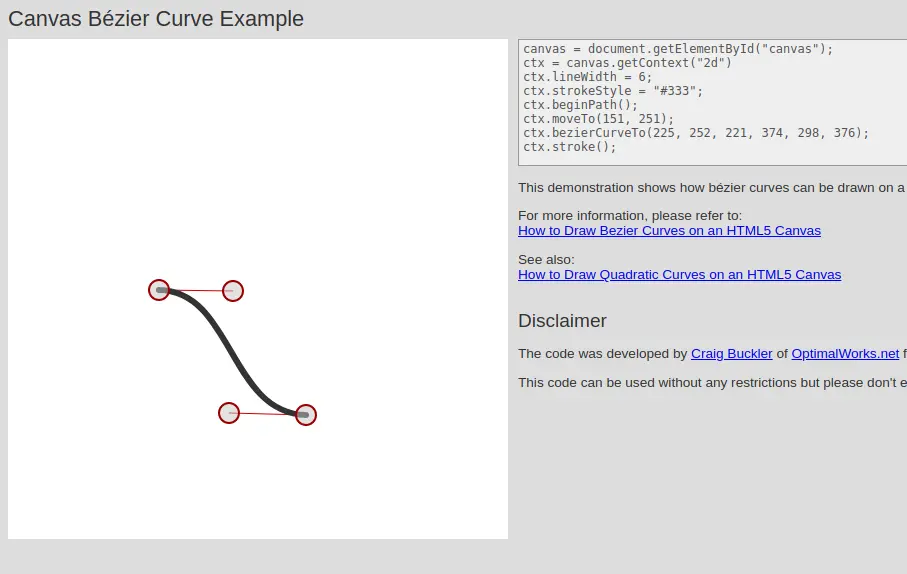
如下所示为第四节圆弧图的贝塞尔曲线示意图:
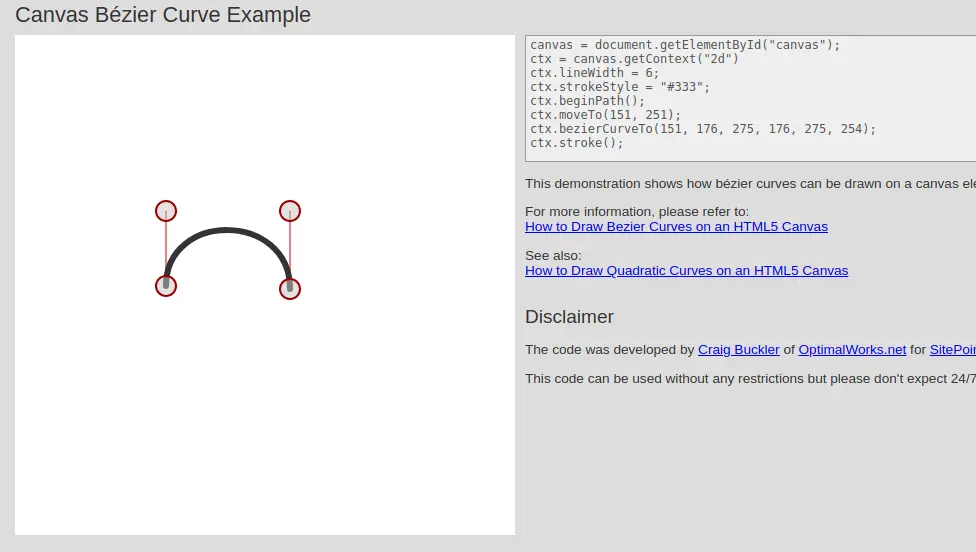
有了上述网站,你还可以根据这个网站设计多种path中的控制点的位置,来达到不同的显示效果.
Just have a try…
6 总结
本文详细地介绍了使用matplotlib画网络图、流(stream)动图和圆弧图的样例,并给出了相关可视化效果。
您学废了吗?
关注公众号《AI(人工智能(Artificial Intelligence))算法之道》,获取更多AI(人工智能(Artificial Intelligence))算法资讯。

注: 关注公众号,后台回复 path , 可获取完整代码
版权声明:本文为博主赵卓不凡原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
