python 数据挖掘算法

1、首先简述数据挖掘的过程

第 1 步：数据选择

可以通过业务原始数据、公共数据集、爬虫等方式获取。

第 2 步：数据预处理

数据极可能有噪音，不完整等缺陷，需要对数据进行数据标准化，方法有min-max 标准化， z-score 标准化，修正的标准z-score。

第三步：特征值数据转换

提取数据，使数据符合特定数据挖掘算法的分析模型。数据模型有很多，后面会详细讲解。

第 4 步：模型训练

选择一个好的数据挖掘算法来训练数据

第五步：测试模型+效果评估

主流方法有两种：

十折交叉验证：将数据集随机分割成十个等份，每次用9份数据做训练集，1份数据做测试集，如此迭代10次。十折交叉验证的关键在于较平均地分为10份。

N折交叉验证又称为留一法：用几乎所有的数据进行训练，然后留一个数据进行测试，并迭代每一数据测试。留一法的优点是：确定性。

第 6 步：模型使用

使用经过训练的模型对数据进行预测。

第 7 步：解释和评估

对数据挖掘后的信息进行分析和解释，并将其应用于实际工作领域。

2、主要的算法模型讲解 ——基于sklearn

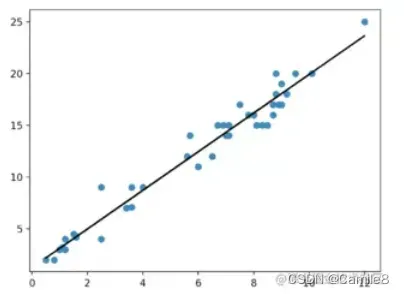
1）线性回归：希望所有点都落在直线上，所有点离直线的距离最近。首先假设好y=ax+b中a和b的值，然后计算每个数据点到这条直线上的距离总和，目的是要使这个总和最小！

from sklearn.linear_model import LinearRegression
# 定义线性回归模型
model = LinearRegression(fit_intercept=True, normalize=False, 
    copy_X=True, n_jobs=1)
"""
参数
---
    fit_intercept：是否计算截距。False-模型没有截距
    normalize： 当fit_intercept设置为False时，该参数将被忽略。 如果为真，则回归前的回归系数X将通过减去平均值并除以l2-范数而归一化。
     n_jobs：指定线程数
"""

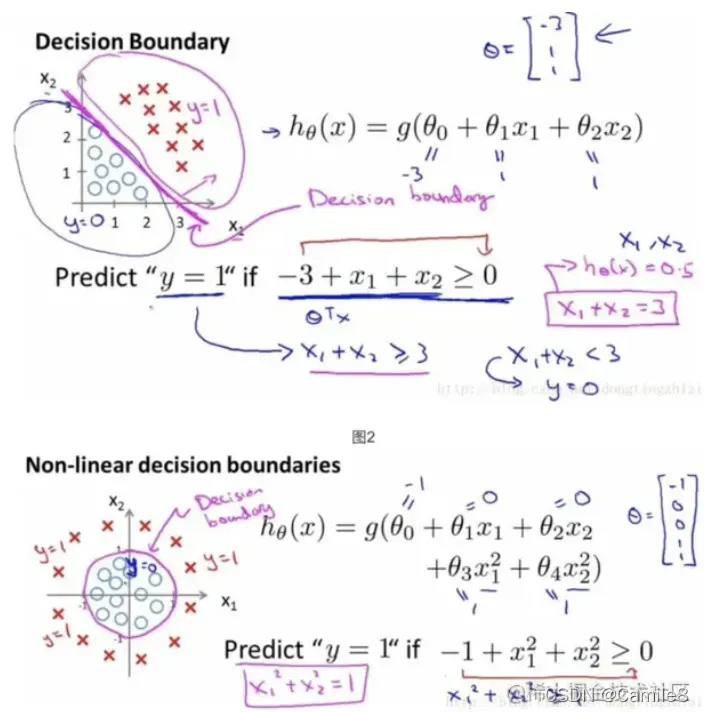
2）逻辑回归：二分算法，用于两分类问题。需要预测函数的“大概形式”，比如是线性还是非线性的。

如上所述，该数据集需要线性边界。不同的数据需要不同的边界。

from sklearn.linear_model import LogisticRegression
# 定义逻辑回归模型
model = LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0, 
    fit_intercept=True, intercept_scaling=1, class_weight=None, 
    random_state=None, solver=’liblinear’, max_iter=100, multi_class=’ovr’, 
    verbose=0, warm_start=False, n_jobs=1)

"""参数
---
    penalty：使用指定正则化项（默认：l2）
    dual: n_samples > n_features取False（默认）
    C：正则化强度的反，值越小正则化强度越大
    n_jobs: 指定线程数
    random_state：随机数生成器
    fit_intercept: 是否需要常量
"""

3）朴素贝叶斯算法NB：用于判断某件事的发生概率，我就曾用此算法做过舆情分类器。将一些语句变为01二维矩阵，计算词语的出现频率，从而判断语句的情感色彩是怎样的。

效率高，但有一定的出错概率

from sklearn import naive_bayes
model = naive_bayes.GaussianNB() # 高斯贝叶斯
model = naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
model = naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)
"""
文本分类问题常用MultinomialNB
参数
---
    alpha：平滑参数
    fit_prior：是否要学习类的先验概率；false-使用统一的先验概率
    class_prior: 是否指定类的先验概率；若指定则不能根据参数调整
    binarize: 二值化的阈值，若为None，则假设输入由二进制向量组成
"""

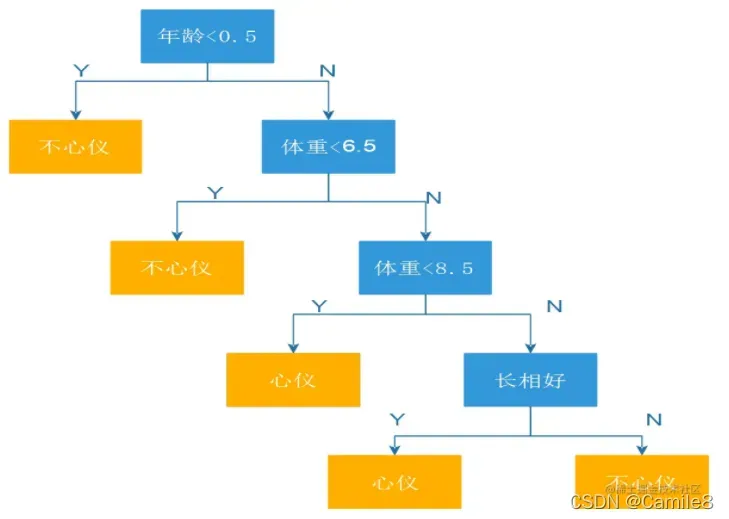
4）决策树DT：类似流程图的树结构，它使用分支方法来说明决策的每个可能结果。树中的每个节点代表对特定变量的测试 – 每个分支都是该测试的结果。

from sklearn import tree 
model = tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None, 
    min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, 
    max_features=None, random_state=None, max_leaf_nodes=None, 
    min_impurity_decrease=0.0, min_impurity_split=None,
     class_weight=None, presort=False)
"""参数
---
    criterion ：特征选择准则gini/entropy
    max_depth：树的最大深度，None-尽量下分
    min_samples_split：分裂内部节点，所需要的最小样本树
    min_samples_leaf：叶子节点所需要的最小样本数
    max_features: 寻找最优分割点时的最大特征数
    max_leaf_nodes：优先增长到最大叶子节点数
    min_impurity_decrease：如果这种分离导致杂质的减少大于或等于这个值，则节点将被拆分。
"""

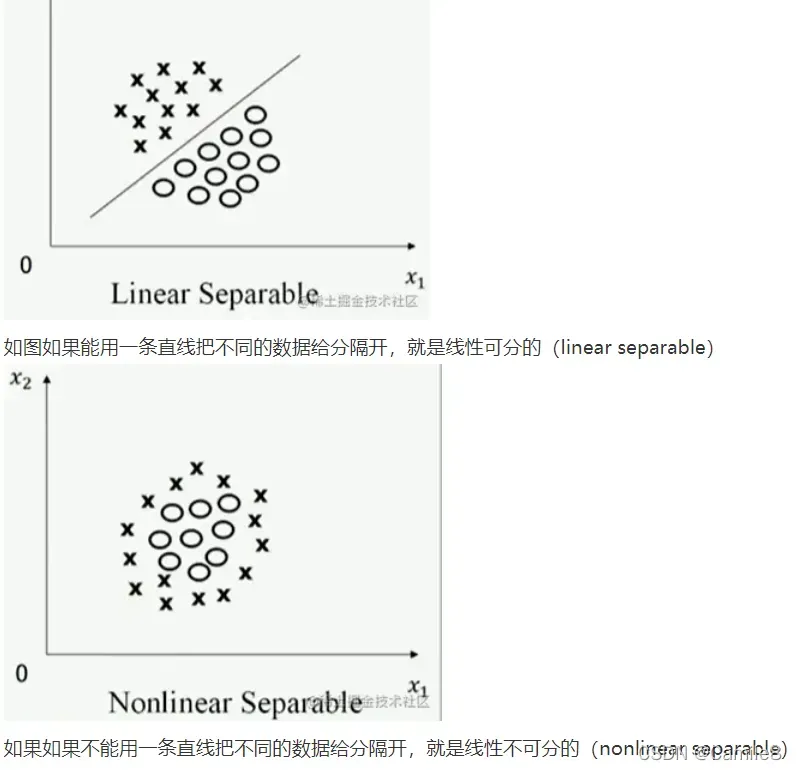
5）支持向量机SVM：就是判断线性可分不可分，能不能用直线分割两类数据！理论可以推广到三维，甚至思维以上的特征空间。三维使用平面来分隔数据，四维和四维以上因为人类无法直观的感知出来，所以画不出来，但是能分隔数据，存在这样的平面叫做超平面。

from sklearn.svm import SVC
model = SVC(C=1.0, kernel=’rbf’, gamma=’auto’)
"""参数
---
    C：误差项的惩罚参数C
    gamma: 核相关系数。浮点数，If gamma is ‘auto’ then 1/n_features will be used instead.
"""

6）k近邻算法KNN：采用测量不同特征值之间距离的方法对数据进行分类的一个算法。

给定一个样本的集合，这里称为训练集，并且样本中每个数据都包含标签。对于新输入的一个不包含标签的数据，通过计算这个新的数据与每一个样本之间的距离，选取前k个，通常k小于20，以k个剧里最近的数据的标签中出现次数最多的标签作为该新加入的数据标签。

K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中。（这就类似于现实生活中少数服从多数的思想）根据这个说法，咱们来看下引自维基百科上的一幅图：

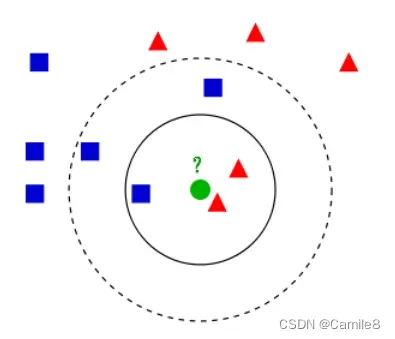
如果K=3，绿色圆点的最邻近的3个点是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。
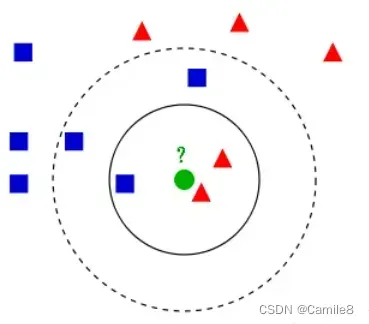
如果K=5，绿色圆点的最邻近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

from sklearn import neighbors
#定义kNN分类模型
model = neighbors.KNeighborsClassifier(n_neighbors=5, n_jobs=1) # 分类
model = neighbors.KNeighborsRegressor(n_neighbors=5, n_jobs=1) # 回归
"""参数
---
    n_neighbors： 使用邻居的数目
    n_jobs：并行任务数
"""

ps:我们在机器学习中一直会遇到两种问题，一种是回归问题，一种是分类问题。我们从字面上理解，很容易知道分类问题其实是将我们现有的数据分成若干类，然后对于新的数据，我们根据所分得类而进行划分；而回归问题是将现有数据拟合成一条函数，根据所拟合的函数来预测新的数据。这两者的区别就在于输出变量的类型。回归是定量输出，或者说是预测连续变量；分类问题书定量输出，预测离散变量。Po一张我在知乎上看到的一张图片，解释的很好：

3、sklearn自带方法joblib来进行保存训练好的模型

from sklearn.externals import joblib

# 保存模型
joblib.dump(model, 'model.pickle')

#载入模型
model = joblib.load('model.pickle')

参考链接：https://juejin.cn/post/6844903682576760846、https://juejin.cn/post/6844903513504530446、机器学习神器：sklearn的快速使用 – 掘金 (juejin.cn)、机器学习之逻辑回归(纯python实现) – 掘金 (juejin.cn)、

机器学习笔记5-支持向量机1 – 掘金 (juejin.cn)、

原文链接：https://blog.csdn.net/lipeitong333/article/details/123020866

python 数据挖掘算法

相关推荐