双指针
常⻅的双指针有两种形式,⼀种是对撞指针,⼀种是左右指针。 对撞指针:⼀般⽤于顺序结构中,也称左右指针。 • 对撞指针从两端向中间移动。⼀个指针从最左端开始,另⼀个从最右端开始,然后逐渐往中间逼 近。 • 对撞指针的终⽌条件⼀般是两个指针相遇或者错开(也可能在循环内部找到结果直接跳出循 环),也就是: ◦ left == right (两个指针指向同⼀个位置) ◦ left > right (两个指针错开) 快慢指针:⼜称为⻳兔赛跑算法,其基本思想就是使⽤两个移动速度不同的指针在数组或链表等序列 结构上移动。 这种⽅法对于处理环形链表或数组⾮常有⽤。 其实不单单是环形链表或者是数组,如果我们要研究的问题出现循环往复的情况时,均可考虑使⽤快 慢指针的思想。 快慢指针的实现⽅式有很多种,最常⽤的⼀种就是: • 在⼀次循环中,每次让慢的指针向后移动⼀位,⽽快的指针往后移动两位,实现⼀快⼀慢。
1. 移动零(easy)
「数组分两块」是⾮常常⻅的⼀种题型,主要就是根据⼀种划分⽅式,将数组的内容分成左右两部 分。这种类型的题,⼀般就是使⽤「双指针」来解决。 1. 题⽬链接:283. 移动零 2. 题⽬描述: 给定⼀个数组 nums ,编写⼀个函数将所有 0 移动到数组的末尾,同时保持⾮零元素的相对顺 序。 请注意 ,必须在不复制数组的情况下原地对数组进⾏操作。 ⽰例 1: 输⼊: nums = [0,1,0,3,12] 输出: [1,3,12,0,0] ⽰例 2: 输⼊: nums = [0] 输出: [0] 思路:用cur指针扫描整个数组,另一个dest指针记录非零序列最后一个位置,根据cur扫描过程,分类划分,实现数组的划分,这样使得[0,dest]都是非0元素,[dest+1,cur-1]都是0. 具体实现:class Solution {
public:
void moveZeroes(vector<int>& nums)
{
int cur = 0;
int dest = -1;
while(cur<nums.size())
{
if(nums[cur]!=0)
{
dest++;
swap(nums[cur],nums[dest]);
}
cur++;
}
}
};
核心思路就是,选用cur指向第一个元素的左边第一个元素,让dset往右边扫描,遇到0就走,遇到非零停,然后让cur++,目的是让他指向0,然后交换,循环的条件是cur<nums.size(),直到最后一个元素为止。
第一题:阶乘求和
 思路:
思路:
遍历n,然后item来存放每一项,并且后一项是在前一项的基础上进行相乘,值得说的是,这里你定义的变量不能是int否则不能拿满分,原因是int类型包含的范围小,当n很大的时候,阶乘之和可能超过这个范围,导致发生溢出,因此应该用更大数据类型,如long long类型
#include <iostream>
using namespace std;
// 计算阶乘
long long factorial(int n) {
long long result = 1;
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}
int main() {
int n;
cin >> n;
long long sum = 0;
for (int i = 1; i <= n; i++) {
sum += factorial(i);
}
cout << sum;
return 0;
}
第二题:完数的判断
 分析:
分析:
找出n内所有完数,那么就先遍历n,定义一个变量sum对它的因子进行求和,,因为因子是变化的这里这里定义一个数组将其全部存起来,然后判断sum与i是否相等输出即可
#include<stdio.h>
void PerfNumber(int n);
int main()
{
int N;
scanf("%d",&N);
PerfNumber(N);
}
void PerfNumber(int n)
{
for(int i=2;i<=n;i++)
{
int sum=0,k=0;
int a[100]={0};
for(int j=1;j<i;j++)
{
if(i%j==0)
{
sum+=j;
a[k]=j;
k++;
}
}
if(sum==i)
{
k=0;
printf("%d its factors are ",i);
while(a[k])
{
printf("%d ",a[k]);
k++;
} printf("\n");
}
}
return;
}第三题:字符串的输入输出处理
 思路:
思路:
解决这道题还是用istringstream来处理,并且定义了一个函数来实现字符串的切割。更方便处理字符串流的文本,并且注意当读取n的时候,要把末尾\n给去掉,可以用getchar也可以用cin.ignore(),然后是多组输入,这里用一个while循环,即一直读取str,当小于n时原样输出,大于时,输出字符串流。
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
using namespace std;
void stringSplit(string str); //这里加不加const都行,加上是因为编程习惯,这个符号在函数中不能修改
int main() {
int n, i = 0;
string str;
cin >> n;
getchar();
while (getline(cin, str)) {
if (i++ < n) {
cout << str << endl << endl;
}
else {
stringSplit(str);
}
}
return 0;
}
void stringSplit(string str) {
istringstream iss(str);
string receive;
while (iss >> receive)
{
cout << receive << endl << endl;
}
}第四题:线性筛求素数(了解即可)
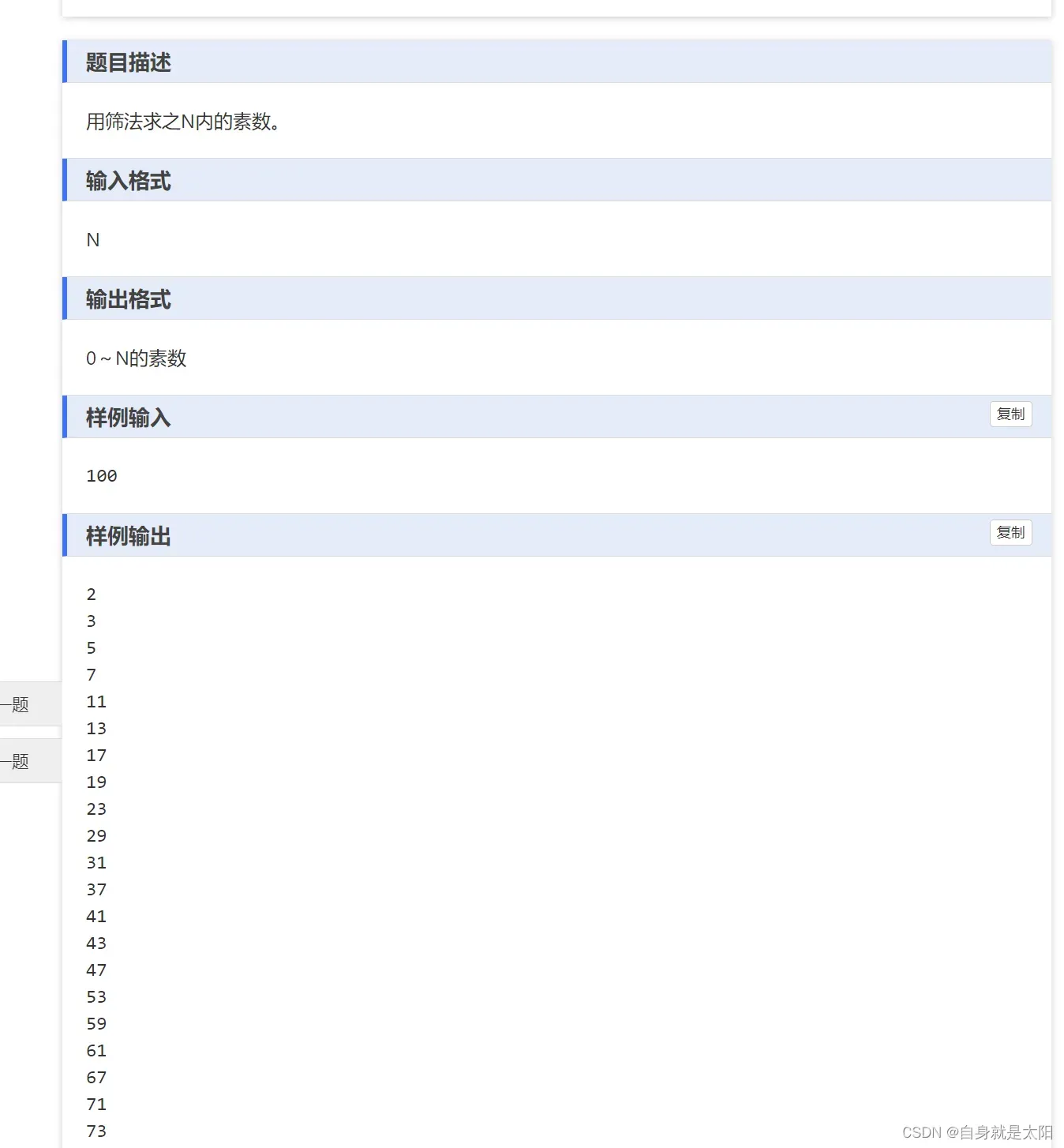
思路:这里用线性筛给大家实现,线性筛比普通遍历的方法效率更高,当处理一些比较麻烦的数据时,线性筛的作用就发挥出来了,核心在于去重,有兴趣博友可以去b站搜一下具体的讲解,这里不做阐述。
#include<bits/stdc++.h>
using namespace std;
//int isprime(int n);
const int maxn = 1e6;
int prime[maxn + 1];//放素数
bool isprime[maxn + 1];
int cnt = 0;//素数个数
void linesieve(int n)
{
memset(isprime, true, sizeof(isprime));//全部弄成true
for (int i = 2; i <= n; i++)
{
//遍历所有
if (isprime[i])
{
prime[++cnt] = i;
}
for (int j = 1; j <= cnt && prime[j] * i <= n; ++j)
{
isprime[prime[j] * i] = false;
if (i % prime[j] == 0)break;
}
}
for (int i = 2; i <= n; i++)
{
if (isprime[i])
cout << i << " " << endl;
}
}
int main()
{
int m;
cin >> m;
linesieve(m);
return 0;
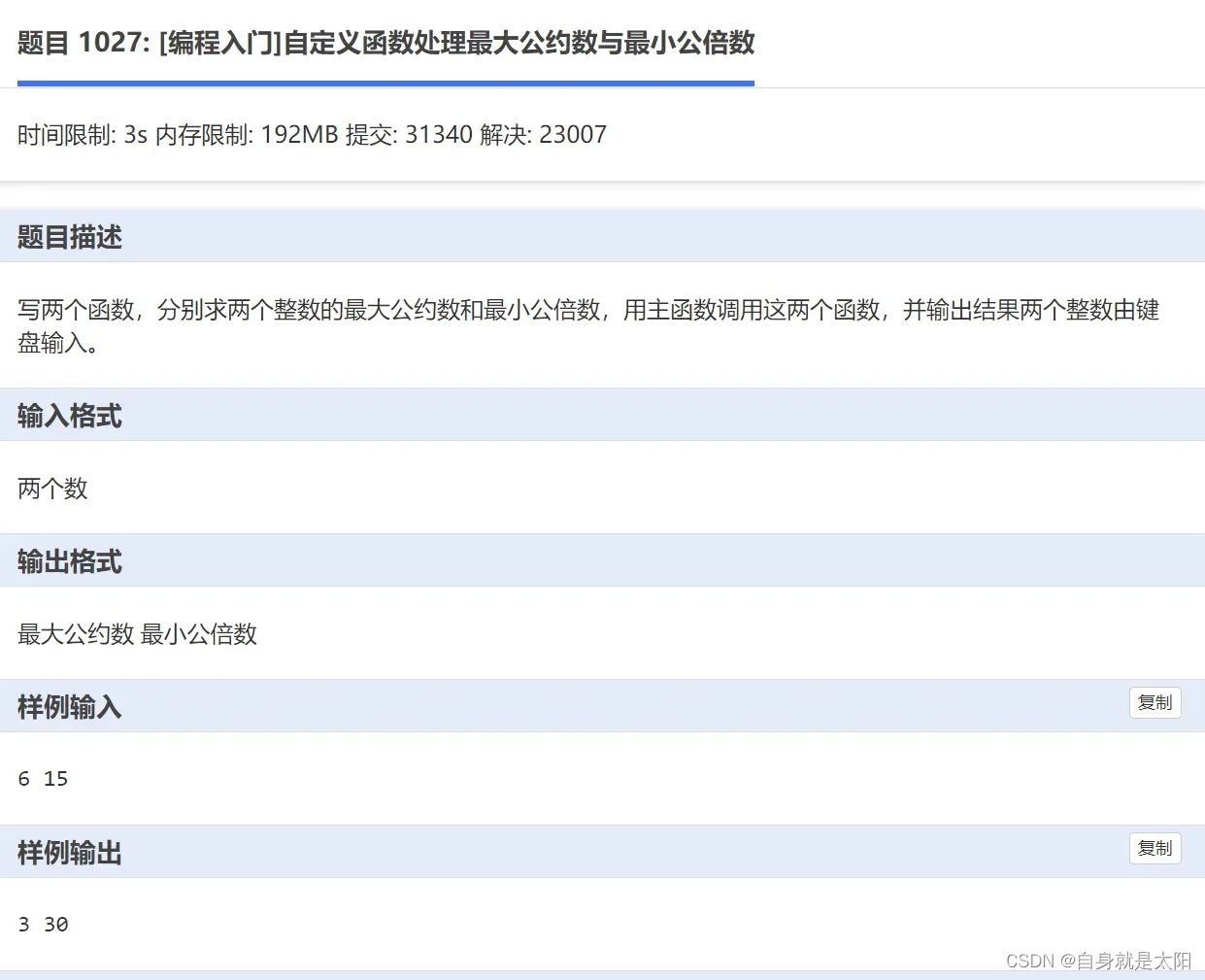
}第五题:自定义函数处理最大公约数与最小公倍数
 思路:
思路:
题目很简单,但也是基础说不定就考了呢,这里介绍辗转相除法求最大公约数和简单自增来求最小公倍数。求最大公倍数,首先要知道最大公倍数一定比这两个数都大,因此我们从a,b种大的数开始自增,直到这个数都能整除a,b,返回值即可。辗转相除法,有兴趣去b站学一下,这里不做阐述,给出代码,即先定义mod,每次循环,把b赋给a,把mod赋给b,直到b等于0跳出循环。
#include<bits/stdc++.h>
using namespace std;
int gcd(int a, int b);
int ret(int a, int b);
int main()
{
int a, b;
cin >> a >> b;
int gcd1 = gcd(a, b);
int ret1 = ret(a, b);
cout << gcd1 << " " << ret1;
return 0;
}
int gcd(int a, int b)
{
int mod;
while (b)
{
mod = a % b;
a = b;
b = mod;
}
return a;
}
int ret(int a, int b)
{
if (a > b)
swap(a, b);//确保a最大
int i;
for (i = a;; i++)
{
if (i % a == 0 && i % b == 0)
break;
}
return i;
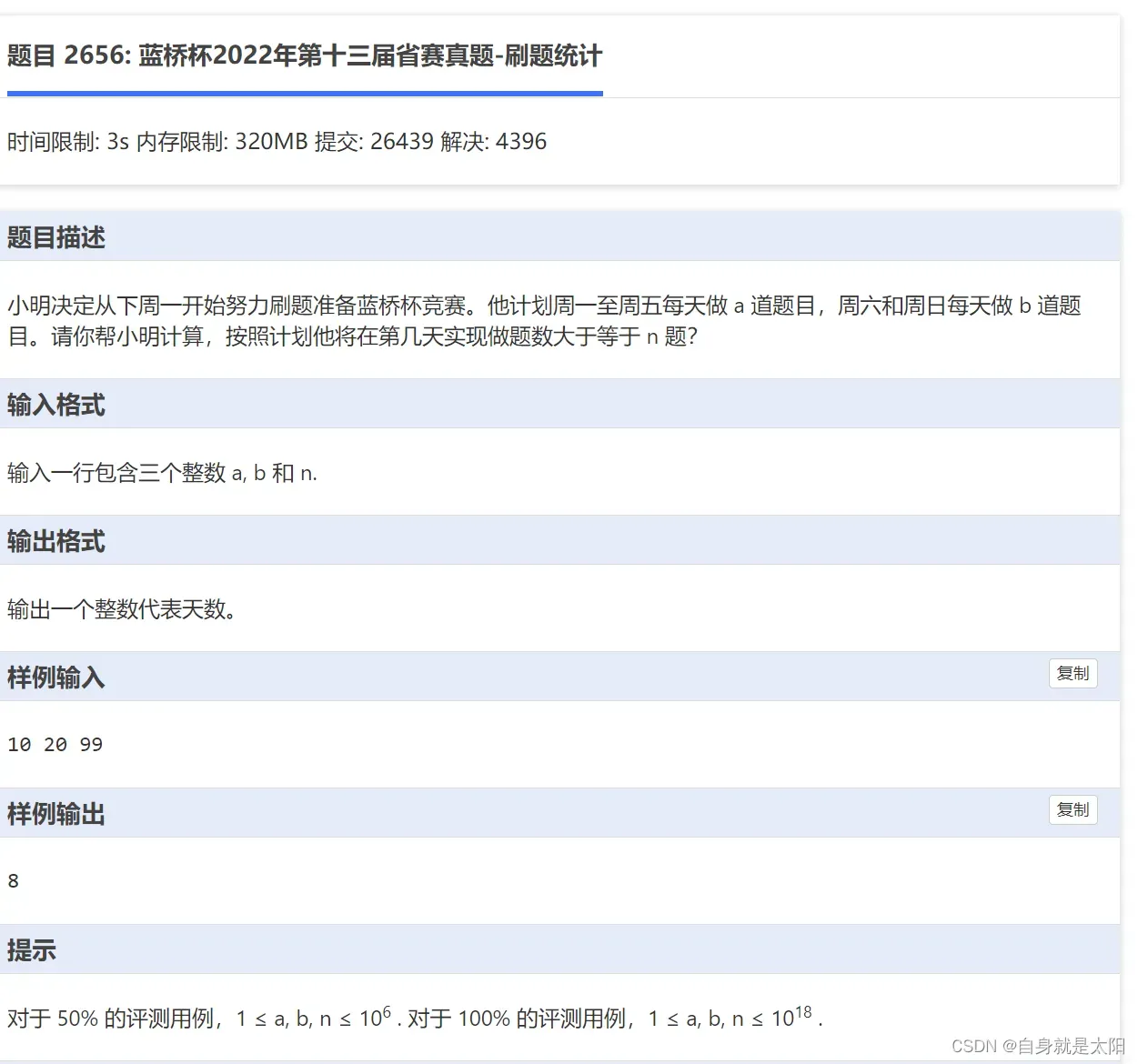
}第六题:蓝桥杯2022-刷题统计
 思路:
思路:
这道题虽然我只有80分,但还是想给大家介绍80 分的做法,就是学习这种分析,一步步整。首先我们要输出做题天数,并且周一到周五的做题量和周六周日不同,那么分开考虑,n为总题量,我们定义一个计数器,然后循环,条件为n>0.如果n<=0跳出循环,先遍历一周,i<5就每次n-a,并且在减之前判断n是否<0即可。
#include<bits/stdc++.h>
#pragma warning(disable:4996)
using namespace std;
const int N = 2022;
int main()
{
long long a, b, n;
scanf("%lld %lld %lld", &a, &b, &n);
int cnt = 0;
while (n>0)
{
for (int i = 0; i < 7; i++)
{
if (i < 5)
{
if (n <= 0)
break;
else
{
n = n - a;
cnt++;
}
}
else
{
if (n <= 0)
break;
else
{
n = n - b;
cnt++;
}
}
}
if (n <= 0)
break;
}
cout << cnt;
return 0;
}第七题:输出矩阵
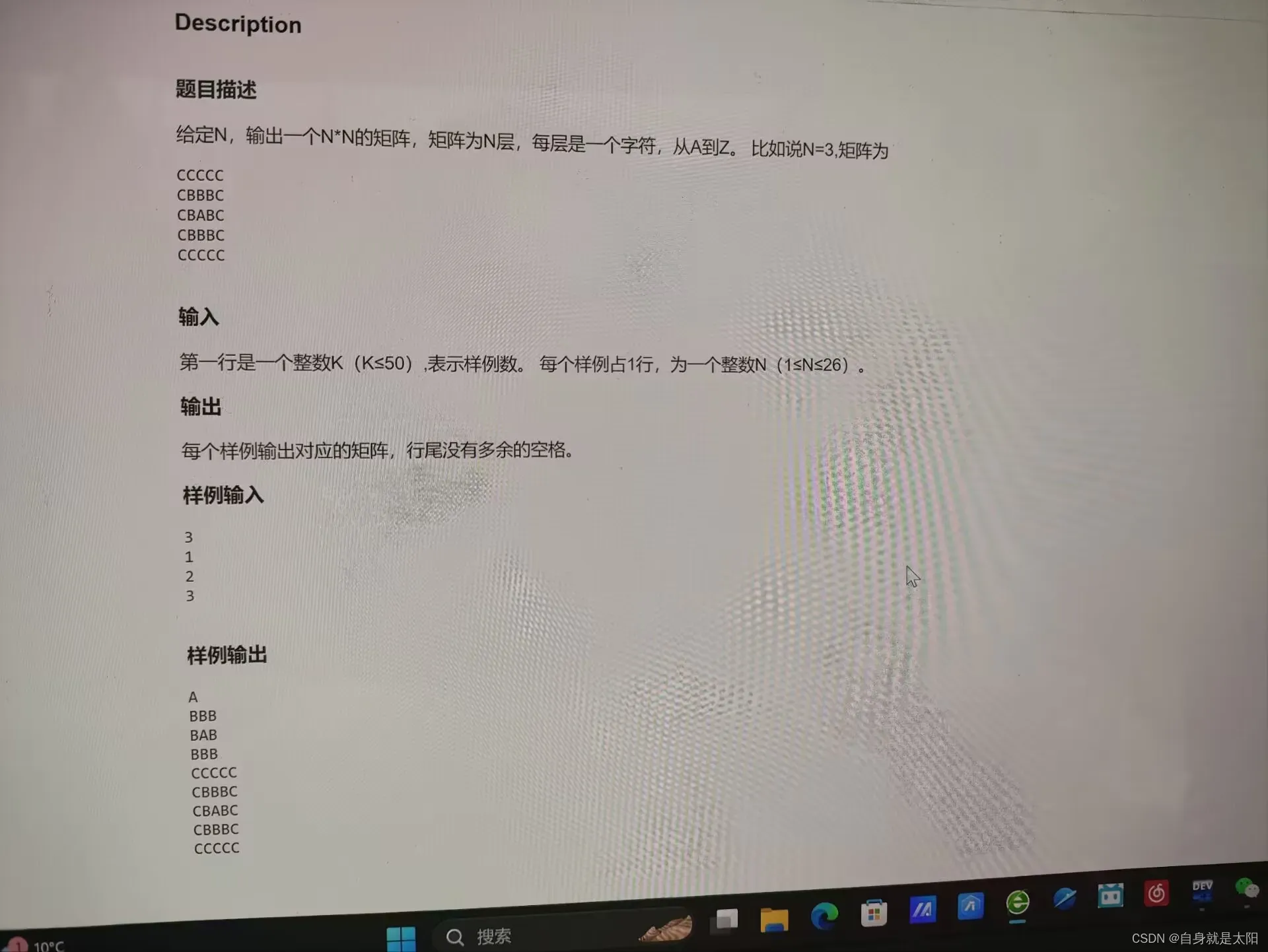
分析:这个题比较抽象,方法也很多这里给大家介绍一种很好理解的就是,先遍历二维数组先全部放一个字母然后通过控制层数行数列数再来另一个字母来覆盖我们已经设置的字母。比方说
假设输入的N为3,那么我们需要生成一个大小为5x5的矩阵。下面是每一层中填充字符的过程:
第0层:填充字符'A'
layer = 0,范围是从第0行到第4行,从第0列到第4列。
A A A A A
A A A A A
A A A A A
A A A A A
A A A A A
第1层:填充字符'B'
layer = 1,范围是从第1行到第3行,从第1列到第3列。
A A A A A
A B B B A
A B B B A
A B B B A
A A A A A
第2层:填充字符'C'
layer = 2,范围是第2行,第2列。
A A A A A
A B B B A
A B C B A
A B B B A
A A A A A
这样,通过不断递增layer和字符ch的方式,我们可以在每一层中正确地填充相应的字符。每次内层循环都会覆盖上一层填充的字符,所以最后得到了符合要求的矩阵。即layer是来控制层级,从最外层到最内层结束,每一层使用两个嵌套循环i和j来遍历,i控制行,从layer开始到n*2-1-layer-1结束,在每个位置(i, j)处,将字符ch赋值给matrix[i][j],完成对该层的字符填充。接着,逐渐增加字符ch的值,以便在下一层填充不同的字符。通过这种方式,代码会按照层级从外到内的顺序,依次填充不同的字符。
#include <iostream>
using namespace std;
int main() {
int N;
cin >> N; // 输入N
char matrix[101][101];
// 初始化矩阵
for (int i = 0; i < N * 2 - 1; i++) {
for (int j = 0; j < N * 2 - 1; j++) {
matrix[i][j] = 'Z';
}
}
// 填充字符
char ch = 'A';
for (int layer = 0; layer < N; layer++) {
for (int i = layer; i < N * 2 - 1 - layer; i++) {
for (int j = layer; j < N * 2 - 1 - layer; j++) {
matrix[i][j] = ch;
}
}
ch++;
}
// 输出矩阵
for (int i = 0; i < N * 2 - 1; i++) {
for (int j = 0; j < N * 2 - 1; j++) {
cout << matrix[i][j];
}
cout << endl;
}
return 0;
}
第八题:平方矩阵
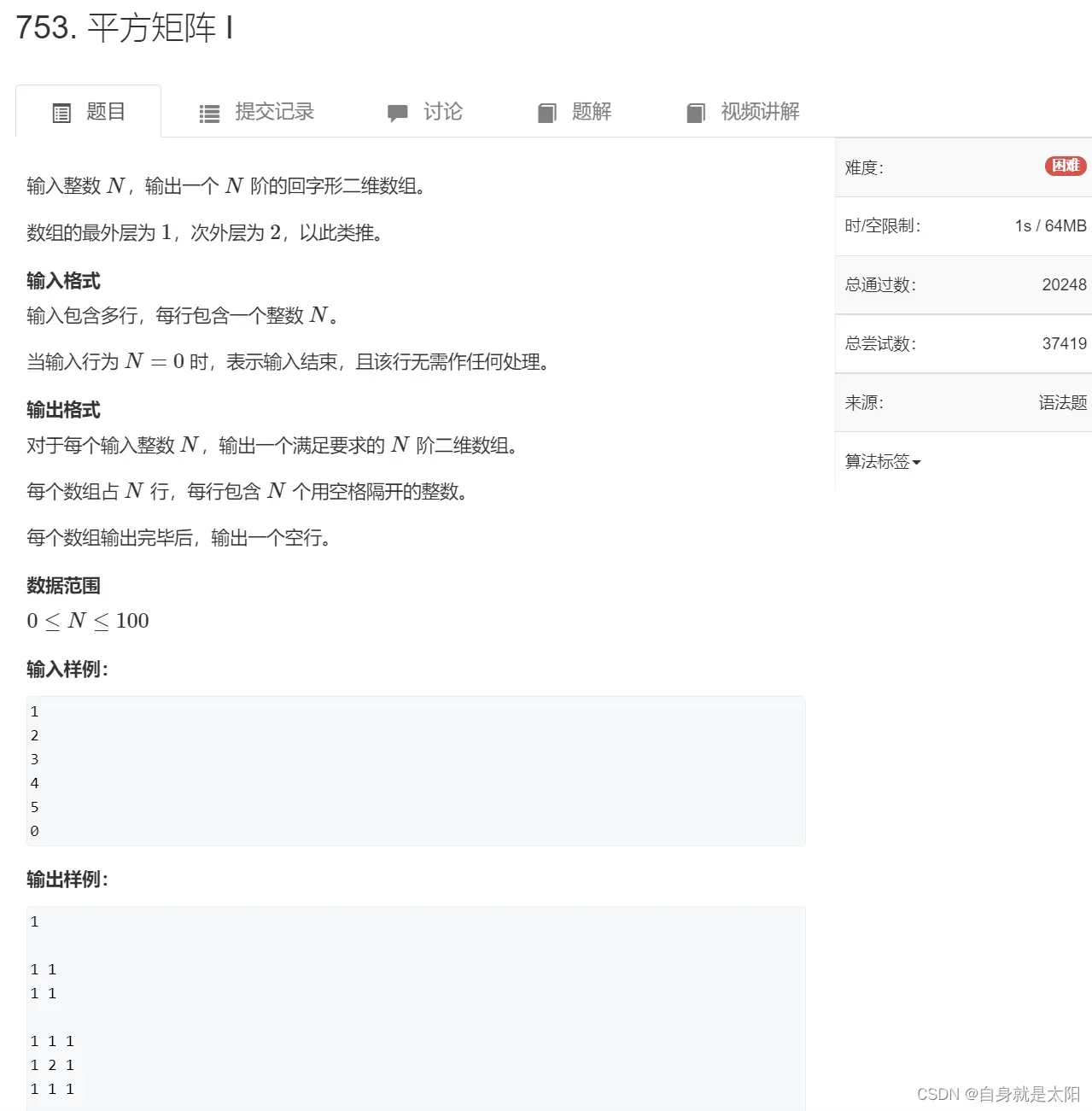
思路:乘热打铁,与上题类似,这道题应该如何处理,
#include <iostream>
using namespace std;
int main()
{
int N;
while (cin >> N, N)
{
int matrix[101][101];
// 初始化矩阵
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
matrix[i][j] = 1;
}
}
// 填充字符
int ch = 1;
for (int layer = 0; layer < N; layer++)
{
for (int i = layer; i < N - layer; i++)
{
for (int j = layer; j < N - layer; j++)
{
matrix[i][j] = ch;
}
}
ch++;
}
// 输出矩阵
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
cout << matrix[i][j] << " ";
}
cout << endl;
}
}
return 0;
}
文章出处登录后可见!
