目录
背景介绍
斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)
斐波那契数列(Fibonacci Sequence)又称黄金分割数列。
该数列指的是这样的一列数字:0、1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597、2584、4181、6765、10946、17711、28657、46368…
特别指出:第0项是0,第1项是第一个1。此数列从第2项开始,每一项都等于前两项之和。
在数学上,斐波纳契数列被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)。
在现代物理、准晶体结构、化学等领域,斐波纳契数列都有着直接的应用。美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载斐波那契数列此方面的研究成果。
斐波那契数列
-
斐波那契数列的发明者,意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci),生于公元1170年,卒于1250年,籍贯是比萨。他被人称作“比萨的列昂纳多”。
列昂那多·斐波那契于1202年研究兔子产崽问题时发现了此数列。设一对大兔子每月生一对小兔子,每对新生兔在出生一个月后又下崽,假若兔子都不死亡。问:一对兔子一年能繁殖成多少对兔子?
题中本质上有两类兔子:一类是能生殖的兔子,为大兔子;新生的兔子不能生殖,为小兔子;小兔子一个月就长成大兔子,求的是大兔子与小兔子的总和?

-
十二月时有大兔子144对,小兔子89对,共有兔子144+89=233对
从上表看出:
①每月小兔对数=上月大兔对数
②每月大兔对数等于上个月大兔对数与小兔对数之
综合①②两点可得:每月大兔对数等于前两个月大兔对数之和 如果用un表示第n月的大兔对数,则有un=un-1+un-2(n > 2)
每月大兔对数un排成数列为:1、1、2、3、5、8、13、21、34、55、89、144…
那么此组数列就称为斐波那契数列

END
斐波那契数列通项公式
-
递推公式:
斐波那契数列:0、1、1、2、3、5、8、13、21、34、55、89、144…
如果设F(n)为该数列的第n项(n∈N*),那么这句话可以写成如下形式:显然这是一个线性递推数列。
通项公式:
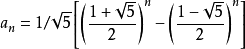
-
此公式又称为“比内公式”,是用无理数表示有理数的一个范例。

解法1:非数组+非递归
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a,b,c;
int main()
{
a=1;
b=1;
for(int i=1;i<=38;i++)//38的原因是已知两个数的值
{
c=a+b;//前一个值+前两个值
a=b;//值位置的变换
b=c;
}
printf("%lld",c);
return 0;
}解法2:数组+非递归
时间复杂度约为O(n)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=41;
ll num[maxn];
int main()
{
num[1]=1;
num[2]=1;
for(int i=3;i<=40;i++)
{
num[i]=num[i-1]+num[i-2];
}
printf("%d",num[40]);
return 0;
}解法3:非数组+递归
时间复杂度约为(2^n)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll step=0,cnt=0;
int Digui(ll step)
{
cnt++;
if(step==1||step==2)
{
return 1;
}
return Digui(step-1)+Digui(step-2);
}
int main()
{
Digui(40);
printf("%lld\n%lld",Digui(40),cnt);//答案 递归次数
return 0;
}
通过cnt计算发现,进行了非常多次数的递归,原因是我们进行了重复计算
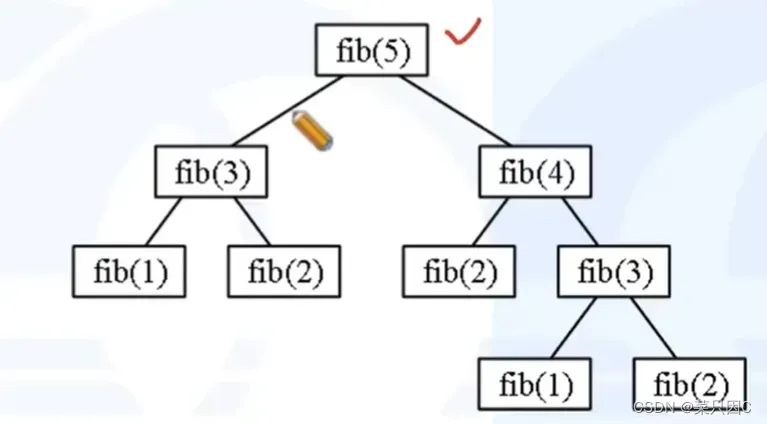
这样二叉树的结构导致进行了大量重复计算,这是我们特别不希望看到的,所以要进行记忆化
解法4:数组+递归
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=41;
ll num[maxn];
ll step=0,cnt=0;
bool vis[maxn];
int Digui(ll step)
{
cnt++;
if(step==1||step==2)
{
return 1;
}
if(!vis[step])
{
vis[step]=true;
num[step]=Digui(step-1)+Digui(step-2);
return num[step];
}
else
{
return num[step];
}
}
int main()
{
vis[1]=true;
vis[2]=true;
num[1]=1;
num[2]=1;
Digui(40);
printf("%lld\n%lld",Digui(40),cnt);
return 0;
}
这样计算次数会大大降低
文章出处登录后可见!
