近世代数是抽象代数的一个分支,是计算机科学和人工智能大数据的基础.
本文内容有点长,大家可以通过index来跳转到想要看的章节,第十章的总结在我的主页里下载
1.代数系
半群:满足结合律的代数系
交换半群:满足交换律的半群
群：判定方法有两种
method1
- 有单位元
- 有逆元
- 运算满足结合律
method2：
- 运算满足结合律
- 运算满足左右消去律
交换群(Abel群)：
定义:满足交换律的群
应用: 后面讲环的时候会用到Abel群,判定一个代数系(R,+,◦)是环:
- ( R, +)为一个 Abel群：
- ( R, ◦)为一个半群； ∀a, b, c ∈ R( a ◦ b) ◦ c = a ◦ ( b ◦ c）
- 乘法对加法满足左、右分配律： ∀a, b, c ∈ R a ◦ ( b + c) = ( a ◦ b) + ( a ◦ c) ( b + c) ◦ a = ( b ◦ a) + ( c ◦ a) 交换群可以衍生出很多好的性质
2.群的简单性质
群满足消去律
练习1答案方法的解释
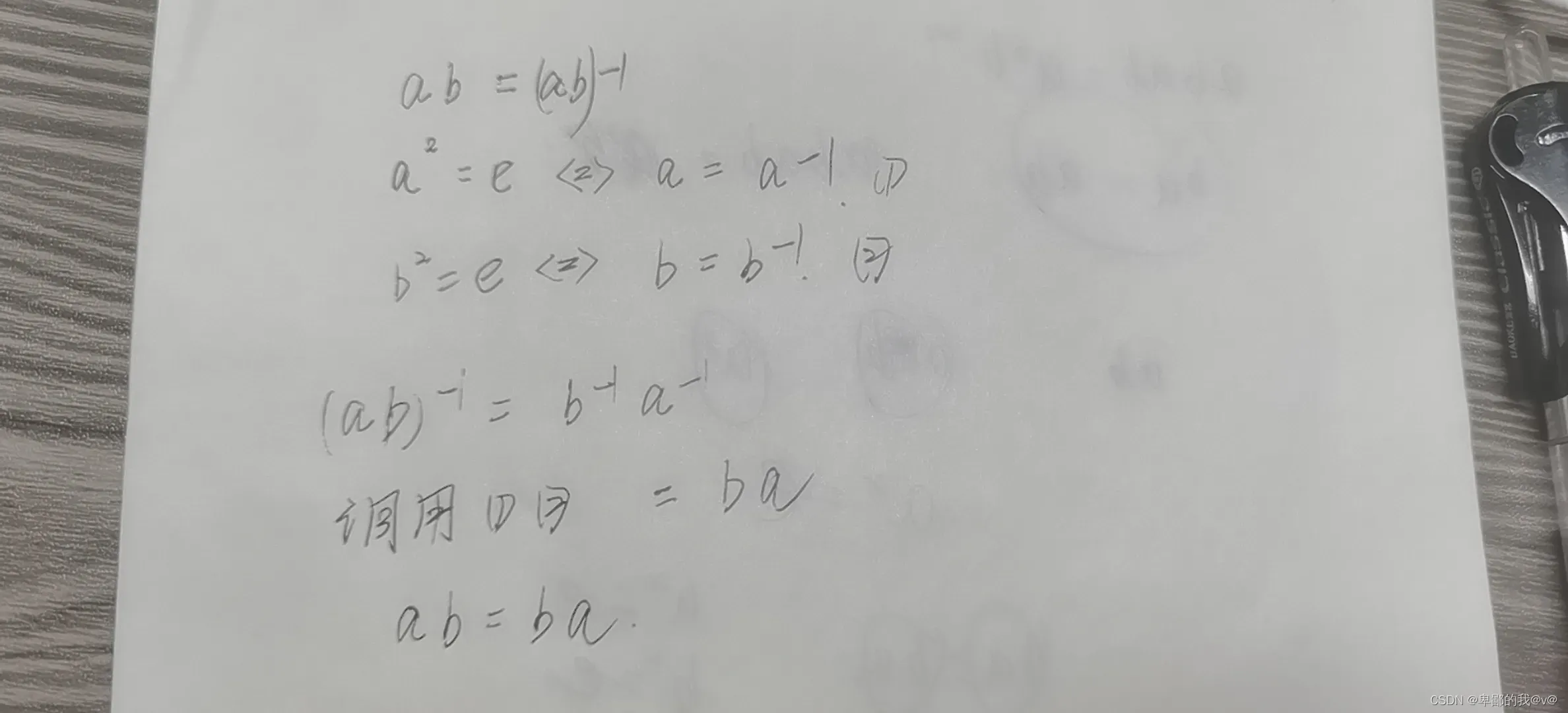
有限群的每个元素的阶不超过该有限群的阶。
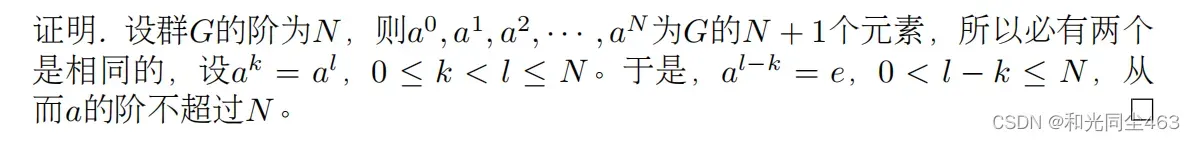根据群的阶判断元素的阶
练习6注释:根据练习4 5得到：阶大于2的元素成对出现则 |G| = 2n= 2k+l+1得到l是奇数 、
练习六也就是说偶数阶群2n一定存在一个阶为2的元素,也就是说一定存在n阶商群(后面会提到)
证明：一/二/三/四/五阶群是交换群
如何证明 五阶一下的群都是交换群 (利用后面的拉格朗日的定理 干掉前四个)
如何证明六阶群中 肯定存在一个三阶子群
3.子群 生成子群
子群
H是G的子群要满足三个条件
- H元素非空
- H中对于G中的运算封闭
- H是G的子集
eg:找出3次对称群的所有子群。
解 . (1)， { (1) ,(1 , 2) }， { (1) ,(1 , 3) }， { (1) ,(2 , 3) }， { (1) ,(123) ,(132) }， S3。判断子群的充要条件
同理在子环和子域中也有类似的证明
定理 ： 设( G1 , ◦)和( G2 , ∗)都是群， ϕ : G1 → G2， ∀a, b ∈ G1， ϕ( a ◦ b) = ϕ( a) ∗ ϕ( b)，证明： ϕ −1 ( e2)为 G1的子群，其中 e2为 G2的单位元素。
群G的任意多个子群的交还是G的子群
任一群不能是其两个真子群的并
1. 举例说明两个子群的并可以不是子群。
解 . S6 = { [0] , [1] , [2] , [3] , [4] , [5] }， { [0] , [2] , [4] }和 { [0] , [3] }为 S6的两个子群，但 { [0] , [2] , [4] }∪{ [0] , [3] } = { [0] , [2] , [3] , [4] }不是 S6的子群，因为[2] + [3] = [5] ∉ { [0] , [2] , [3] , [4] }。 2.设G1和G2为群G的两个真子群，证明：G1 ∪ G2为G的子群的充分必要条件是G1 ⊆ G2或者G2 ⊆ G1。 如果 G1 ⊆ G2或者 G2 ⊆ G1，则 G1 ∪ G2 = G2或 G1，此时显然 G1 ∪ G2为 G的子群。 如果 G1 ∪ G2为 G的子群，以下用反证法证明 G1 ⊆ G2或者 G2 ⊆ G1。 假设 G1 ⊈ G2并且 G2 ⊈ G1，则存在 g2 ∈ G2，但是 g2∉ G1，同时存在 g1 ∈ G1，但是 g1 ∉ G2。于是 G1为 G1 ∪ G2的真子集， G2为 G1 ∪ G2的真子集，易得 G1和 G2为 G1 ∪G2的真子群，由于任一群不能是两个真子群的并,矛盾。群G的中心C是G的可交换子群。
中心: 群G的元素a称为G的中心元素，如果a与G的每个元素可交换，即∀x ∈ G, ax = xa。G的所有中心元素构成的集合C称为G的中心。
不要忘记先证明他是一个群 形式有点像正规子群
生成子群
设 M为 G的一个非空子集， G的包含 M的所有子群的交称为由 M生成的子群，记为( M)。 有一点像细胞分裂
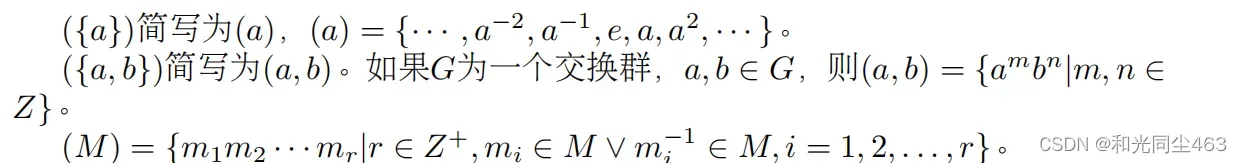推论:有限生成子群仍然是循环群
证明(Q, )的每个有限生成子群都是循环群？ – 知乎 (zhihu.com)
4.变换群 同构
同构:
设(G1, ◦)，(G2, ∗)为两个群。如果存在一个双射ϕ : G1 → G2，使得∀a, b ∈ G， ϕ(a ◦ b) = ϕ(a) ∗ ϕ(b), 则称群G1与G2同构，记为G1 ≅ G2。ϕ称为从G1到G2的一个同构。
同构和同态区别和联系:
- 都满足那个等式
- 不同:同态不一定要求是双射
变换群
对称群:设 S为一个非空集合，从 S到 S的所有双射构成的集合对映射的合成构成一个群，称为 S上的对称群，记为 Sym( S)。当 S = { 1 , 2 , · · · , n}时， Sym( S) = Sn。 变换群:Sym( S)的任意一个子群称为 S上的一个变换群。 Sn的任意一个子群称 为一个置换群。定理:任何一个群都同构于某个变换群。（Caley定理)
推论:任意一个 n阶有限群同构于 n次对称群 Sn的一个 n阶子群，亦即任意一个 有限群同构于某个置换群。练习:
- 证明一个群是一个变换群
- 证明是同构,关键是找到一个映射,先证明是一个映射,再证明是一个满射,再证明符合同构的等式。
5.循环群
循环群的定义:
如果G是由其中的某个元素a生成的，即G = (a) = {· · · , a−2 , a−1 , e, a, a2 , · · · }
- 整数加法群(Z,+)为循环群,其生成元为1。
- 模n同余类加群Zn = { [0], [1], · · · , [n − 1]}为一个阶为n的有限循环群,其生成元为[1]。
循环群的阶:
循环群的同构:
- 无穷循环群同构于整数加群(Z, +)，即如果不计同构，无穷循环群只有一个，就是整数加群；
- 阶为n的有限循环群同构于模n同余类加群(Zn, +)，即如果不计同构,n阶循环群只有一个，就是模n同余类加群。
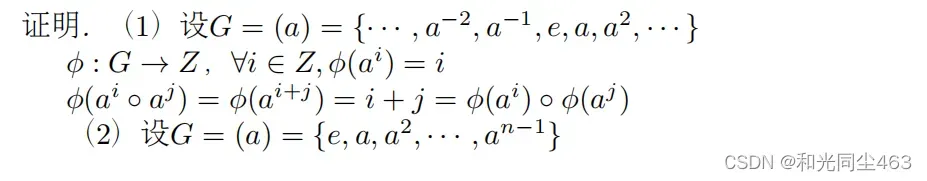
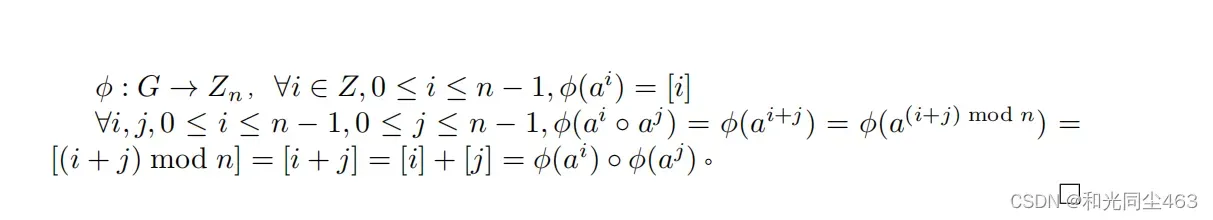这个定理告诉我们可以以整数加群和模n同余的整数加群为为媒介,证明两个子群同构
example
循环群子群的阶:
循环群的性质
- 循环群仍然是交换群 原因 循环群中的每一个元素都可以表示成a的多少次方，那么a^(i+j) = a^(j+i)显然是一个交换群
- 循环群的子群仍然是循环群
-
循环群的子群仍然是该循环群的正规子群
最大公约数
d为 a和 b的最大公约数表示为d=( a, b) 两个定理- 设a, b ∈ Z，a和b不全为0，则∃m, n ∈ Z使得(a, b) = ma + nb。
- 设 a, b ∈ Z， b > 0， a = qb + r，0 ≤ r < b，则( a, b) = ( b, r)。
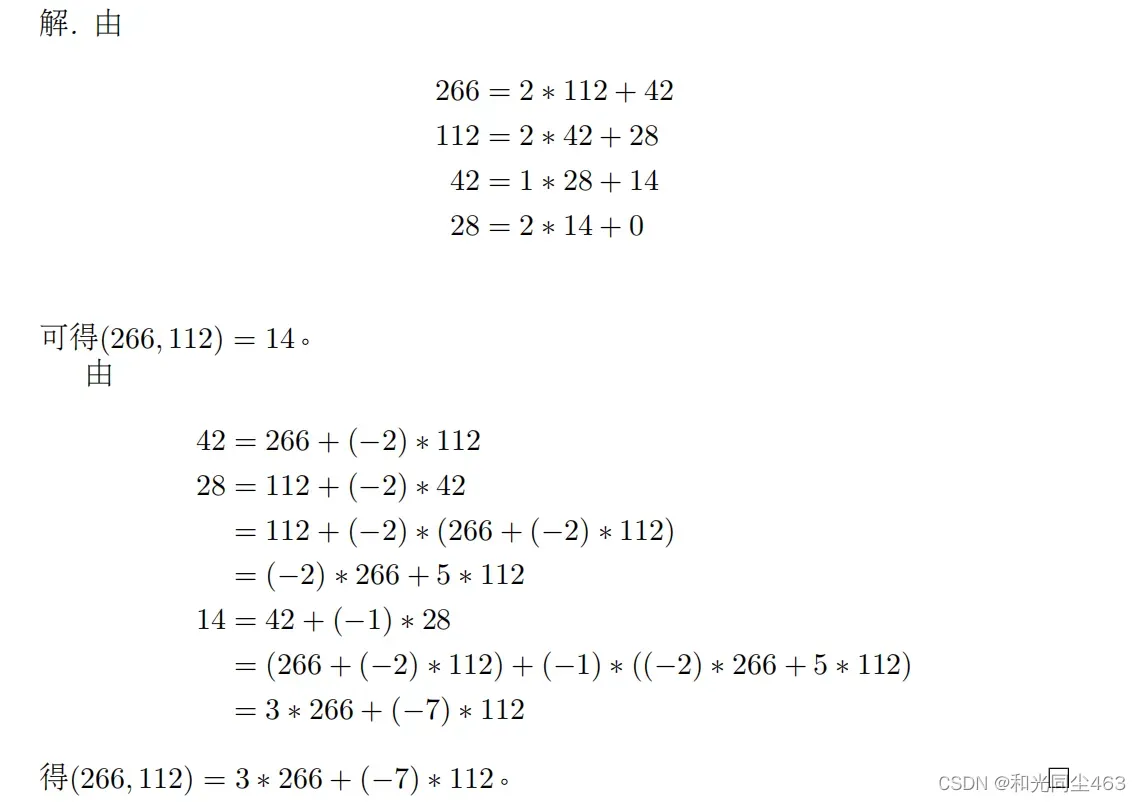
循环群的阶和最大公约数
子群的陪集 拉格朗日定理
Concept: 群子集的乘法
- AB = { ab|a ∈ A且 b ∈ B}
- ∀g ∈ G, A ∈ 2 G, { g}A简写为 gA，即 gA = { ga|a ∈ A}。 A{ g}简写为 Ag， 即 Ag = { ag|a ∈ A}。
- 设 G为一个群，则 ∀A, B, C ∈ 2 G，( AB) C = A( BC)。
Concept:陪集定义和性质
定义:
设 H为群 G的一个子群， a ∈ G，则集合 aH称为子群 H的一个左陪集, Ha称为 H的一个右陪集。性质:
- 设H为群G的一个子群，则∀a ∈ G，aH = H的充分必要条件是a ∈ H。
- 设 H为群 G的一个子群，则 ∀a, b ∈ G， aH = bH的充分必要条件是 a ^−1 b ∈ H。
- 子群的不相交性:设 H为群 G的一个子群，则 ∀a, b ∈ G， aH = bH或者 aH ∩ bH = φ。
- 等容量性:设 H为群 G的一个子群，则 ∀a, b ∈ G， |aH| = |bH|。
- 划分性:设H为群G的一个子群，则H的所有左陪集构成的集合为G的一个划分。
证明:参见讲义 第二条证明较为麻烦↓ ↓ ↓ ↓
拉格朗日定理
指数的定义:
设H为群G的一个子群，如果H的所有不同的左陪集的个数为有限数j则称j为H在G中的指数，记为j = [G : H]，否则称H在G中的指数为无穷大。
拉格朗日定理及推论:
设 G为一个有限群， H为 G的一个子群，则 |G| = |H| · [ G : H]。推论*3:
- 有限群中每个元素的阶都能整除该有限群的阶。
- 如果群的阶是素数,则该群是一个循环群。
- 设 G为一个群，则 ∀a ∈ G， a^|G| = e。
推论*2:
- 设 H为群 G的一个子群， Sl为 H的所有左陪集构成的集合， Sr为 H的所有右陪集构成的集合，则 |Sl | = |Sr|。
备注:
- 【a】p-1 = [1]是因为推论3 这个是要证明一个运算在一个群里
- 思考是否可以用群的另外一种判断方法来证明:证明结合律和左右消去律。
正规子群 商群
有了陪集和群子集乘法的概念,我们引入正规子群和商群。
简单复习
群运算:
其中对于定理三我们比较难理解
判断两个子群的乘积是否也是子群
正规子群
引入:
在上一节中我们学习了子群的乘法,但和映射类似,子群的乘法不一定满足交换律,例如
正规子群定义:
设 H为群 G的子群，如果 ∀a ∈ G， aH = Ha，则称 H为 G的正规子群。正规子群等价命题:
证明： 3-4相对麻烦
商群
引入(可以不用看)
就是证明代数系统是一个群
定义和形式化举例
定义:群G的正规子群H的所有左陪集构成的集族,对群子集乘法构成的群称为G对H的商群,记为G/H。
- 商群其实就是上面提到拉格朗日对于G的划分
- 商群是对集族进行运算而不是集合
- 每个商群划分的元素都是互不相交的
形式化举例
练习:
没啥多说的直接看吧
同态的基本定理
引入同态是为了消弱同构的条件 同态和同构差别就在于是否一定是双射
- 同态不一定是双射
- 单射叫单同态，满射叫满同态注意符号怎么写
同态定义
性质
两个定理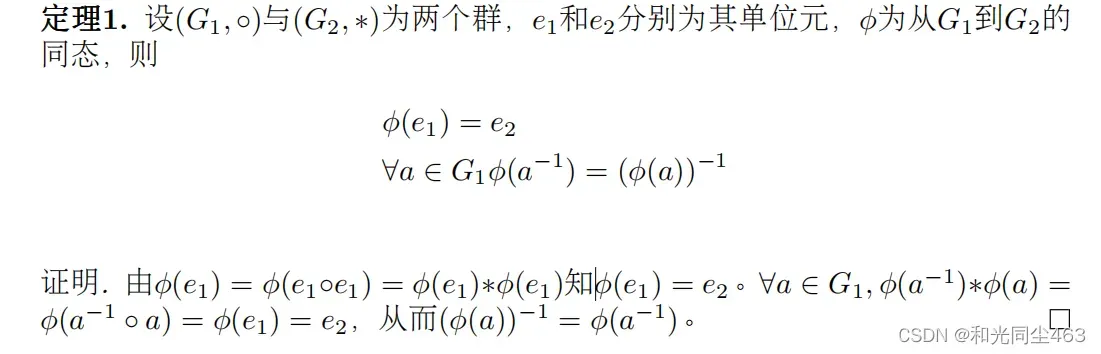
同态的替身和原同态关系
证明方法见笔记
同态的核
定义
同态像就是像集中能够被映射到的元素组成的集合。而同态核就是定义域集合中所有像为幺元的元素组成的集合。同态的核是衡量同态单射的程度。
特殊的同态核
这里需要注意的是先要验证是一个同态 因为只说了 他是一个映射 不一定满足那个同态表达式
同态基本定理
练习
环 体 域
有些符号打字太麻烦了 直接看我写的latex
定义
环
体
交换环 /域
子环/子域
判断子环的条件
减法 类似于加法的逆
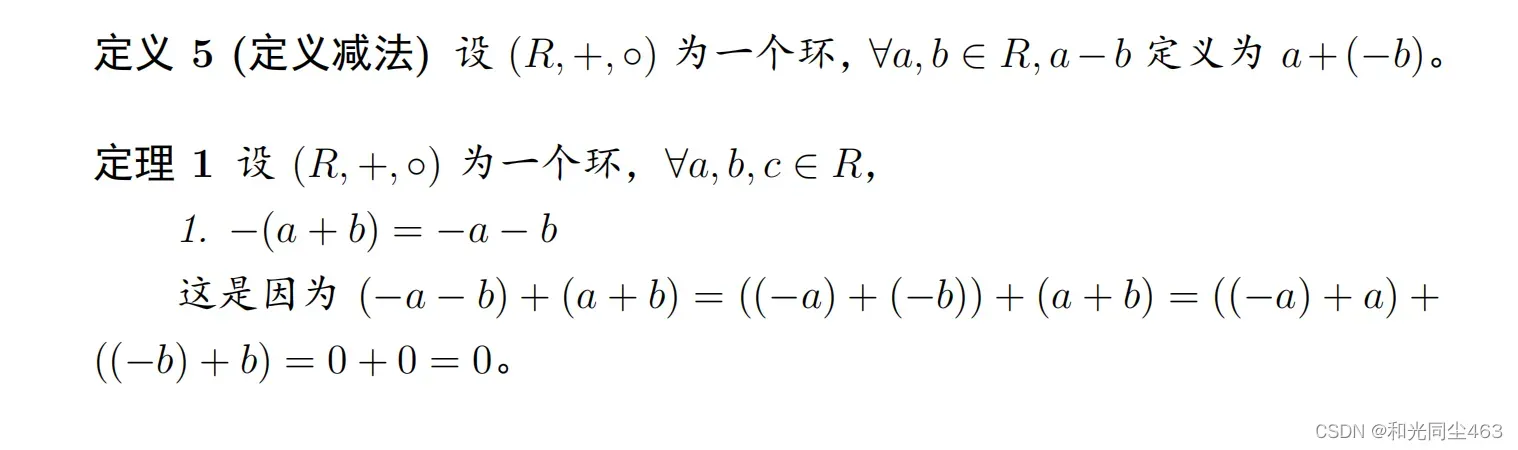
子环
子体/子域
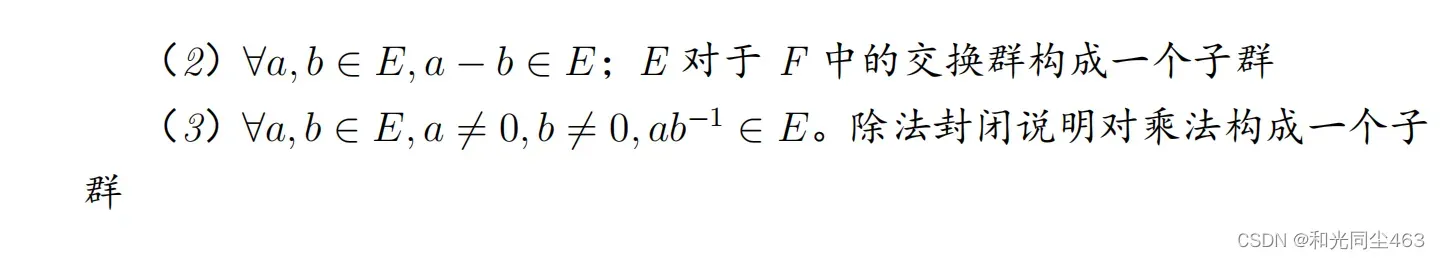
举例:
零因子环
零因子
无零因子环
判断无零因子环的充分必要条件(数理逻辑谓词证明方法)
判断无零因子环的充分必要条件
有限环和体的关系
练习
做题中遇见的问题和技巧
- 通过结合律和消去律 证明代数系是群 必须是有限群的充要条件
- 群G的中心是G的子群
- 偶数阶群一定至少存在一个阶为2的元素
- 如果一个n阶有限群中有一个元素的阶等于该有限群的阶n,那么这个群是一个循环群
- 如果两个数最大公约数是d,则存在非零整数m,n,使得,ma+nb=d
- 同构的两个群阶数相等
- 循环群一定是一个交换群 循环群的子群是原来群的正规子群
- 如果一个群的阶是素数那么这个群一定是循环群(拉格朗日) 进而也是一个交换群特殊的2阶群是循环群也是交换群
- 三阶群是交换群 四阶群也是交换群 证明往上翻
- H为G的正规子群 ah不一定等于ha ah = ah1
- 指数为2的子群是正规子群
- 证明两个集合乘法仍然是原来的子群只需证明AB = BA
- 证明G\H是商群的时候一定先说明H是正规子群
- 商群G\H的单位元是H,所有的元素(元素是集合)要么相等要么互不相交
- 证明同态的时候有的时候先要说明是一个映射 就是证明任意的a=b f(a)=f(b)相同的元素映射到相同的位置
- 同态的核只是相对于满同态来说 他是用来衡量同态映射的单射程度
- {e}是任何群的正规子群 这在同态的证明和同态核中有一部分的应用
- 证明环是第一个是Abel群 第二个是半群 不要搞混
1.证明是商群必须证明是正规子群
q:请问不是交换群 可不可以说明他有一个n阶商群 [G:H]= n和商群的阶是n是一回事么
a:商群必须是正规子群左陪集构成的集族 所以不是一回事
2.
使用反证法
3. 利用分类讨论的思想来做题
4.利用找特殊的方法
找出一个例子
5.利用已知条件进行一个”构造”的方法
关键是在3->2的推导
6.这个题虽然也是课后题 了解一下就好 拓展一下思路
.类比的思考 比如这个题 解答版能不能把那个定理推广到右陪集
8.拉格朗日定理的拓展
红笔的原因 因为H是是A的子集，所以H中元素与A构成的陪集就是A 详见任世军老师的网课
9.存在性问题
六阶群 一定存在一个三阶子群
2n阶交换群一定存在一个n阶商群
文章出处登录后可见！
