目录
前言:
前文快速排序采用了递归实现,而递归会开辟函数栈帧,递归的深度越深,占用栈区的空间就越大,栈区的大小一般是8M,10M,当递归深度足够深时,栈区的空间就会被用完,导致栈溢出,此时需要将递归改为非递归更加稳妥,本篇继续详细解读快排的非递归实现,归并排序,计数排序;
快速排序
快速排序非递归实现
- 采用递归实现快速排序时,而递归就是不断调用单趟排序函数的功能,若不采用递归,什么可以实现不断调用单趟排序函数的功能?
- 循环;
- 循环只要满足循环条件,就会不断调用单趟排序函数的功能,但是每次递归调用时单趟排序函数的参数是变化的,而循环条件确是一成不变的,递归会在栈上建立函数栈帧,而函数栈帧里面存放下次调用该函数的参数,若采用非递归,那我们就必须把每一次循环的参数记录下来,供单趟排序使用,如何解决?
- 使用顺序栈或者链式栈记录每次函数参数,栈的实现采用动态内存开辟,存储空间是堆区开辟的空间,堆区大小可达2G;
快速排序非递归实现步骤:
- 创建一个栈,将整个序列的起始位置和结束位置入栈;
- 当栈不为空时,弹出栈顶元素,取出该区间的起始位置 left 和结束位置 right;
- 对该区间进行划分,获取划分点 keyi;
- 如果keyi左边还有元素,将左半部分的起始位置left和结束位置keyi-1入栈;
- 如果keyi右边还有元素,将右半部分的起始位置keyi+1和结束位置right入栈;
- 重复步骤2-5,直到栈为空;
- 栈的特性为后入先出,先将待排序序列的右边界 right入栈,后将待排序序列的左边界left入栈;出栈时(获取栈顶元素)就可以先取到左边界值left ,后取到右边界值right;
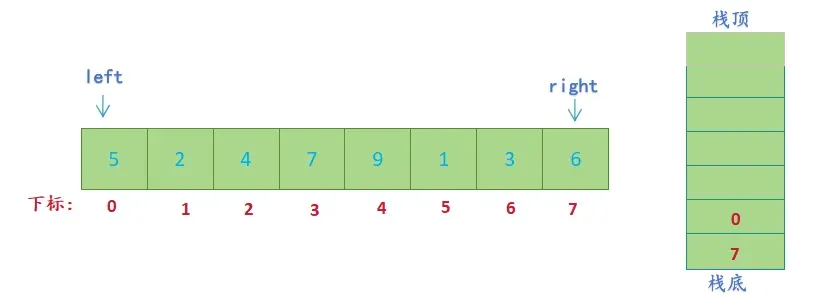
- 先获取栈顶元素,然后出栈,先取到0给left,后取到7给right,进行单趟排序(hoare版本)

- 区间被划分为【left,keyi-1】 U keyi U 【keyi+1, right】(left=0, keyi-1=3,keyi+1=5,right=7),为了先处理划分后的左子序列,先将右子区间的边界值right keyi+1分别入栈(先入right,后入keyi+1) ,然后将左子区间的边界值keyi-1,left分别入栈(先入keyi-1, 后入left);
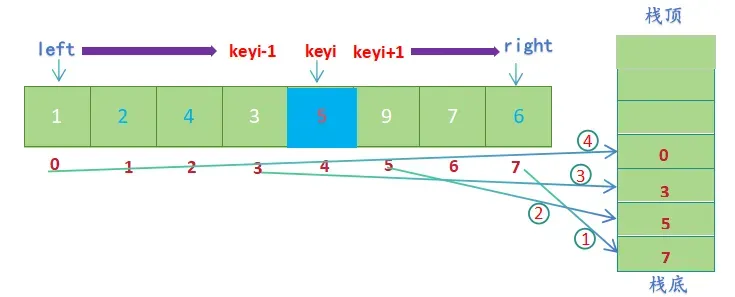
- 先取栈顶元素,然后出栈,先取到的元素给left ,后取到的元素给right (left=0, right=3), 进行单趟排序(hoare版本);
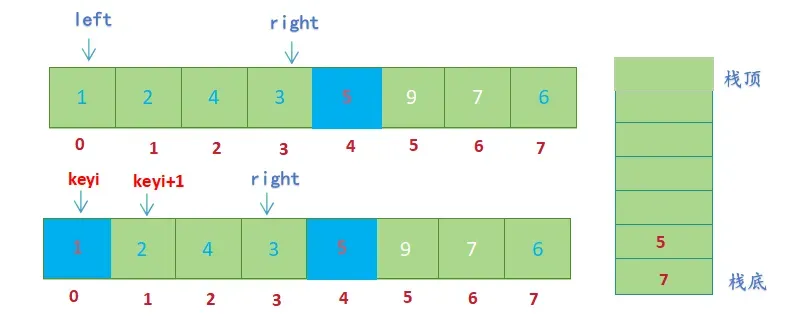
- keyi左边没有元素,keyi右边还有元素,将右半部分的起始位置keyi+1和结束位置right入栈(right先入栈,keyi+1后入栈)

- 先取栈顶元素,然后出栈,先取到的元素给left ,后取到的元素给right (left=1, right=3), 进行单趟排序(hoare版本);
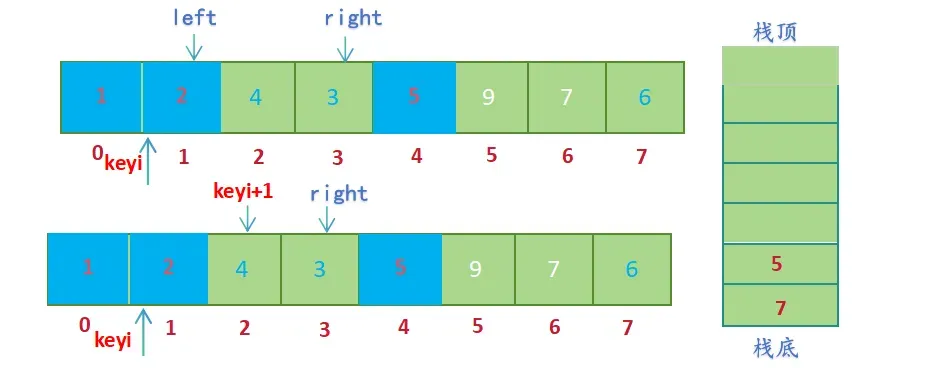
- keyi左边没有元素,keyi右边还有元素,将右半部分的起始位置keyi+1和结束位置right入栈(right先入栈,keyi+1后入栈)


- 左子区间全部被排完,此时才可以取出5和7排右子区间,右子区间按相同流程处理即可;
顺序栈与链式栈的实现:顺序栈与链式栈_顺序栈和链栈-CSDN博客
//快排非递归实现
void QuickSortNonR(int* a, int begin, int end)
{
Stack st;
InitStack(&st);
StackPush(&st, end);
StackPush(&st, begin);
while (!StackEmpty(&st))
{
int left = StackTop(&st);
StackPop(&st);
int right = StackTop(&st);
StackPop(&st);
int keyi = PartSort(a, left, right);
//[left keyi-1] keyi [keyi+1 right]
if (right > keyi + 1)
{
StackPush(&st, right);
StackPush(&st, keyi+1);
}
if (keyi - 1 > left)
{
StackPush(&st, keyi - 1);
StackPush(&st, left);
}
}
DestroyStack(&st);
}快速排序特性总结
1. 时间复杂度
因为每次排序都将待排序序列分成两部分,每部分的长度大约为原序列的一半,因此需要进行logn次排序,每次排序的时间复杂度为O(n),所以快速排序的时间复杂度为O(n*logn);
2. 空间复杂度
因为每次排序需要使用递归调用,每次调用需要使用一定的栈空间,所以快速排序的空间复杂度为O(logn);
3. 算法稳定性
快速排序的算法不稳定,这是因为在排序过程中,可能会出现相同元素的相对位置发生变化的情况;当待排序序列中存在多个相同的元素时,快速排序可能会将它们分到不同的子序列中,从而导致它们的相对位置发生变化;
归并排序
归并排序的基本思想:
将待排序的序列分成若干个子序列,每个子序列都是有序的,然后再将这些有序的子序列合并成一个大的有序序列;
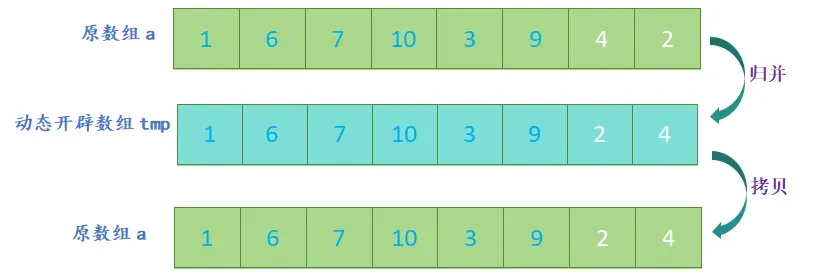
具体实现过程通常采用递归的方法,将序列递归地分成两半,对每一半分别进行归并排序,最后将两个有序的子序列合并成一个有序的序列;在合并的过程中,需要开辟一个数组来存储合并后的序列,然后再将临时数组中的元素拷贝回原数组中;
归并排序的基本思想可以总结为以下三个步骤:
- 分割:将待排序的序列分成若干个子序列,每个子序列都是有序的;
- 合并:将有序的子序列归并到开辟后的数组形成一个大的有序序列;
- 复制:将临时数组中的元素复制回原数组中;

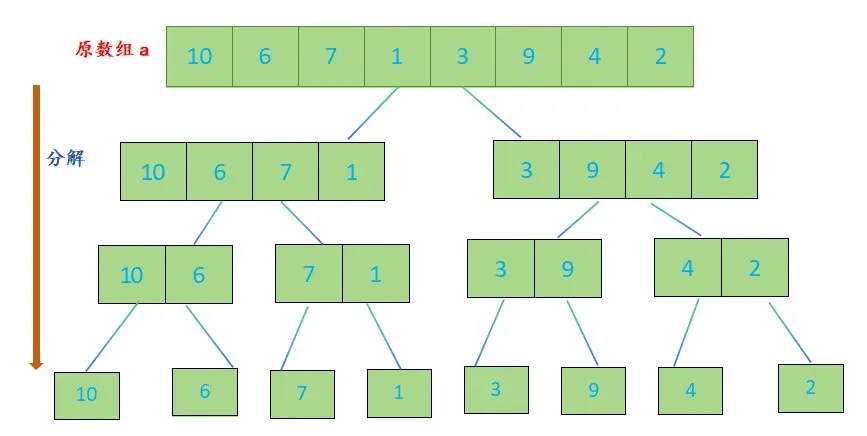
归并排序的实现步骤:
- 分割:将待排序数组从中间位置分成两个子数组,直到每个子数组只有一个元素为止;
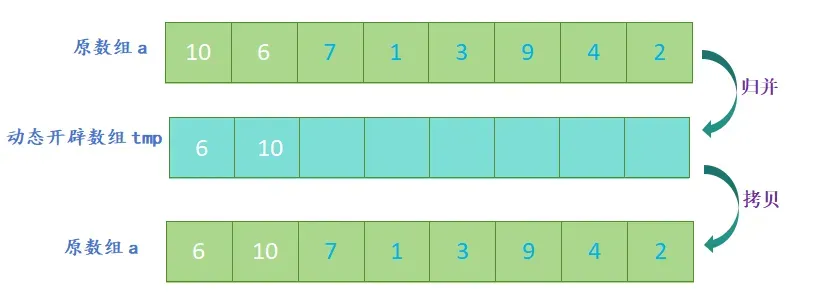
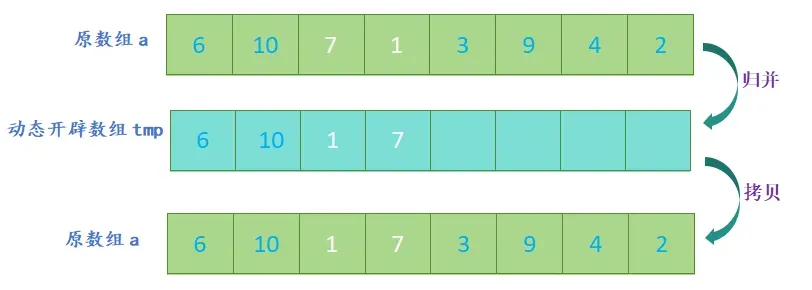
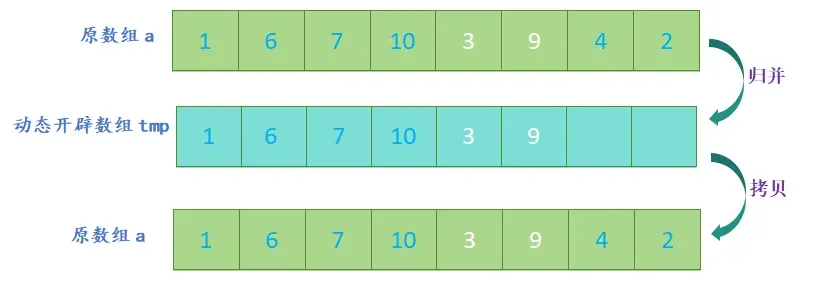
- 归并:将两个有序子数组合并成一个大的有序数组;
- 开辟一个新数组,新数组的大小与原数组大小相同,定义三个指针,分别指向两个子数组和新数组;
- 比较两个子数组的第一个元素,将较小的元素放入新数组中,并将指向该元素的指针向后移动一位;
- 重复上一步,直到其中一个子数组的元素全部放入新数组中;
- 将另一个子数组中剩余的元素依次放入新数组中;



归并排序的代码实现
//归并排序(递归)
//将待排序序列不断二分,直到每个子序列只有一个元素为止,只有一个元素,序列一定有序;
//将相邻的两个子序列合并成一个有序的序列,直到所有子序列都被合并成一个完整的序列;
void SubMergeSort(int* a, int* tmp, int begin, int end)
{
if (begin >= end)
return;
int mid = (begin + end) / 2;
//划分区间为[begin,mid]U[mid+1,end]
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
//递归终止的条件为区间只包含一个元素或者区间不存在;
//后序遍历
SubMergeSort(a, tmp, begin1, end1);
SubMergeSort(a, tmp, begin2, end2);
//首先归并到tmp数组,然后拷贝到原数组;
int index = begin;//tmp数组下标
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
//begin1>end1与begin2>end2至少有一个发生
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//拷贝到原数组
memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
perror("malloc failed");
return;
}
SubMergeSort(a, tmp, 0, n - 1);
}归并排序的特性总结
1. 时间复杂度
归并排序的时间复杂度可以通过递归树来分析;在递归树中,每个节点表示对一个区间进行排序的时间复杂度,而每个节点的子节点表示对该区间的两个子区间进行排序的时间复杂度,因此,递归树的深度为logn,每层的时间复杂度为O(n),因此归并排序的时间复杂度为O(nlogn);
2. 空间复杂度
归并排序的空间复杂度为O(n),因为在排序过程中需要创建一个长度为n的临时数组来存储排序结果;
3. 算法稳定性
归并排序是一种稳定的排序算法,因为在合并两个有序子序列的过程中,如果两个元素相等,那么先出现的元素会先被放入结果数组中,保证了排序的稳定性;
计数排序
计数排序的基本思想:
计数排序不是一个基于比较的排序算法,是记录数据出现次数的一种排序算法;计数排序使用一个额外的count数组,其中第i个元素是待排序数组中值等于i的元素的个数,然后根据count数组来将待排序数组中的元素排到正确的位置;

计数排序的实现步骤:
- 遍历原数组,找出原数组中的最大值max,最小值min;
- 创建count数组,数组大小为max-min+1,并将其元素初始化为0;
- 将原数组里面的值减去原数组最小值min作为count数组的下标映射下来,而count数组里面存放的值就是原数组里面值出现的次数;
- 从前向后依次填充数组,填充数组时,只需要加上这个最小值,就能还原出原来的值;
计数排序的代码实现
//计数排序
void CountSort(int* a, int n)
{
//寻找最大值,最小值
int min = a[0];
int max = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] < min)
min = a[i];
if (a[i]>max)
max = a[i];
}
//确定新数组count的大小
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int)*range);
if (count == NULL)
{
perror("malloc failed:");
return;
}
//新数组全部初始化为0,方便计数
memset(count, 0, sizeof(int)*range);
//统计数据出现的次数
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
//从前向后依次填充原数组
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
free(count);
}计数排序的特性总结
1. 时间复杂度
计数排序的时间复杂度与待排序元素的范围相关,其时间复杂度为O(n+k),其中n为元素数量,k为元素的范围(即最大的元素与最小的元素的差加1);
2. 空间复杂度
计数排序需要额外开辟的空间大小k=max+min-1,所以空间复杂度为O(k);
3. 算法稳定性
计数排序是一个非基于比较的线性时间排序算法,是一种稳定排序;
文章出处登录后可见!
