需求来源
前段时间有个需求要对矩阵数据做归一化处理,之后在对数据做一致性校验,并获取数据对应的权重。
需求分析
1、了解归一化算法
2、通过数据构建矩阵信息
3、数据处理
4、获取权重
实现方案
1、简单说一下概念:
归一化是一种数据处理方式,能将数据经过处理后限制在某个固定范围内。当前的需求是将数据处理为[0,1]之间的小数。
2、计算方法
2.1、归一化算法公式:
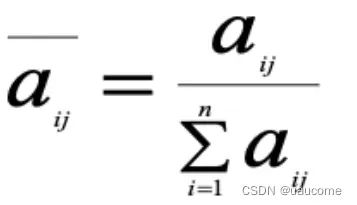
2.2、权重算法公式:
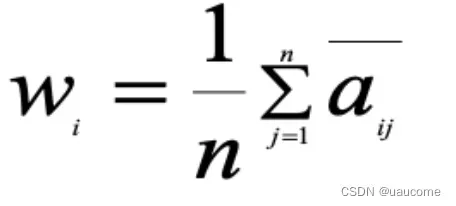
2.3、一致性校验公式:
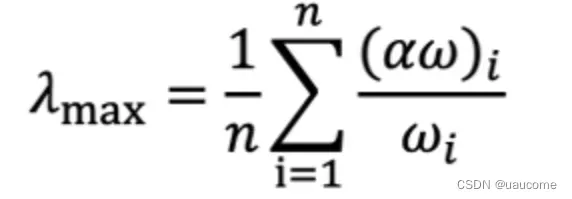
2.4、一致性比例计算:
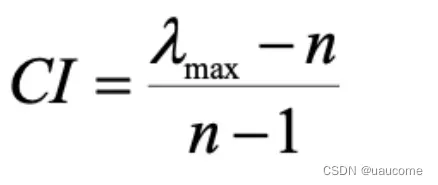
注:当CR<0.1时,具有一致性;否则不具有一致性。
代码实现
代码如下,做个记录:
package com.***.***.**;
import com.alibaba.fastjson.JSON;
import org.apache.commons.lang3.StringUtils;
import org.apache.commons.lang3.math.NumberUtils;
import java.text.DecimalFormat;
import java.util.HashMap;
public class MatrixSet {
/**
* 矩阵横向编码
*/
private static final String MATRIX_X = "X";
/**
* 矩阵纵向编码
*/
private static final String MATRIX_Y = "Y";
/**
* 对应的平均随机一致性指标 RI,目前存放15阶
*/
private static final HashMap<Integer, Double> RI_MAP = new HashMap<>();
private static final DecimalFormat DF = new DecimalFormat("######0.00");
static {
RI_MAP.put(1, 0d);
RI_MAP.put(2, 0d);
RI_MAP.put(3, 0.52d);
RI_MAP.put(4, 0.89d);
RI_MAP.put(5, 1.12d);
RI_MAP.put(6, 1.26d);
RI_MAP.put(7, 1.36d);
RI_MAP.put(8, 1.41d);
RI_MAP.put(9, 1.46d);
RI_MAP.put(10, 1.49d);
RI_MAP.put(11, 1.52d);
RI_MAP.put(12, 1.54d);
RI_MAP.put(13, 1.56d);
RI_MAP.put(14, 1.58d);
RI_MAP.put(15, 1.59d);
}
public static void main(String[] args) {
try {
// 存放权重
HashMap<String, String> weightMap = new HashMap<>();
// 矩阵信息
String matrixData = "[[\"A\",\"1\",\"2\",\"3\"],[\"B\",\"1\",\"5\",\"1/3\"],[\"C\",\"1/5\",\"1\",\"1/7\"],[\"D\",\"3\",\"7\",\"1\"]]";
// 获取矩阵数据
String[][] data = JSON.parseObject(matrixData, String[][].class);
if (data.length > 0) {
// 获取double精度的二维数组
// 原数据数组
double[][] arr = getDoubleArrData(data);
// 数据校验(可对数据做其他逻辑处理)
boolean flag = dataCheck(arr);
// sumColumn值计算
// parameter="X"--横向
// parameter="Y"--纵向
double[] sumColumn = getSumData(arr, "Y");
// 归一化矩阵
double[][] normalizationArr = getNormalizationArrData(arr, sumColumn);
// sumRowColumn值计算
double[] sumRowColumn = getSumData(normalizationArr, "X");
// ω(权重)
double[] weightColumn = getWeightData(sumRowColumn, arr.length);
System.out.println("权重为:" + JSON.toJSON(weightColumn));
// 𝛼ω
double[] aWeightColumn = getAWeightdata(arr, weightColumn);
// λmax = sum(每个𝛼ω/每个ω)
double λmax = getAmax(aWeightColumn, weightColumn);
// CI=(λmax-n)/(n-1)
double ci = (λmax - arr.length) / (arr.length - 1);
// RI
double ri = RI_MAP.get(arr.length);
// CR=CI/RI
double cr = ci / ri;
if (cr >= 0.1) {
System.out.println("当前矩阵不具有一致性");
}
else {
// 存放指标权重
for (int i = 0; i < weightColumn.length; i++) {
// 可根据需要做数据处理
weightMap.put(i + "", DF.format(weightColumn[i]));
}
}
}
else {
System.out.println("当前矩阵值为空");
}
}
catch (Exception e) {
System.out.println("矩阵数据处理异常,consistencyCheck:" + e.getMessage());
}
}
/**
* 获取double精度的二维数组
*
* @param orginArr 原始矩阵数据
* @return 结果
*/
private static double[][] getDoubleArrData(String[][] orginArr) {
double[][] data = new double[orginArr.length - 1][orginArr.length - 1];
for (int i = 1; i < orginArr.length; i++) {
for (int j = 1; j < orginArr.length; j++) {
if (orginArr[i][j].indexOf("/") > 0) {
if (StringUtils.isNotBlank(orginArr[i][j].split("/")[1])
&& NumberUtils.toDouble(orginArr[i][j].split("/")[1]) != 0) {
double newDoubleData = NumberUtils.toDouble(orginArr[i][j].split("/")[0], 0d)
/ NumberUtils.toDouble(orginArr[i][j].split("/")[1]);
data[i - 1][j - 1] = newDoubleData;
}
else {
System.out.println("填写的数据不能为空!");
}
}
else {
data[i - 1][j - 1] = NumberUtils.toDouble(orginArr[i][j]);
}
}
}
return data;
}
/**
* 数据校验
*
* @param arr 原数组
* @return 结果
*/
private static boolean dataCheck(double[][] arr) {
boolean result = false;
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length; j++) {
if (arr[i][j] == 0) {
result = true;
}
}
}
return result;
}
/**
* 获取矩阵每行或者每列数据之和
*
* @param arr 矩阵参数
* @param arr 矩阵参数
* @return 结果
*/
private static double[] getSumData(double[][] arr, String parameter) {
double[] result = new double[arr.length];
for (int i = 0; i < arr.length; i++) {
double column = 0d;
for (int j = 0; j < arr.length; j++) {
if (StringUtils.equals(MATRIX_X, parameter)) {
column += arr[i][j];
}
else if (StringUtils.equals(MATRIX_Y, parameter)) {
column += arr[j][i];
}
}
result[i] = column;
}
return result;
}
/**
* 获取归一化矩阵
*
* @param arr 原数组
* @param sumColumn 原数组纵向之和数组
* @return 结果
*/
private static double[][] getNormalizationArrData(double[][] arr, double[] sumColumn) {
double[][] normalizationArr = new double[arr.length][arr.length];
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length; j++) {
normalizationArr[i][j] = arr[i][j] / sumColumn[j];
}
}
return normalizationArr;
}
/**
* 获取权重数组
*
* @param sumRowColumn
* @param length
* @return
*/
private static double[] getWeightData(double[] sumRowColumn, int length) {
double[] weightColumn = new double[sumRowColumn.length];
for (int i = 0; i < weightColumn.length; i++) {
weightColumn[i] = sumRowColumn[i] / length;
}
return weightColumn;
}
/**
* 获取𝛼ω
*
* @param arr 原数组
* @param weightColumn 权重
* @return 结果
*/
private static double[] getAWeightdata(double[][] arr, double[] weightColumn) {
double[] aWeightColumn = new double[arr.length];
for (int i = 0; i < arr.length; i++) {
double temp = 0d;
for (int j = 0; j < arr.length; j++) {
temp += arr[i][j] * weightColumn[j];
}
aWeightColumn[i] = temp;
}
return aWeightColumn;
}
/**
* 获取λmax
*
* @param aWeightColumn 𝛼ω列表
* @param weightColumn ω列表
* @return 结果
*/
private static double getAmax(double[] aWeightColumn, double[] weightColumn) {
double λmax = 0d;
for (int i = 0; i < weightColumn.length; i++) {
λmax += aWeightColumn[i] / weightColumn[i];
}
return λmax / aWeightColumn.length;
}
}
文章出处登录后可见!
已经登录?立即刷新
