(一)考试题型
题型一:算法应用题(50分)
线性表,栈,队列-> 操作&应用&结果
树的构造,遍历(中序),存储,哈夫曼树,最佳二叉排序树,平衡二叉排序树,
散列(必考)快速查找,函数构造,冲突地址,平均查找长度
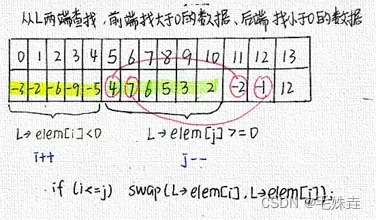
排序算法结果,代码(交换,比较次数,对应过程,复杂度)不考冒泡!
图的存储,遍历,最小生成树,最短路径算法(dite+fulo)考单元
拓扑排序
题型二:算法分析与设计(难度)3道题目,每题15-20分
算法复杂度+算法功能+设计更合理结构+数据结构-核心代码+定义,函数核心代码
(线性表链式,顺式最多考+树结构,功能,输出结果+图结构,图执行结果,遍历,最小生成树,拓扑排序)
(二)核心知识点
考点一:逻辑结构+物理结构+抽象数据类型+算法复杂度
(时间:顺序,选择,循环)


考点二:线性结构
1.线性表定义及其存储实现:顺序表和链接表,优缺点分析(顺序存储可随
机访问,链式存储可灵活利用空间),相关操作的时间复杂度。
2.链表的插入删除操作
3.两种特殊的线性表及其应用:栈、队列
4.栈、队列上的(插入/删除)操作及其特点
5.循环队列满和空的条件
6.能够定义线性表、栈、队列的数据存储结构,能够实现相关操作的算法并
分析时间复杂度(例如插入、删除及其它应用等)
7.理解线性结构的应用( 如根据要求能灵活定义线性表结构,能根据线性表
的插入、删除操作解决实际问题)





考点三:树与二叉树
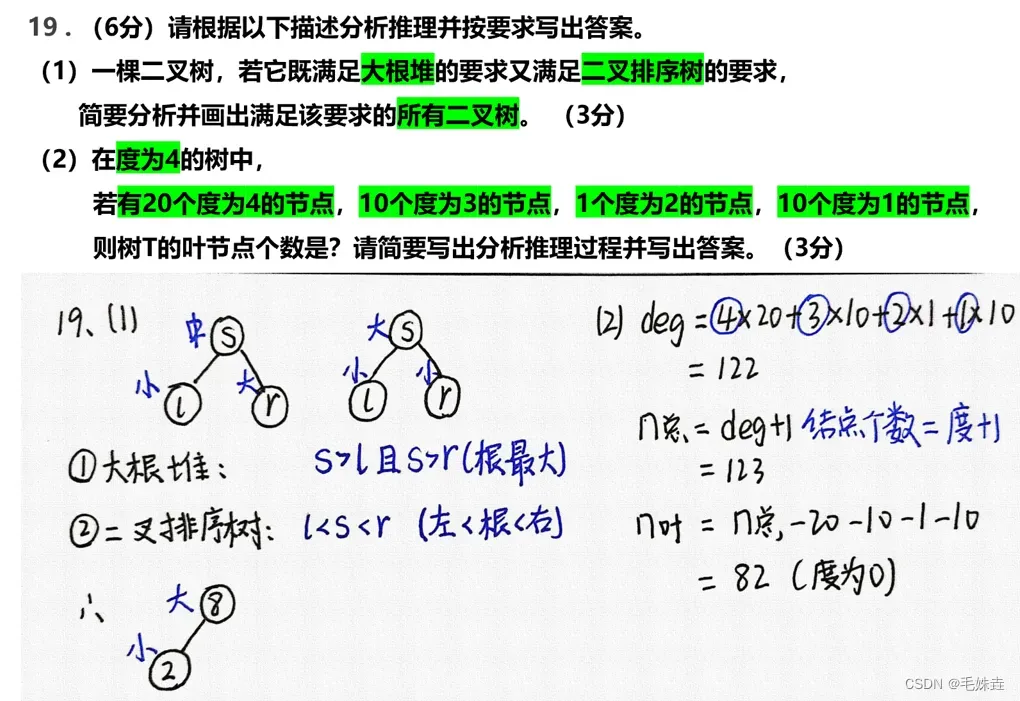
二叉树基本概念与性质(高度、层次、节点的度等)
完全二叉树(堆排序)、满二叉树、扩充二叉树等概念
二叉树的存储结构: (完全二叉树) 顺序存储、二叉链表存储
二叉树的遍历(周游)及算法实现
■给定前(后)序和中序遍历序列,能够构造出二叉树
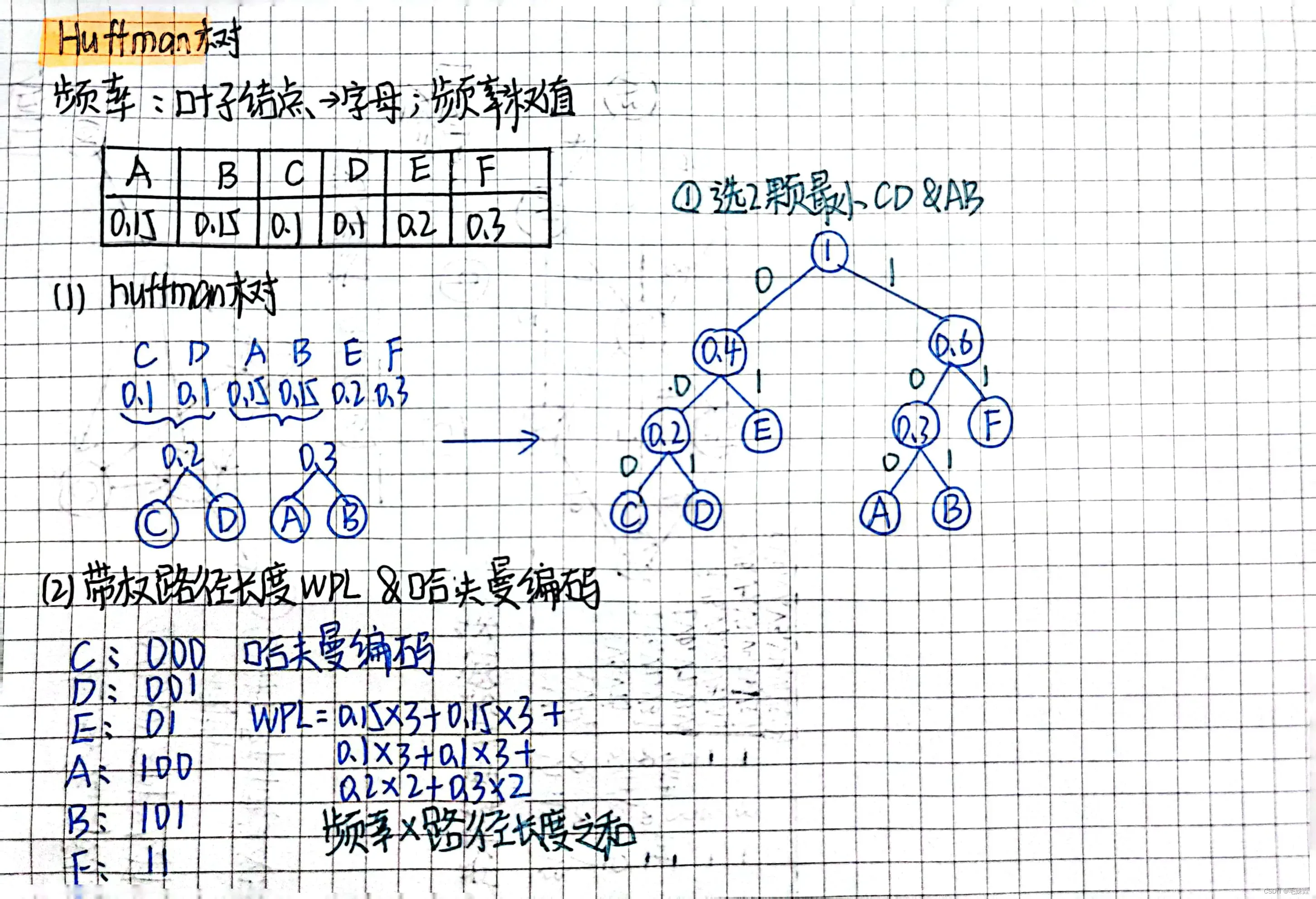
哈夫曼树与哈夫曼编码(前缀编码)、带权路径长度计算
树的存储表示(父指针法、长子兄弟表示法,) ;树、树林与二叉树的等
价转换;
二叉树的递归算法应用:二叉树的创造,遍历,结点的查找,求二叉树的
高度、二叉树的叶子结点数等
考点四:字典与高级字典
1.二分查找算法及其时间复杂度的理解,散列的引入与相关算法
装填因子,散列函数,散列表的长度
2.散列冲突(碰撞、堆积)的解决机制:线性探查法、拉链法
3.散列表构造与(等概率不等概率下的)平均查找长度
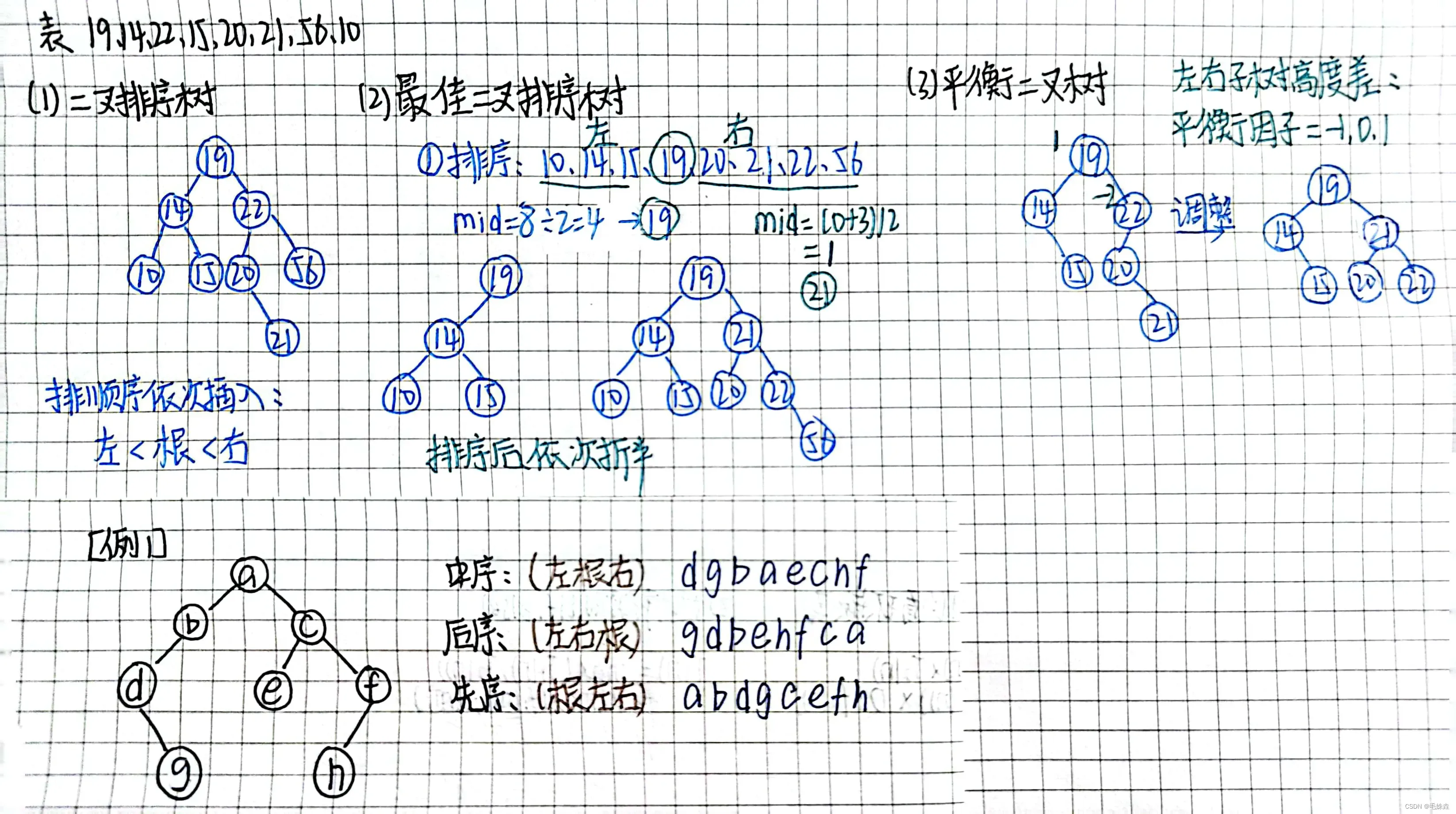
4.二叉排序树的构造、查找和删除方法(构造过程遵照关键字先后次序依次插入),及相应算法实现
5.最佳二叉排序树的构造
6.平衡二叉排序树的概念与调整


考点五:排序
1.排序的策略及代码实现:插入(直接,希尔)、选择(堆排序)、交换(快速排序)、分配、归并
2.直接插入排序、二分法插入 排序、直接选择排序、堆排序、冒泡排序、快速排序、基数排序、二路归并排序(红色为常考)
3.要求能实现并使用各排序算法;能分析各排序算法的优缺点;能基于排序需求选择合适的排序策略
4.排序算法的时间复杂度和空间复杂度及其分析
考点六:图
图的基本概念:连通图、完全图、有向无向、有权无权等
图的存储结构:邻接矩阵与邻接表存储;
图的广度优先遍历和深度优先遍历(图的周游)
最小生成树及其构造: Prim算法、Kruskal算法
单源最短路径:迪杰斯特拉(Dijkstra) 算法
图的拓扑排序等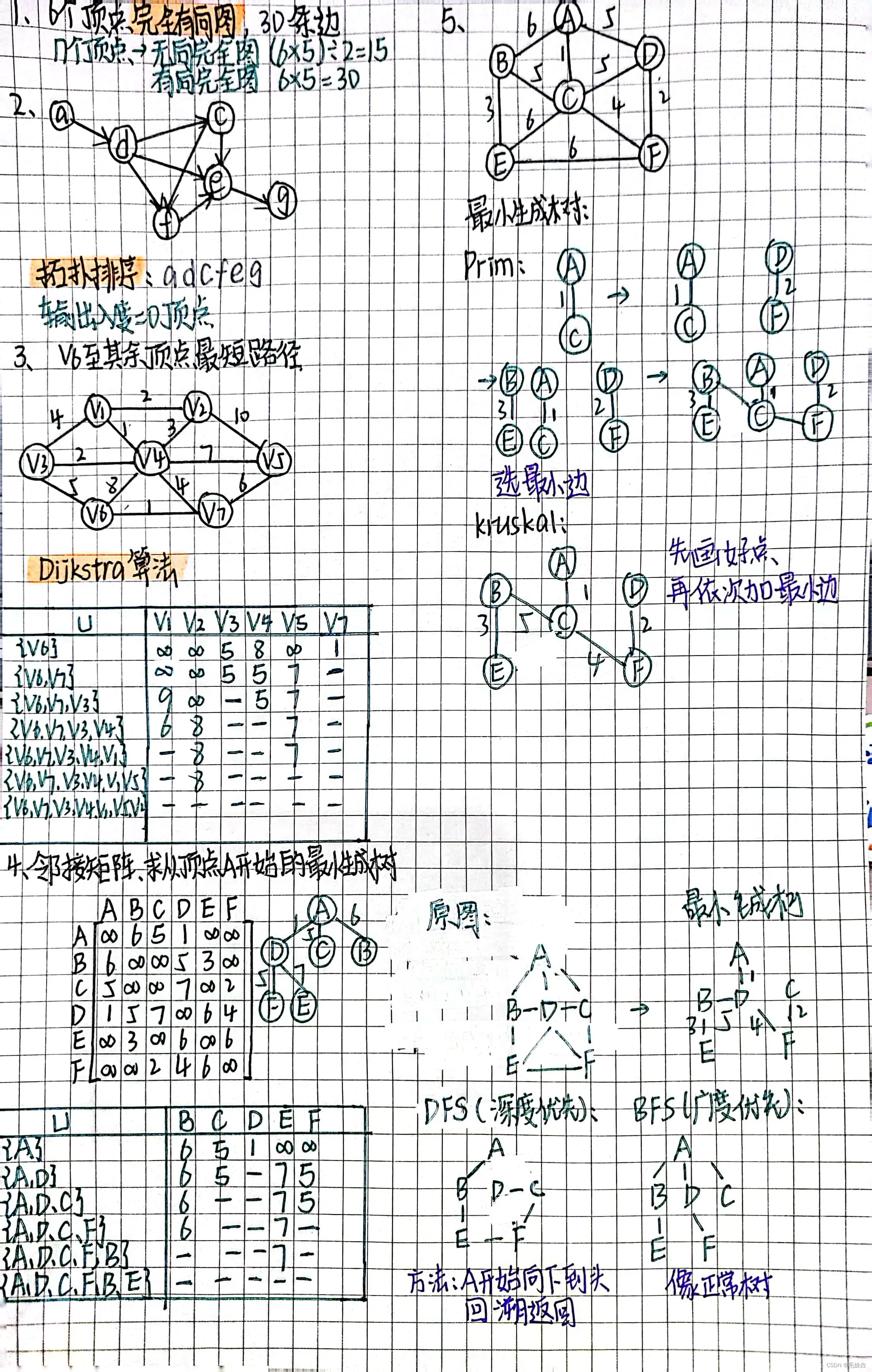
(三)真题试卷
一、应用题(共50分)
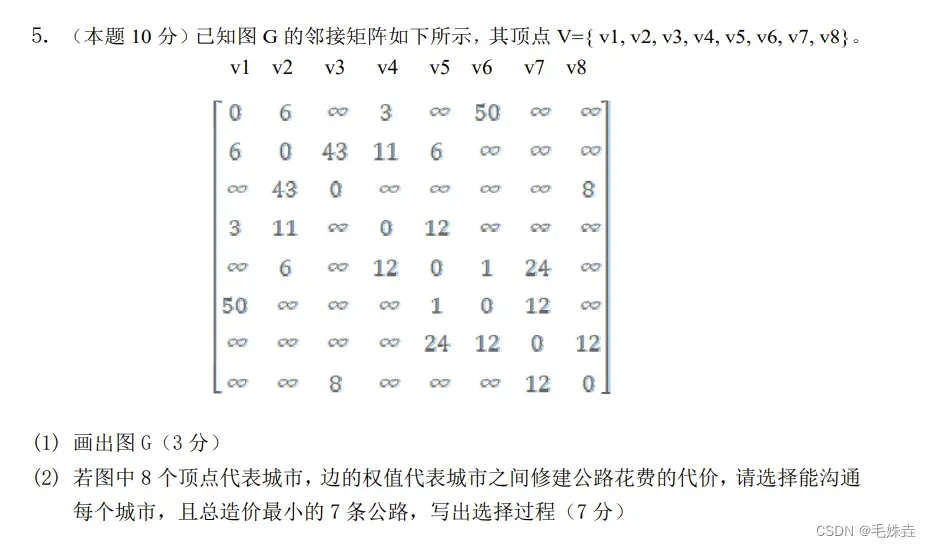
1. (本题10分) – -组记录的关键码为{46, 79, 56, 38, 40, 84, 12},则.
(1) 写出一趟希尔排序后的结果; (3分)
(2)利用快速排序的方法,以第一一个记录为基准,写出一-趟排序后的结果; (3 分)
(3)若使用堆排序,且排序后的关键码要求是递增序,画出初始堆; (4 分)
2. (本题10分)给定一组字符以及它们出现的权值(括号内的值为各字母出现的权值),
D(7), E(31), I(19),L(23),A(11), S(5), V(4)
(1)画出对应的哈夫曼树;(在构造哈夫曼树时要求每棵子树的左孩子的权值不大于右孩子
的权值) (4 分)
(2) 给出每个字符的哈夫曼编码; (4分)
(3)若有编码序列“0001 1001011011101010111”,请依据上面的huffman 树写出译码结
果。(2分)
3. (本题10分)将序列{4, 5, 8,2, 1, 3, 6}中的整数依次插入一棵空的平衡二叉树中,要求依
次画出插入各整数后得到的平衡二叉树。
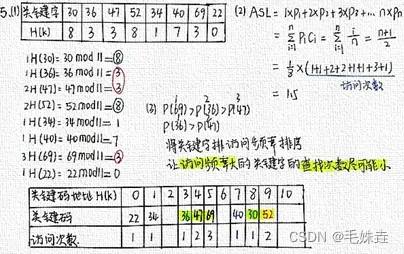
4.将关键字序列{7, 8,30,11, 18, 9,14}散列存储到散列表中。散列函数为: H (key) =
(key*3) %7,处理冲突采用线性探查法,要求负载因子为0.7。
(1) 请画出所构造的散列表; (7分)
(2)分别计算在等概率情况下,查找成功和不成功时的平均查找长度(3 分)。.
二、算法分析及设计题(共50分)



8. (本题12分)给定顺序线性表定义如下:
typedef int DataType;
struct seqList
int MaxNum; //用于记录顺序线性表中能存放的最大元素个数
DataType*Elem;//用于存放顺序线性表数据元素的连续空间的起始地址
int curNum; //线性表中现有元素个数
};
假设一组未排序的整数放在顺序线性表L中,请编写算法找出其中没有出现的最小的正整
数。要求:算法时间复杂度不超过0(n);例如,{-5, 3, 2, 3},未出现的最小正整数是1;
{1, 2,3},未出现的最小正整数是4。
int findMin(struct seqList*L)
{//完成算法,找出L中没有出现的最小的正整数

文章出处登录后可见!