AIGC：使用变分自编码器VAE实现MINIST手写数字生成

1 变分自编码器介绍

变分自编码器（Variational Autoencoders，VAE）是一种生成模型，用于学习数据的分布并生成与输入数据相似的新样本。它是一种自编码器（Autoencoder）的扩展，自编码器是一种用于将输入数据压缩为低维表示并再次解压缩的神经网络结构。VAE的独特之处在于它不仅可以生成新样本，还可以学习数据的概率分布。

VAE的关键思想是将输入数据视为从潜在空间中采样的结果。潜在空间是一个多维空间，每个点都对应着一个可能的数据样本。VAE的目标是学习如何映射输入数据到潜在空间，并从中采样以生成新的样本。

1.1 AE（Autoencoder）

AE（Autoencoder），自动编码器。自编码器的初衷是为了数据降维，假设原始特征x维度过高，那么我们希望通过编码器E将其编码成低维特征向量z=E(x)，编码的原则是尽可能保留原始信息，因此我们再训练一个解码器D，希望能通过z重构原始信息，即x≈D(E(x))，其优化目标一般是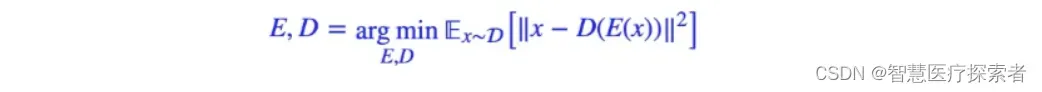

对应的示意图如下：

我们常用的encoder-decoder即为最简单的一种AE。训练过程中加上一些扰动，就可以变成去噪自编码器（DAE）：或者用遮盖（MIM，mask image modeling）的方法来加扰动：

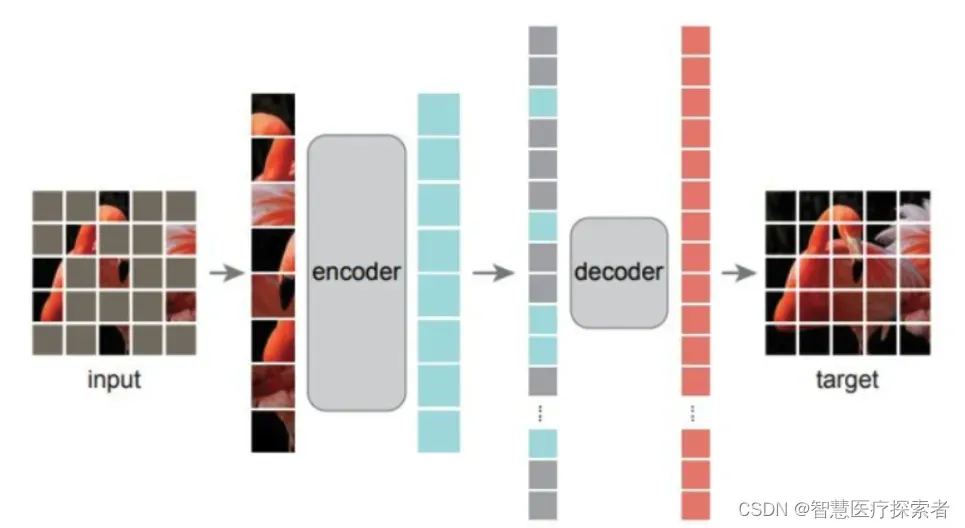
• Encoder：将原始的高维数据映射到低维特征空间，这个特征维度一般比原始数据维度要小，这样就起到压缩或者降维的目的，这个低维特征也往往成为中间隐含特征（latent representation）；

• Decoder：基于压缩后的低维特征来重建原始数据；

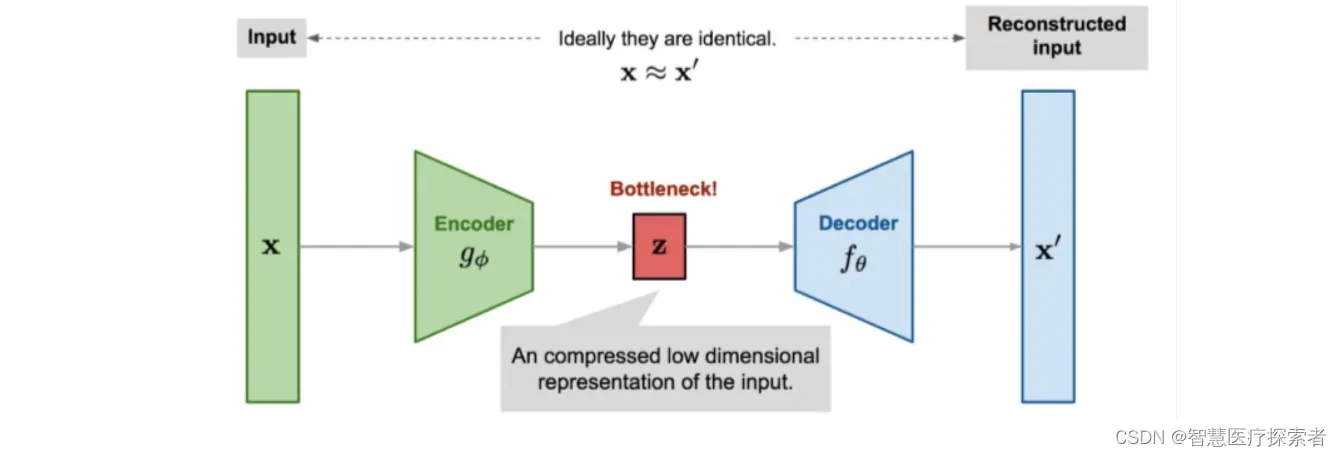
自动编码器是神经网络的一种，其基本思想就是直接使用一层或者多层的神经网络对输入数据进行映射，得到输出向量，作为从输入数据提取出的特征。传统的自动编码器一般用来数据降维或者特征学习，类似于PCA，但是自动编码器比PCA灵活的多，因为它既能表征线性变换又能表征非线性变换。自动编码器可以被看做是前馈网络的一个特例。基本的自编码器模型是一个简单的三层神经网络结构：一个输入层、一个隐藏层和一个输出层。其中输出层和输入层具有相同的维数。

自编码器，它的输入输出是一致的，目标是使用稀疏的高阶特征重新组合来重构自己。自动编码器是一种数据压缩算法，其中数据的压缩和解压缩函数是数据相关的、有损的、从样本中自动学习。

目前自编码器的两个主要用途就是降维、去噪和图像生成。

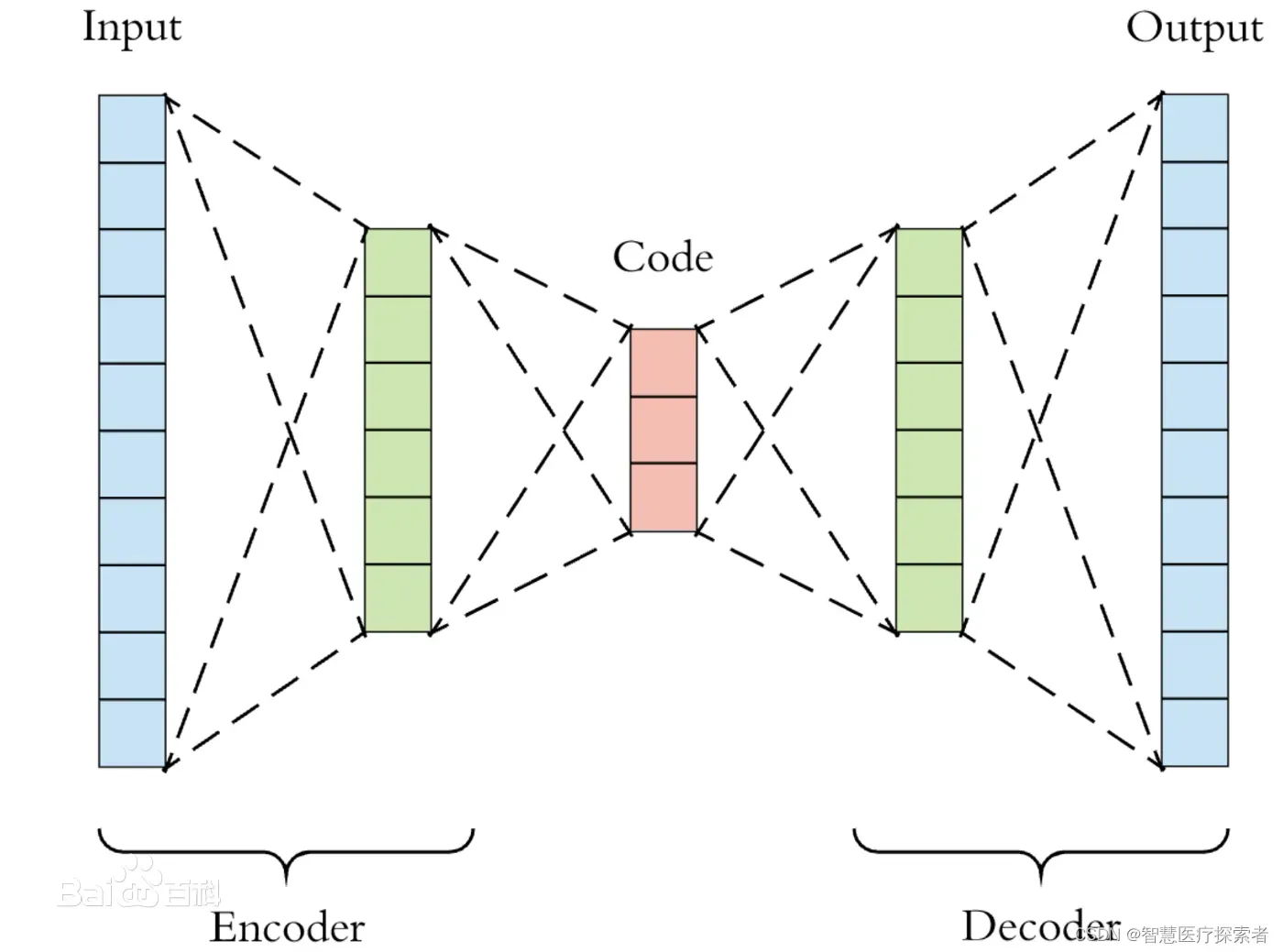
1.2 VAE（Variational Autoencoder）

VAE虽然名字里也带有自动编码器，但这主要是因为VAE和AE有着类似的结构，即encoder和decoder这样的架构设计。实际上，VAE和AE在建模方面存在很大的区别，从本质上讲，VAE是一种基于变分推断（Variational Inference, Variational Bayesian methods）的概率模型（Probabilistic Model），它属于生成模型（当然也是无监督模型）。

• 常拿GAN与VAE进行对比学习，希望构建一个从隐变量Z生成目标数据X的模型，但是实现上有所不同。更准确地讲，它们是假设了Z服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型X=g(Z)，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

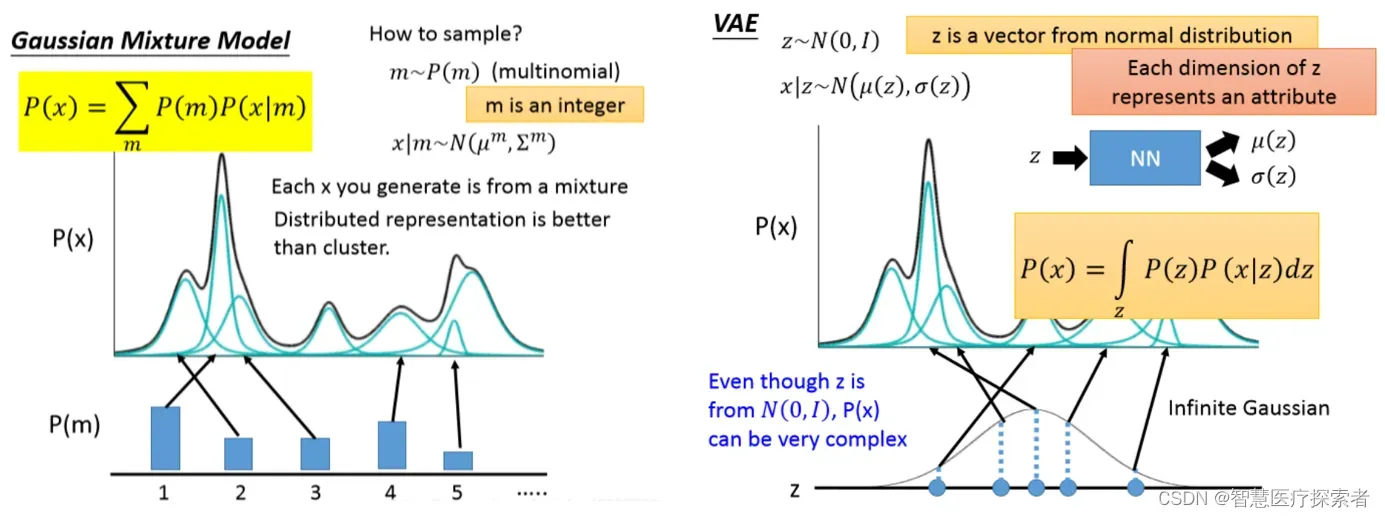
• 首先我们有一批数据样本{X1,…,Xn}，其整体用X来描述，我们本想根据{X1,…,Xn}}得到X的分布p(X)，如果能得到的话，那我直接根据p(X)来采样，就可以得到所有可能的X了（包括{X1,…,Xn}以外的），这是一个终极理想的生成模型了。当然，这个理想很难实现，于是我们将分布改一改，即p(X)=∑Zp(X|Z)p(Z)

• 这里我们就不区分求和还是求积分了，意思对了就行。此时p(X|Z)就描述了一个由Z来生成X的模型，而我们假设Z服从标准正态分布，也就是p(Z)=N(0,I)。如果这个理想能实现，那么我们就可以先从标准正态分布中采样一个Z，然后根据Z来算一个X，也是一个很棒的生成模型。接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现

 那现在假设Z服从标准的正态分布，那么我就可以从中采样得到若干个Z1,Z2,…,Zn，然后对它做变换得到X1=g(Z1),X2=g(Z2),…,Xn=g(Zn)，我们怎么判断这个通过g构造出来的数据集，它的分布跟我们目标的数据集分布是不是一样的呢？

KL散度？？答案是no的，因为此时还仅仅是知道了诺干个样本数据，而KL散度是建立在概率分布公式之上的，所以用不了，这个时候，GAN和VAE就有不同之处了，GAN的思路很直接粗犷：既然没有合适的度量，那我干脆把这个度量也用神经网络训练出来吧！ VAE模型的实现有一种迂回的方式。

1.2.1 VAE模型

其实，在整个VAE模型中，我们并没有去使用p(Z)（隐变量空间的分布）是正态分布的假设，我们用的是假设p(Z|X)（后验分布）是正态分布！！

具体来说，给定一个真实样本X_k，我们假设存在一个专属于X_k的分布p(Z|X_k)（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。为什么要强调“专属”呢？因为我们后面要训练一个生成器X=g(Z)，希望能够把从分布p(Z|X_k)采样出来的一个Z_k还原为X_k。如果假设p(Z)是正态分布，然后从p(Z)中采样一个Z，那么我们怎么知道这个Z对应于哪个真实的X呢？现在p(Z|X_k)专属于X_k，我们有理由说从这个分布采样出来的Z应该要还原到X_k中去。

事实上，在论文《Auto-Encoding Variational Bayes》的应用部分，也特别强调了这一点：

这时候每一个X_k都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个X就有多少个正态分布了。我们知道正态分布有两组参数：均值μ和方差σ^2（多元的话，它们都是向量），接下来我们要找出专属于X_k的正态分布p(Z|X_k)的均值和方差，参考WGAN对于GAN的处理。

让我们来思考一下，根据上图的训练过程，最终会得到什么结果。

首先，我们希望重构X，也就是最小化均方，但是这个重构过程受到噪声的影响，因为Z_k是通过重新采样过的，不是直接encoder算出来的，显然噪声会增加重构的难度，不过好在这个噪声强度（方差）是通过一个神经网络算出来的，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个更容易，而均值是通过另一个神经网络算出来的。

说白了，模型会慢慢退化成普通的AutoEncoder，噪声不再起作用。

vae可以使所有的p（Z|X）都向标准正太分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。如果所有的p（Z|X)都很接近标准正太分布N（0，I），根据定义

这样我们就能达到我们的先验假设：P（Z）是标准正太分布，然后放心的从N（0，I）中采样来生成图像。

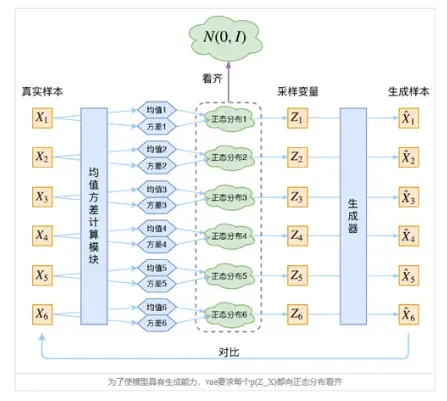
VAE的迂回处理方案：(魅力所在)

• 在整个VAE模型中，我们并没有去使用p(Z)（隐变量空间的分布）是正态分布的假设，我们用的是假设p(Z|X)（后验分布）是正态分布！！

• 具体来说，给定一个真实样本Xk，我们假设存在一个专属于Xk的分布p(Z|Xk)（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。为什么要强调“专属”呢？因为我们后面要训练一个生成器X=g(Z)，希望能够把从分布p(Z|Xk)采样出来的一个Zk还原为Xk。如果假设p(Z)是正态分布，然后从p(Z)中采样一个Z，那么我们怎么知道这个Z对应于哪个真实的X呢？现在p(Z|Xk)专属于Xk，我们有理由说从这个分布采样出来的Z应该要还原到Xk中去。

• 根据专属Xk数据的正态分布p(Z|Xk)，更便于后期生成器的复原，就对于正态分布而言，会有两组参数：均值μ和方差σ2（多元的话，它们都是向量），那如何把他们算出来呢？？这里便引入神经网络进行拟合：这可能就是神经网络的魅力叭。

• 至此，我们便可以构建相对应的两个神经网络μk=f1(Xk),logσ2k=f2(Xk)，这里有一个运算处理细节，取对数操作，是因为σ2k总是非负的，需要加激活函数处理，而拟合logσ2k不需要加激活函数，因为它可正可负。知道了分布之后，便可以从这个专属的正态分布中进行采样一个相应的Zk出来，然后通过相应的生成器可得到Xk=g(Zk) ，然后再进行损失函数计算。（这个损失函数也有一定说法）

为了防止模型会慢慢退化成普通的AutoEncoder，噪声不再起作用。

• VAE还让所有的p(Z|X)都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。怎么理解“保证了生成能力”呢？如果所有的p(Z|X)都很接近标准正态分布N(0,I)，那么根据定义

• 这样我们就能达到我们的先验假设：p(Z)是标准正态分布。然后我们就可以放心地从N(0,I)中采样来生成图像了。

那怎么让所有的p(Z|X)都向N(0,I)看齐呢？

最直接的办法就是重构误差的基础上加入额外的loss！！

• 再进一步，就会面临这二者损失的占比问题，因为占比若未处理好，会导致所生成的图像模糊，。所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的KL散度KL(N(μ,σ2)∥N(0,I))作为这个额外的loss(这里就是避免了比例问题，直接算他们直接的距离作为损失)，计算结果为

1.2.2 推导

由于我们考虑的是各分量独立的多元正态分布，因此只需要推导一元正态分布的情形即可，根据定义：

重参数技巧

实现模型的一个技巧，英文名是reparameterization trick，我这里叫它做重参数吧。其实很简单，就是我们要从p(Z|Xk)中采样一个Zk出来，尽管我们知道了p(Z|Xk)是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的。我们利用

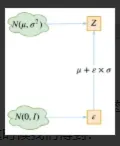
即就是利用该采样的结果进行逆运算优化模型。

上述公式即说明了：(z−μ)/σ=ε是服从均值为0、方差为1的标准正态分布的，要同时把dz考虑进去，是因为乘上dz才算是概率，去掉dz是概率密度而不是概率。这时候我们得到： 从N(μ,σ2)中采样一个Z，相当于从N(0,I)中采样一个ε，然后让Z=μ+ε×σ。

对于变分理论理解：

变分推导 vae训练流程：

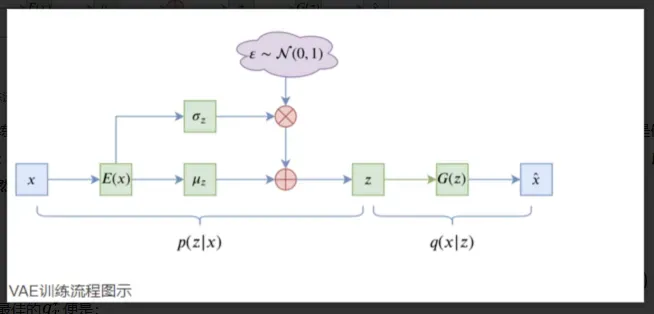
• 训练数据即为观测变量， 假设它由不能直接观测到的潜变量x生成， 于是，生成观测变量过程便是似然分布：p(X|Z)，也就是解码器，因而编码器自然就是后验分布:p(X|Z).根据贝叶斯公式,建立先验、后验和似然的关系:

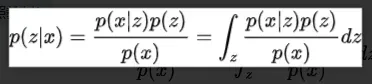
接下来，基于上面变分推断的思想，我们假设变分分布q_x(z), 通过最小化KL散度来近似后验分布p(z|x)，于是，最佳的q^*_x便是：

因为训练数据 x是确定的，因此 log p(x)是一个常数，于是上面的优化问题等价于：

这里的推导：一个简单的对数转化以及一个KL散度近似问题

此时，观察一下优化方程的形式…已经是我们前面所说的VAE的损失函数了

显然，跟我们希望解码准确的目标是一致的。要解码的准，则p(X|Z)应该尽可能的小，编码特征z的分布 q_x(z)同p(z)尽可能的接近，此时恰好-log p(x|z)和 KL(q_x(z)||p(z)) 都尽可能的小，与损失的优化的目标也一致。

1.2.3 极值处理

• VAE的潜变量分布p(z)应该能满足海量的输入数据x并且相互独立，基于中心极限定理，以及为了方便采样，我们有理由直接假设p(z) 是一个标准的高斯分布N(0,1)。 编码解码在编码部分中：

• 就是希望拟合分布尽可能接近p(z)=N(0,1)， 关键就在于基于输入x计算μ和 σ, 直接算有点困难，于是就使用两个神经网络f(x)和g(x) 来无脑拟合 μ和σ 。

• 值得一提的是，很多地方实际使用的f(x)、g(x)两部分神经网络并不是独立的，而是有一部分交集，即他们都先通过一个 h(x)映射到一个中间层h, 然后分别对h计算 f(x)和h(x) . 这样错的好处的话一方面是可以减少参数数量，另外这样算应该会导致拟合的效果差一些，算是防止过拟合吧。

在解码部分中：

解码，即从潜变量z生成数据x的过程，在于最大化似然p(x|z) ，那这应该是个什么分布呢？通常我们假设它是一个伯努利分布或是高斯分布。 分布类型知道之后，那计算-log p(x|z) 最小值其实只要把分布公式带进去算就ok了

其他：

1.2.4 本质分析

VAE虽然也称是AE（AutoEncoder）的一种，但它的做法（或者说它对网络的诠释）是别具一格的。在VAE中，它的Encoder有两个，一个用来计算均值，一个用来计算方差，这已经让人意外了：Encoder不是用来Encode的，是用来算均值和方差的，这真是大新闻了，还有均值和方差不都是统计量吗，怎么是用神经网络来算的？

事实上，我觉得VAE从让普通人望而生畏的变分和贝叶斯理论出发，最后落地到一个具体的模型中，虽然走了比较长的一段路，但最终的模型其实是很接地气的：它本质上就是在我们常规的自编码器的基础上，对encoder的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果decoder能够对噪声有鲁棒性；而那个额外的KL loss（目的是让均值为0，方差为1），事实上就是相当于对encoder的一个正则项，希望encoder出来的东西均有零均值。

那另外一个encoder（对应着计算方差的网络）的作用呢？它是用来动态调节噪声的强度的。直觉上来想，当decoder还没有训练好时（重构误差远大于KL loss），就会适当降低噪声（KL loss增加），使得拟合起来容易一些（重构误差开始下降）；反之，如果decoder训练得还不错时（重构误差小于KL loss），这时候噪声就会增加（KL loss减少），使得拟合更加困难了（重构误差又开始增加），这时候decoder就要想办法提高它的生成能力了。

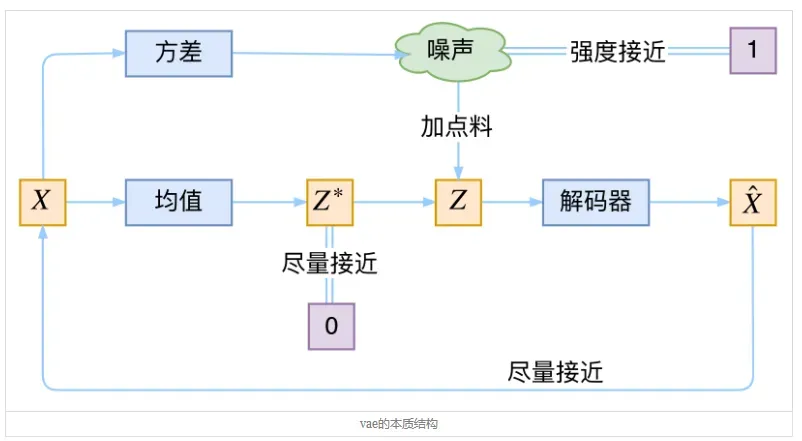
说白了，重构的过程是希望没噪声的，而KL loss则希望有高斯噪声的，两者是对立的。所以，VAE跟GAN一样，内部其实是包含了一个对抗的过程，只不过它们两者是混合起来，共同进化的。从这个角度看，VAE的思想似乎还高明一些，因为在GAN中，造假者在进化时，鉴别者是安然不动的，反之亦然。当然，这只是一个侧面，不能说明VAE就比GAN好。

1.2 工作原理

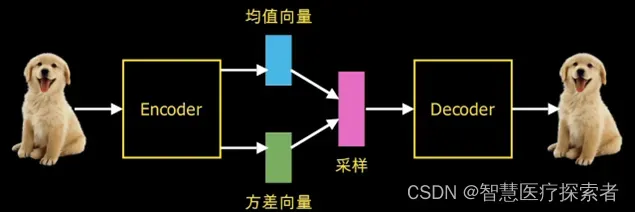
1.2.1 编码器（Encoder）

VAE的第一部分是编码器，它接受输入数据并将其映射到潜在空间中的一个点。编码器的任务是学习如何将数据压缩为潜在空间中的低维表示。

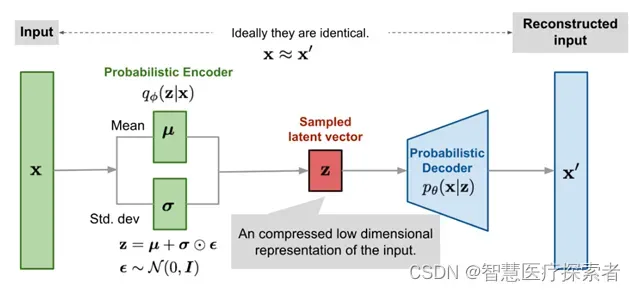
编码器通常由一个神经网络组成，它将输入数据转换为潜在空间中的均值（mean）和方差（variance）参数。这些参数用于定义潜在空间中的概率分布。

1.2.2 采样（Sampling）

一旦我们有了潜在空间中的均值和方差参数，我们可以从这个分布中采样得到一个点。这个采样过程是VAE的关键之一，它使我们能够生成新的样本。

1.2.3 解码器（Decoder）

采样得到的点被送入解码器，解码器的任务是将潜在空间中的点映射回原始数据空间，从而生成新的样本。解码器通常也由一个神经网络组成。

解码器生成的样本与原始输入数据相似，但不完全相同。这种差异使VAE能够生成多样化的样本。

1.2.4 损失函数（Loss Function）

VAE的损失函数由两部分组成：

• 重构损失（Reconstruction Loss）：度量生成样本与原始输入数据之间的差异。它鼓励解码器生成与原始数据相似的样本。

• KL散度（KL Divergence）：度量潜在空间中的分布与标准正态分布之间的差异。它鼓励潜在空间中的点分布在一个标准正态分布附近，从而使采样过程更加有效。

VAE的目标是最小化总损失，以便同时生成与原始数据相似的样本并学习潜在空间的分布。

1.3 应用

1.3.1 图像生成

VAE可以用于生成逼真的图像，如人脸、风景等。它可以用于艺术创作、电影特效和虚拟现实等领域。

1.3.2 图像修复

VAE可以用于修复损坏的图像，从而提高图像质量。这在医学图像处理、老照片修复和图像增强中非常有用。

1.3.3 文本生成

VAE可以用于生成自然语言文本，如文章、故事或对话。这在自然语言处理、文本生成和聊天机器人开发中有广泛的应用。

1.3.4 数据压缩

VAE可以用于数据压缩，将大量数据压缩为更小的表示形式，从而节省存储空间。这在数据传输和存储中非常有用。

2 使用VAE实现MINIST手写数字图片生成

2.1 数据准备与加载

# 创建数据加载器
transform = transforms.Compose([transforms.ToTensor()])
train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)

2.2 构造VAE网络

class Encoder(nn.Module):
    def __init__(self, input_dim, hidden_dim, latent_dim):
        super(Encoder, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc_mu = nn.Linear(hidden_dim, latent_dim)
        self.fc_logvar = nn.Linear(hidden_dim, latent_dim)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        mu = self.fc_mu(x)
        logvar = self.fc_logvar(x)
        return mu, logvar


class Decoder(nn.Module):
    def __init__(self, latent_dim, hidden_dim, output_dim):
        super(Decoder, self).__init__()
        self.fc1 = nn.Linear(latent_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, z):
        z = torch.relu(self.fc1(z))
        x_hat = torch.sigmoid(self.fc2(z))
        return x_hat


class VAE(nn.Module):
    def __init__(self, encoder, decoder):
        super(VAE, self).__init__()
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, x):
        mu, logvar = self.encoder(x)
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        z = mu + eps * std
        x_hat = self.decoder(z)
        return x_hat, mu, logvar

2.3 定义损失函数

def vae_loss_f(x_hat, x, mu, log_var):
    """
    Calculate the loss. Note that the loss includes two parts.
    :return: total loss, BCE and KLD of our model
    """
    # 1. the reconstruction loss.
    # We regard the MNIST as binary classification
    BCE = F.binary_cross_entropy(x_hat, x, reduction='sum')

    # 2. KL-divergence
    KLD = 0.5 * torch.sum(torch.exp(log_var) + torch.pow(mu, 2) - 1. - log_var)

    # 3. total loss
    loss = BCE + KLD
    return loss, BCE, KLD

2.4 模型训练

def train_vae(model, dataloader, optimizer, criterion, device):
    model.train()
    running_loss = 0.0
    for batch_index, (x, _) in enumerate(dataloader):
        x = x.to(device)
        optimizer.zero_grad()
        recon_batch, mu, logvar = model(x.view(-1, 784))
        loss, _, _ = criterion(recon_batch, x.view(-1, 784), mu, logvar)
        loss.backward()
        running_loss += loss.item()
        optimizer.step()
    return running_loss / len(dataloader.dataset)

# 定义超参数
input_dim = 784
hidden_dim = 256
latent_dim = 20
output_dim = 784
batch_size = 128
epochs = 20
save_dir = './result/checkpoint'
result_dir = './result/image'

# 创建数据加载器
transform = transforms.Compose([transforms.ToTensor()])
train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)

# 创建VAE模型
encoder = Encoder(input_dim, hidden_dim, latent_dim)
decoder = Decoder(latent_dim, hidden_dim, output_dim)
vae = VAE(encoder, decoder)

# 定义优化器和损失函数
optimizer = optim.Adam(vae.parameters(), lr=0.001)
criterion = vae_loss_f

# 训练VAE模型
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
vae.to(device)
for epoch in range(epochs):
    train_loss = train_vae(vae, train_loader, optimizer, criterion, device)
    print(f"Epoch {epoch+1}/{epochs}, Loss: {train_loss:.4f}")

2.5 完整代码

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torch.nn.functional as F
from torchvision.utils import save_image
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import os
import shutil


class Encoder(nn.Module):
    def __init__(self, input_dim, hidden_dim, latent_dim):
        super(Encoder, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc_mu = nn.Linear(hidden_dim, latent_dim)
        self.fc_logvar = nn.Linear(hidden_dim, latent_dim)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        mu = self.fc_mu(x)
        logvar = self.fc_logvar(x)
        return mu, logvar


class Decoder(nn.Module):
    def __init__(self, latent_dim, hidden_dim, output_dim):
        super(Decoder, self).__init__()
        self.fc1 = nn.Linear(latent_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, z):
        z = torch.relu(self.fc1(z))
        x_hat = torch.sigmoid(self.fc2(z))
        return x_hat


class VAE(nn.Module):
    def __init__(self, encoder, decoder):
        super(VAE, self).__init__()
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, x):
        mu, logvar = self.encoder(x)
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        z = mu + eps * std
        x_hat = self.decoder(z)
        return x_hat, mu, logvar


def vae_loss_f(x_hat, x, mu, log_var):
    """
    Calculate the loss. Note that the loss includes two parts.
    :return: total loss, BCE and KLD of our model
    """
    # 1. the reconstruction loss.
    # We regard the MNIST as binary classification
    BCE = F.binary_cross_entropy(x_hat, x, reduction='sum')

    # 2. KL-divergence
    KLD = 0.5 * torch.sum(torch.exp(log_var) + torch.pow(mu, 2) - 1. - log_var)

    # 3. total loss
    loss = BCE + KLD
    return loss, BCE, KLD


def train_vae(model, dataloader, optimizer, criterion, device):
    model.train()
    running_loss = 0.0
    for batch_index, (x, _) in enumerate(dataloader):
        x = x.to(device)
        optimizer.zero_grad()
        recon_batch, mu, logvar = model(x.view(-1, 784))
        loss, _, _ = criterion(recon_batch, x.view(-1, 784), mu, logvar)
        loss.backward()
        running_loss += loss.item()
        optimizer.step()
    return running_loss / len(dataloader.dataset)


def test_vae(model, optimizer, mnist_test, epoch, best_test_loss):
    test_avg_loss = 0.0
    with torch.no_grad():  # 这一部分不计算梯度，也就是不放入计算图中去
        '''测试测试集中的数据'''
        # 计算所有batch的损失函数的和
        for test_batch_index, (test_x, _) in enumerate(mnist_test):
            test_x = test_x.to(device)
            # 前向传播
            test_x_hat, test_mu, test_log_var = model(test_x)
            # 损害函数值
            test_loss, test_BCE, test_KLD = vae_loss_f(test_x_hat, test_x, test_mu, test_log_var)
            test_avg_loss += test_loss

        # 对和求平均，得到每一张图片的平均损失
        test_avg_loss /= len(mnist_test.dataset)

        '''测试随机生成的隐变量'''
        # 随机从隐变量的分布中取隐变量
        z = torch.randn(batch_size, latent_dim).to(device)  # 每一行是一个隐变量，总共有batch_size行
        # 对隐变量重构
        random_res = model.decode(z).view(-1, 1, 28, 28)
        # 保存重构结果
        save_image(random_res, './%s/random_sampled-%d.png' % (result_dir, epoch + 1))

        '''保存目前训练好的模型'''
        # 保存模型
        is_best = test_avg_loss < best_test_loss
        best_test_loss = min(test_avg_loss, best_test_loss)
        save_checkpoint({
            'epoch': epoch,  # 迭代次数
            'best_test_loss': best_test_loss,  # 目前最佳的损失函数值
            'state_dict': model.state_dict(),  # 当前训练过的模型的参数
            'optimizer': optimizer.state_dict(),
        }, is_best, save_dir)

        return best_test_loss


def save_checkpoint(state, is_best, outdir):
    """
    每训练一定的epochs后， 判断损失函数是否是目前最优的，并保存模型的参数
    """
    if not os.path.exists(outdir):
        os.makedirs(outdir)

    checkpoint_file = os.path.join(outdir, 'checkpoint.pth')
    best_file = os.path.join(outdir, 'model_best.pth')
    # 把state保存在checkpoint_file文件夹中
    torch.save(state, checkpoint_file)
    if is_best:
        shutil.copyfile(checkpoint_file, best_file)


# 定义超参数
input_dim = 784
hidden_dim = 256
latent_dim = 20
output_dim = 784
batch_size = 128
epochs = 20
save_dir = './result/checkpoint'
result_dir = './result/image'

# 创建数据加载器
transform = transforms.Compose([transforms.ToTensor()])
train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)

# 创建VAE模型
encoder = Encoder(input_dim, hidden_dim, latent_dim)
decoder = Decoder(latent_dim, hidden_dim, output_dim)
vae = VAE(encoder, decoder)

# 定义优化器和损失函数
optimizer = optim.Adam(vae.parameters(), lr=0.001)
criterion = vae_loss_f

# 训练VAE模型
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
vae.to(device)
for epoch in range(epochs):
    train_loss = train_vae(vae, train_loader, optimizer, criterion, device)
    print(f"Epoch {epoch+1}/{epochs}, Loss: {train_loss:.4f}")

# 生成手写数字图像
with torch.no_grad():
    z = torch.randn(64, latent_dim).to(device)
    generated_images = vae.decoder(z).view(-1, 1, 28, 28).cpu()

# 显示生成的图像
fig, axes = plt.subplots(8, 8, figsize=(10, 10))
for i, ax in enumerate(axes.flatten()):
    ax.imshow(generated_images[i][0], cmap='gray')
    ax.axis('off')
plt.show()

运行代码显示：

Epoch 1/20, Loss: 173.6210
Epoch 2/20, Loss: 127.4101
Epoch 3/20, Loss: 118.5472
Epoch 4/20, Loss: 114.7103
Epoch 5/20, Loss: 112.5785
Epoch 6/20, Loss: 111.1329
Epoch 7/20, Loss: 110.1246
Epoch 8/20, Loss: 109.2917
Epoch 9/20, Loss: 108.6825
Epoch 10/20, Loss: 108.1672
Epoch 11/20, Loss: 107.6647
Epoch 12/20, Loss: 107.3654
Epoch 13/20, Loss: 106.9989
Epoch 14/20, Loss: 106.7424
Epoch 15/20, Loss: 106.5040
Epoch 16/20, Loss: 106.2575
Epoch 17/20, Loss: 106.0131
Epoch 18/20, Loss: 105.8500
Epoch 19/20, Loss: 105.7063
Epoch 20/20, Loss: 105.5470

3 总结

变分自编码器（VAE）是一种强大的生成模型，可用于生成图像、文本和音频等各种数据类型。本文介绍了VAE的原理，并提供了一个使用PyTorch的示例来生成手写数字图像。