目录
注
本笔记参考《数据结构(C语言版)(第2版)》
图是一种比线性表和树更复杂是数据结构。在线性表中,数据元素之间存在线性关系;在树形结构中,数据元素之间存在层次关系。但是,到了图结构中,结点之间的关系可以是任意的,这意味着任意两个数据元素都可能相关。
图的定义
||| 图(Graph,记为G)由两个集合V和E组成,记为G(V, E)。其中:
- V(顶点):顶点的有穷非空集合(V(G)表示图G的顶点集合);
- E(边):V中顶点偶对的有穷集合,偶对称的顶点连成了边(E(G)表示图G的边集合,可以为空。为空时,图G只有顶点) 。
| 有向图 | 无向图 | |
| 使用的括号 | < > | ( ) |
| 方向 | <x, y> 表示从顶点x到顶点y的一条有向边 | 无特定方向 |
| 边的区别 | <x, y> 和 <y, x> 是不同的两条边 | (x, y) 和 (y, x) 是同一条边 |
对于有向图而言,<x, y> 也可以被称为一条弧。其中,x为弧尾,y为弧头。
【例子】
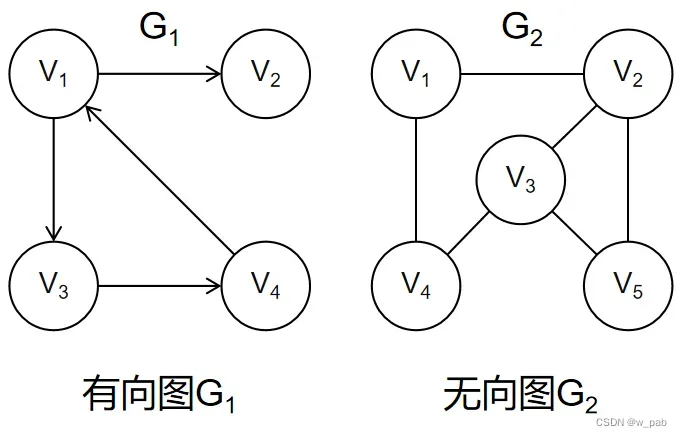
图的基本术语
用n表示图中的顶点,用e表示边的数目,图有如下的基本术语:
| 名称 | 解释 |
| 子图 |
设图G = (V, E),图G’ = (V’, E’): 若V’ ⊆ V,且E’ ⊆ E,则G’是G的子图。 |
| 无向完全图和有向完全图 |
• 无向完全图:①是无向图;②具有n(n-1)/2条边。 • 有向完全图:①是有向图;②具有n(n-1)条弧。 |
| 稀疏图和稠密图 |
• 稀疏图:边/弧很少的图(譬如e<nlog₂n)。 • 稠密图:边/弧很多的图。 |
| 权和网 |
• 权:每条边上具有的,有某种含义的数值。 • 网:带权的图被称为网。 |
| 邻接点 | 两个结点由一条无向边或者有向边关联,则称这两个结点为邻接点。 |
| 度、入度和出度 |
• 顶点v的度:和v关联的边的数目,记为TD(v)。 • 对于有向图,顶点的度分为入度和出度: 入度:以顶点为头的弧的数目,记为ID(v); 出度:以顶点为尾的弧的数目,记为OD(v)。 有公式:TD(v) = ID(v) + OD(v) |
| 路径和路径长度 |
• 路径:是由 顶点v 到 顶点v’ 的一个顶点序列(若G是有向图,则路径也是有向的)。 • 路径长度:是一条路径上的边/弧的数目。 |
| 回路(或称 环 ) | 是第一个顶点和最后一个顶点相同的路径。 |
|
简单路径、 简单回路(或称 简单环 ) |
• 简单路径:序列中顶点不重复出现的路径。 • 简单回路/简单环:除第一个顶点和最后一个顶点外,其余顶点不重复的回路。 |
| 连通、连通图和连通分量 |
• 连通:从 顶点v 到顶点v’ 有路径,则称v和v’是连通的。 • 连通图:若图G中任意两个顶点连通,则图G是连通图(例:上图的G₂)。 • 连通分量:即无向图中的极大连通子图。 |
| 强连通图和强连通分量 |
• 强连通图:在有向图G中,若对于每一对 v 和 v’ ∈ V(v ≠ v’),从 v 到v’ 和从 v’ 到 v 都有路径,则图G是强连通图。 • 强连通分量:有向图中的极大连通子图被称为有向图的强连通分量。 |
||| 连通图的生成树:
- 是一个极小连通子图(含有图中的所有顶点,是边最少的连通子图);
- 只有足以构成一棵树的n – 1条边。
【例子】
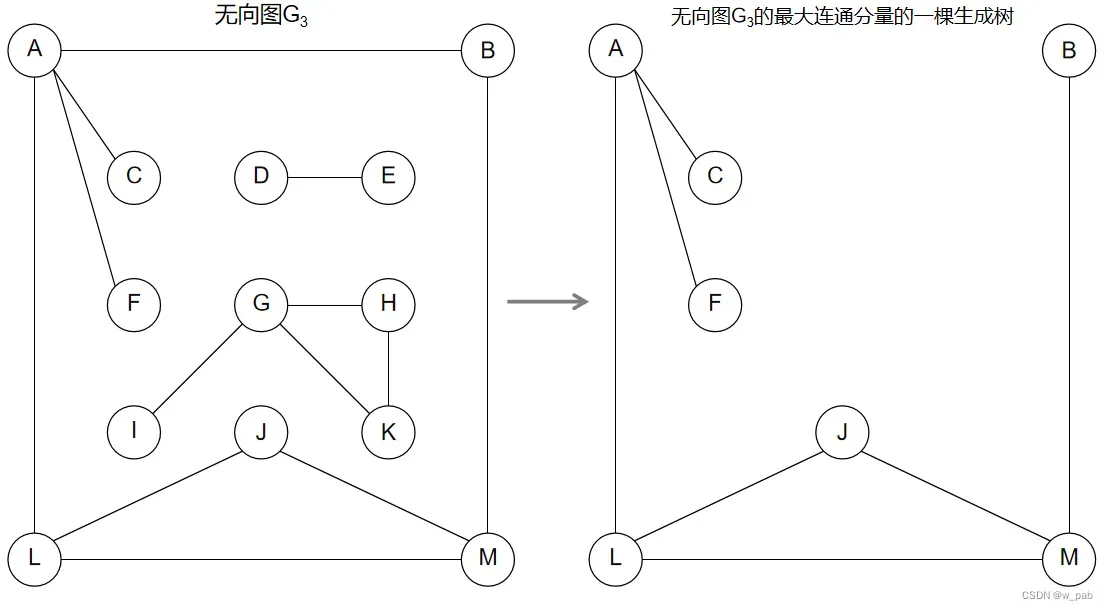
若在上图的生成树中添上一条边,则必定构成一个环。
一棵有n个顶点的生成树仅有n – 1条边。因此:
- 若一个图有n个顶点和少于n – 1条的边,则该图就是非连通图。
- 若一个图有n个顶点和多于n – 1条的边,则该图必定有环。
(注:但是有n – 1条边的图不一定是生成树。)
||| 有向树和生成森林
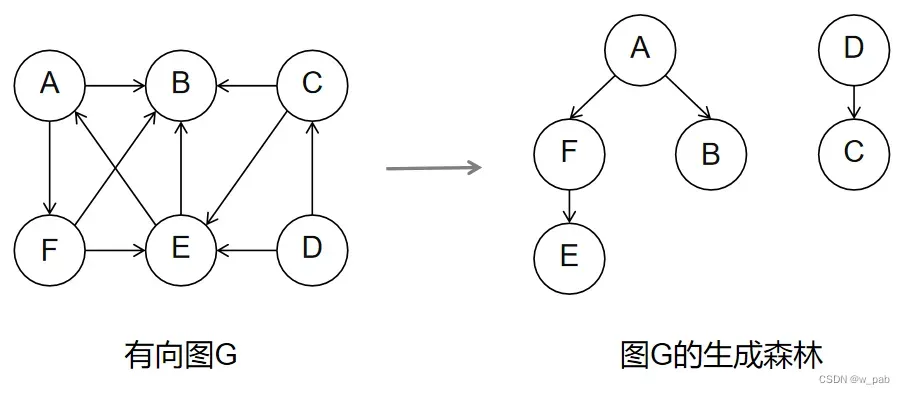
- 有向树:有一个顶点的入度为0,其余顶点的入度均为1的有向图被称为有向树。
- 生成森林:一个有向图的生成森林由若干棵有向树组成(含有图中所有顶点,但是只有可以构成若干不相交的有向树的弧)。
【例子】
图的类型定义
图的抽象数据类型的定义如下:

图的存储结构
由于图的结构的复杂性,无法通过数据元素在存储区中的物理位置来表示元素之间的关系,所以图是没有顺序存储结构的。可以使用二维数组来表示元素之间的关系,即邻接矩阵表示法。
邻接矩阵
1. 邻接矩阵表示法
邻接矩阵是表示顶点之间相邻关系的矩阵。设G(V, E)是具有n个顶点的图,则G的邻接矩阵是具有如下性质的n阶方阵:

【例子】

——
若G是网(带权的图),则可定义邻接矩阵为:

【例子】

图的邻接矩阵存储表示如下:
#define MVNum 50 //最大顶点数
#define MaxInt 32767 //定义权值的最大值(足够大而不会溢出的数)
typedef char VerTexType; //设置顶点的类型
typedef int ArcType; //设置边的权值类型
typedef struct
{
VerTexType vexs[MVNum]; //顶点表
ArcType arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //图当前的顶点数和边数
}AMGraph;在C语言或者C++中,在头文件中规定了各种类型能够取得的最大值,可以自行调用。
2. 使用邻接矩阵表示法创建无向网
【参考代码:CreateUDN函数】
Status CreateUDN(AMGraph& G)
{
//------准备阶段------
cin >> G.vexnum >> G.arcnum; //依次输入总顶点数、总边数
for (int i = 0; i < G.vexnum; i++) //依次输入点的信息
cin >> G.vexs[i];
for (int i = 0; i < G.vexnum; i++) //初始化邻接矩阵,将边的权值均设为最大值
for (int j = 0; j < G.vexnum; j++)
G.arcs[i][j] = MaxInt;
//------构建邻接矩阵阶段------
for (int k = 0; k < G.arcnum; k++)
{
VerTexType v1, v2;
ArcType w;
cin >> v1 >> v2 >> w; //v1、v2是一条边所依附的顶点,w是该条边的权值
int i = LocateAMGVex(G, v1); //确定v1和v2在G中的位置(即顶点数组的下标)
int j = LocateAMGVex(G, v2);
G.arcs[i][j] = w; //将边<v1, v2>的权值置为w
G.arcs[j][i] = G.arcs[i][j]; //设置对称边
}
return true;
}【参考代码:LocateAMGVex函数】
对LocateVex函数的要求:遍历顶点数组的下标,并且返回所求顶点的位置。
int LocateAMGVex(AMGraph G, VerTexType v)
{
for (int i = 0; i < G.vexnum; i++)
{
if (G.vexs[i] == v)
return i;
}
return -1;
}【算法分析】
上述算法的时间复杂度:O(n²) 。(参考上述算法,也可以通过稍加改动得到无向图、有向网、有向图的创建算法。)
3. 邻接矩阵表示法的优缺点
(1)优点
① 通过对A[i][j]的数值进行观察,可以很快判断出两顶点之间是否有边。
② 通过邻接矩阵,可以轻易计算得到各个顶点的度(出度、入度)。
(2)缺点
① 不便于增删顶点;
②不便于统计边的数目(需要遍历邻接链表,时间复杂度为O(n²));
③ 空间复杂度高,是O(n²),对于稀疏图而言尤其浪费空间。
由于上述邻接法的缺点,就需要有更适合稀疏图的数据结构。由此就引入了邻接表。
邻接表
1. 邻接表表示法
邻接表是图的一种链式存储结构。一般地,邻接表有两部分组成:
- 表头结点表:由表头结点组成,通过顺序结构进行存储,方便访问(表头结点用以存储顶点的相关信息)。
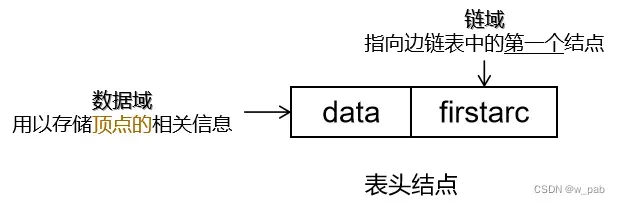
- 边链表:由表示图中关系的2n个边链表组成(边链表由边结点组成)。

由上述数据结构可知:① 在无向图的邻接表中,某顶点的度就是其对应链表中的结点数;② 在有向图中,某一链表中的结点数就是对应结点的出度。但是,若要求得某一结点的入度,就需要遍历整个邻接表。此时为了方便,就需要一个有向图的逆邻链表,如图:
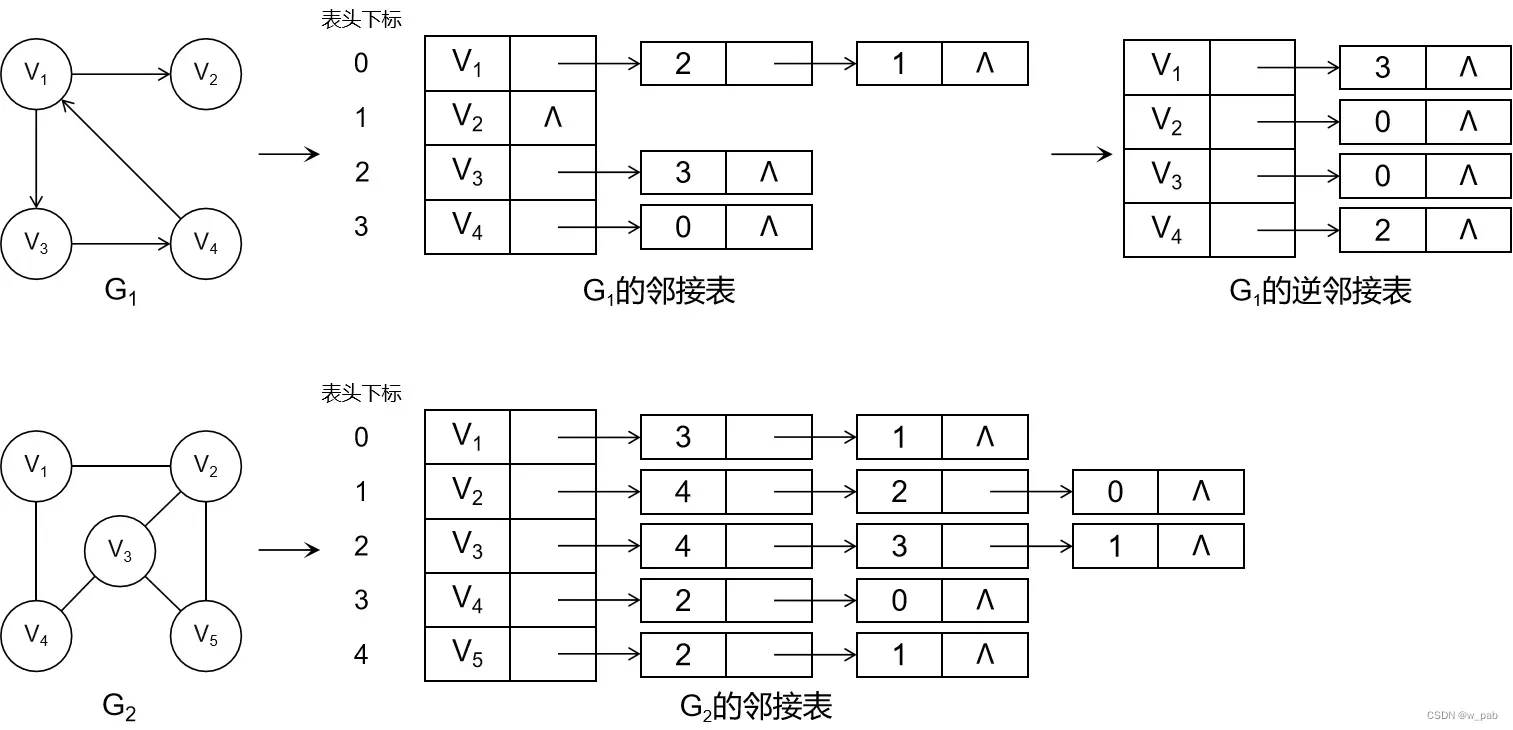
图的邻接表的存储结构(头结点、边结点)可参考下面:
#define MVNum 50 //最大顶点数
#define OtherInfo int //相关信息的类型
typedef struct ArcNode //边结点的存储结构
{
int adjvex; //该条边指向的结点的位置
struct ArcNode* nextarc; //指向与下一条边(对应的结点)
OtherInfo info; //和边有关的信息(例如:权值)
}ArcNode;
typedef struct VNode //顶点信息
{
VerTexType data;
ArcNode* firstarc; //指向与该顶点邻接的第一条边(第一个顶点)
}VNode, AdjList[MVNum];
typedef struct //邻接表
{
AdjList vertices; //表本体
int vexnum, arcnum; //图的当前顶点数和边数
}ALGraph;2. 通过邻接表表示法创建无向图
【参考代码:CreateUDG函数】
Status CreateUDG(ALGraph& G)
{
cin >> G.vexnum >> G.arcnum; //依此输入总顶点数、总边数
for (int i = 0; i < G.vexnum; i++) //输入各个顶点,构造表头结点表
{
cin >> G.vertices[i].data; //输入顶点的值
G.vertices[i].firstarc = NULL; //表头结点的指针域置空
}
for (int k = 0; k < G.arcnum; k++) //输入各边,构造边链表
{
VerTexType v1, v2; //输入一条边依附的两个顶点
cin >> v1 >> v2;
int i = LocateALGVex(G, v1); //确定顶点在G.vertices中的位置(序号)
int j = LocateALGVex(G, v2);
ArcNode* p1 = new ArcNode; //生成新的边结点
p1->adjvex = j; //邻接点的序号就是j
p1->nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc = p1; //将p1插入顶点i边表的表头
ArcNode* p2 = new ArcNode;
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p2; //将p2插入顶点j边表的表头
}
return true;
}【参考代码:LocateALGVex函数】
类似于LocateAMGVex函数,只是在搜索时稍加改动。
int LocateALGVex(ALGraph G, VerTexType v)
{
for (int i = 0; i < G.vexnum; i++)
{
if (G.vertices[i].data == v)
return i;
}
return -1;
}【算法分析】
上述算法的时间复杂度:O(n + e)。(如若需要建立有向图的邻接表,则更加简单。而若要创建有向网的邻接表,则可在info域内输入边的权值。)
注:一个图的邻接矩阵是唯一的,但是邻接表却是不唯一的。
3. 邻接表表示法的优缺点
(1)优点
① 便于增删结点。
② 便于统计边的数目(通过扫描边表即可得到,时间复杂度是O(n + e))。
③ 空间复杂度为O(n + e),空间效率高,适合稀疏图(邻接矩阵表示法更适合稠密图)。
(2)缺点
① 不便于判断顶点之间是否存在边(需要扫描对应边表,最坏情况下时间复杂度为O(n))。
② 不便于计算有向图中各个顶点的度(特别是有向图,为了求得入度,需要遍历各顶点的边表。若采用逆邻接表,则难求出度)。
为了方便求出顶点的入度和出度,接下来就要引入十字链表的概念。
十字链表(有向图)
十字链表是有向图的一种链式存储结构,相当于结合了有向图的邻接表和逆邻接表。十字链表将结点分为了两种 —— 弧结点和边结点:

在十字链表中,弧头相同的弧在同一链表上,弧尾相同的弧也在同一链表上。
【例如】
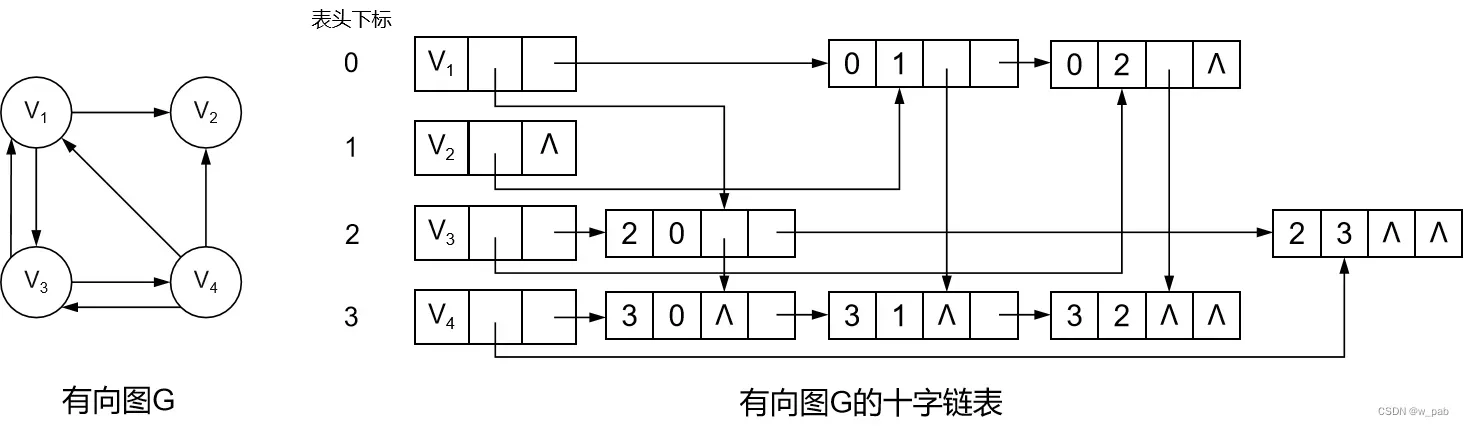
有向图的十字链表存储表示形式可参考下面:
#define MAX_VERTEX_NUM 20
#define InfoType int
typedef struct ArcBox
{
int tailvex, headvex; //该弧的尾和头顶点的位置
struct ArcBox* hlink, * tlink; //分别为弧头相同和弧尾相同的弧的链域
InfoType* info; //关于该弧的相关信息的指针
}ArcBox;
typedef struct VexNode
{
VerTexType data;
ArcBox* firstin, * firstout; //分别指向该顶点的第一条入弧和出弧
}VexNode;
typedef struct
{
VexNode xlist[MAX_VERTEX_NUM]; //表头向量
int vexnum, arcnum; //有向图的当前顶点数和弧数
}OLGraph;如果要进行有向图的十字链表的创建,可以模仿邻接表的创建算法:

建立十字链表的时间复杂度也是O(n + e)。但是十字链表在寻找弧和度上具有更大的优势。
邻接多重表(无向图)
邻接多重表是无向图的一种(很有效的)链式存储结构。由于在邻接表中,一条弧依附的两个顶点分别被存储在不同的链表中,在寻找一条弧对应的两个顶点时存在困难,给某些图的操作带来了不便。所以,就要通过邻接多重表解决这一问题。
类似于十字链表,邻接多重表也由两种不同的结点构成:

【例如】
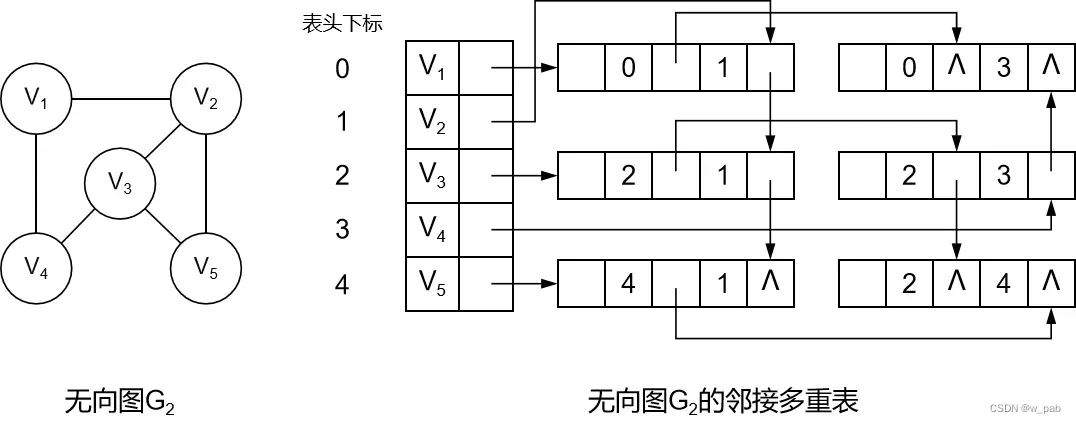
邻接多重表的类型说明如下:
//------无向图的邻接多重表存储表示------
#define MAX_VERTEX_NUM 20
typedef enum { unvisited, visited } VisitIf;
typedef struct EBox
{
VisitIf mark; //是否访问的标记
int ivex, jvex; //该条边依附的两个顶点的位置
struct EBox* ilink, * jlink; //分别指向依附这两个顶点的下一条边
InfoType* info;
}Ebox;
typedef struct VexBox
{
VerTexType data;
Ebox* firstedge; //指向依附于该顶点的第一条边
}VexBox;
typedef struct
{
VexBox adjmulist[MAX_VERTEX_NUM];
int vexnum, edgenum; //无向图的当前顶点数和边数
}AMLGraph;邻接多重表的各种基本操作的实现和邻接表类似,实现时可以参考邻接表。

图的遍历
类似于树的遍历,图的遍历也需要从某一结点出发,按照某种方式对图中所有结点进行(仅一次的)访问。但是,图的遍历可能会涉及回路等的问题,这意味着在沿某条路径进行访问时,有可能回到最开始进行访问的结点。为此,就需要对已访问的结点进行标记:
- 一般地,设辅助数组visited[n];
- 辅助数组的初始值均为 0(“false”);
- 将已经过的某一结点对应的visited[i]设为 1(“true”)。
根据搜索路径方向的不同,通常会有两种不同的遍历图的路径:深度优先搜索和广度优先搜索。
深度优先搜索(DFS)
深度优先搜索可以看作是树的先序遍历的一种推广。其的过程用例子表示如下:


![]()
由上图可得到一棵深度优先生成树,如图:
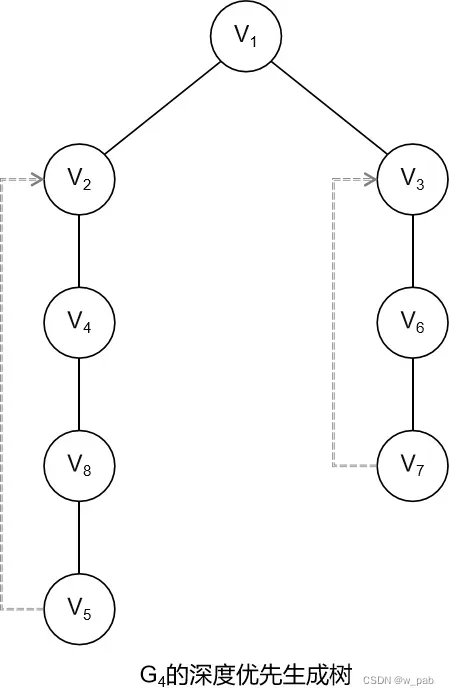
【参考代码:DFS函数,深度优先搜索访问连通图的(递归)算法实现】
//------深度优先搜索遍历连通图(以无向图为例,使用邻接表存储)------
void DFS(ALGraph G, int v) //从第v个顶点开始访问
{
cout << G.vertices[v].data; //访问(此处为输出)第v个顶点
visited[v] = true; //在标志数组相应位置进行标记
for (int w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w))
{
if (!visited[w]) //对尚未访问的邻接顶点w进行访问
DFS(G, w);
}
}除DFS函数之外,还牵扯到两个函数:FirstAdjVex() 和 NextAdjVex() ,它们的作用分别是:
▪ FirstAdjVex函数:检查v的所有邻接点w,返回v的第一个邻接点;
▪ NextAdjVex函数:返回v相对于w的下一个邻接点。
由于篇幅有限,下面将仅展示通过邻接表实现的这两个函数。
【参考代码:FirstAdjVex函数】
int FirstAdjVex(ALGraph G, int v)
{
if (G.vertices[v].firstarc) //遍历边表
return G.vertices[v].firstarc->adjvex;
else
return -1; //邻接点不存在
}【参考代码:NextAdjVex函数】
int NextAdjVex(ALGraph G, int v, int w)
{
ArcNode* p = G.vertices[v].firstarc;
while (p && p->adjvex != w) //寻找w指示顶点
p = p->nextarc;
if (p && p->nextarc)
return p->nextarc->adjvex;
else
return -1;
}注意:上述的情况没有涉及到非连通图的处理。也就是说,当上述遍历执行完毕后,非连通图中一定会有未被访问的顶点。此时需要在图中再次寻找新的起始点(即仍未被访问的结点),再次执行上述步骤,直到图中所有顶点均被访问完毕。
【参考代码:深度优先搜索遍历非连通图(邻接表版本)】
//------对非连通图G进行深度优先搜索------
void DFSTraverse(ALGraph G)
{
for (int v = 0; v < G.vexnum; v++) //初始化标志数组
visited[v] = false;
for (int v = 0; v < G.vexnum; v++)
if (!visited[v]) //对尚未访问过的顶点进行函数调用
DFS(G, v);
}对于DFSTraverse函数,每调用一次DFS_AL函数,就代表着有一个连通分量。
【算法分析:DFSTraverse函数(以邻接表为例)】
在遍历时,一个顶点只访问一次,之后就不会从该顶点出发进行搜索。故遍历图的实质就是对每个顶点查找其邻接点的过程。设图中顶点数为 n ,边数为 e ,则在邻接表中:
- 查找邻接点的时间复杂度为:O(e);
- 深度优先搜索遍历图的时间复杂度为:O(n + e)。
在邻接矩阵中,查找邻接点的时间复杂度为O(n²)。
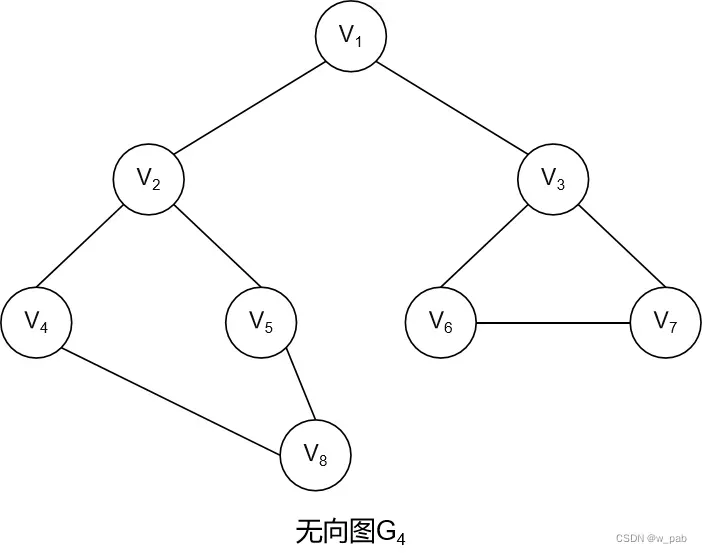
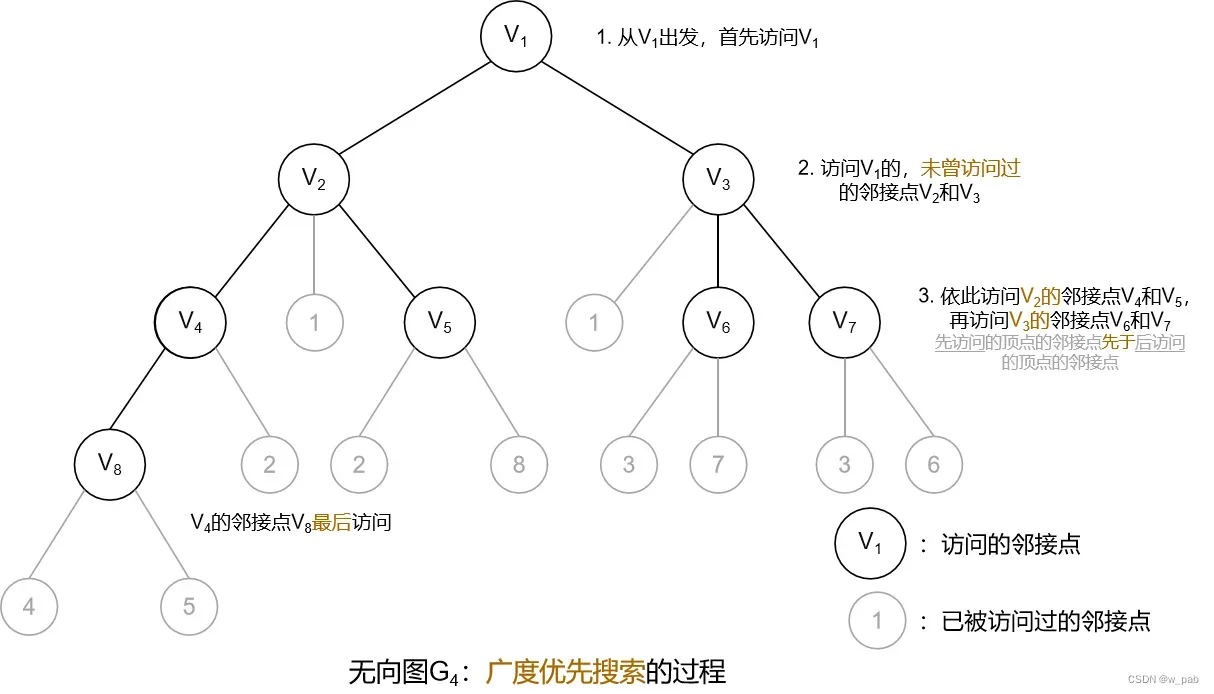
广度优先搜索(BFS)
广度优先搜索类似于数的按层次遍历,依旧以无向图G₄为例:
![]()
同样的,通过上述方法可以得到一棵广度优先生成树,如图:

【参考代码:BFS函数,广度优先搜索遍历连通图(依旧以邻接表为例)】
在这种类似于层次遍历的算法中,先访问的顶点,其邻接点也会被优先访问。因此,需要引入队列保存以被访问过的结点。
另外,该算法同样需要一个标志数组。
void BFS(ALGraph G, int v)
{
cout << G.vertices[v].data; //访问第v个顶点,并且通过标志数组进行标记
visited[v] = true;
SqQueue Q;
InitQueue(Q); //初始化队列Q
EnQueue(Q, v); //v进队
while (!QueueEmpty(Q)) //若队列非空
{
int u = 0;
DeQueue(Q, u); //弹出队头元素
for (int w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w))
{//依此检查u的所有邻接点
if (!visited[w]) //若w是u未被访问的邻接点
{
cout << G.vertices[w].data;
visited[w] = true; //访问,并置标记
EnQueue(Q, w); //w进队
}
}
}
}若为非连通图,则该算法也一定会有无法访问到的顶点。此时就需要另寻未被访问过的顶点,重复上述广度优先搜索过程:

这和深度优先算法很类似,仅需将DFS函数替换为BFS函数即可。
【算法分析:BFSTraverse函数】
因为每个顶点最多仅一次进入队列,故该算法实质上就是通过边寻找邻接点的过程。类似于深度优先算法,当使用邻接表存储时,该算法的时间复杂度为O(n + e)(同样的,若使用邻接矩阵存储,则时间复杂度为O(n²))。
版权声明:本文为博主作者:w_pab原创文章,版权归属原作者,如果侵权,请联系我们删除!
