定义
二叉判定树是用于描述解决问题的思路,比如可以使用判定树描述N个数的比较过程,是一种对过程的描述。
它也可以用于描述二分查找(即折半查找,以下都作二分查找)的过程。
描述二分查找的二叉判定树,我们也可以叫折半查找判定树,
从这样的判定树,我们可以分析二分查找算法的效率
如何构造长度为n的折半查找判定树
- 当n=0时,折半查找判定树为空;
- 当n>0时,折半查找判定树的根结点是有序表中序号为mid=(n+1)/2的记录,根结点的左子树是与有序表r[1] ~ r[mid-1]相对应的折半查找判定树,根结点的右子树是与r[mid+1] ~ r[n]相对应的折半查找判定树。
画出长度为18的顺序储存的有序表进行折半查找时的判定树,并求平均查找长度
首先找根节点:mid = (18+1) / 2 = 9 (向下取整)
判断左子树: 左子树的查找范围是(1 ~ 8),mid = ( 1 + 8 ) / 2 = 4
判断右子树: 右子树的查找范围是(10 ~ 18),mid = ( 10 + 18 ) / 2 = 14
递归进行下去,得到结果:
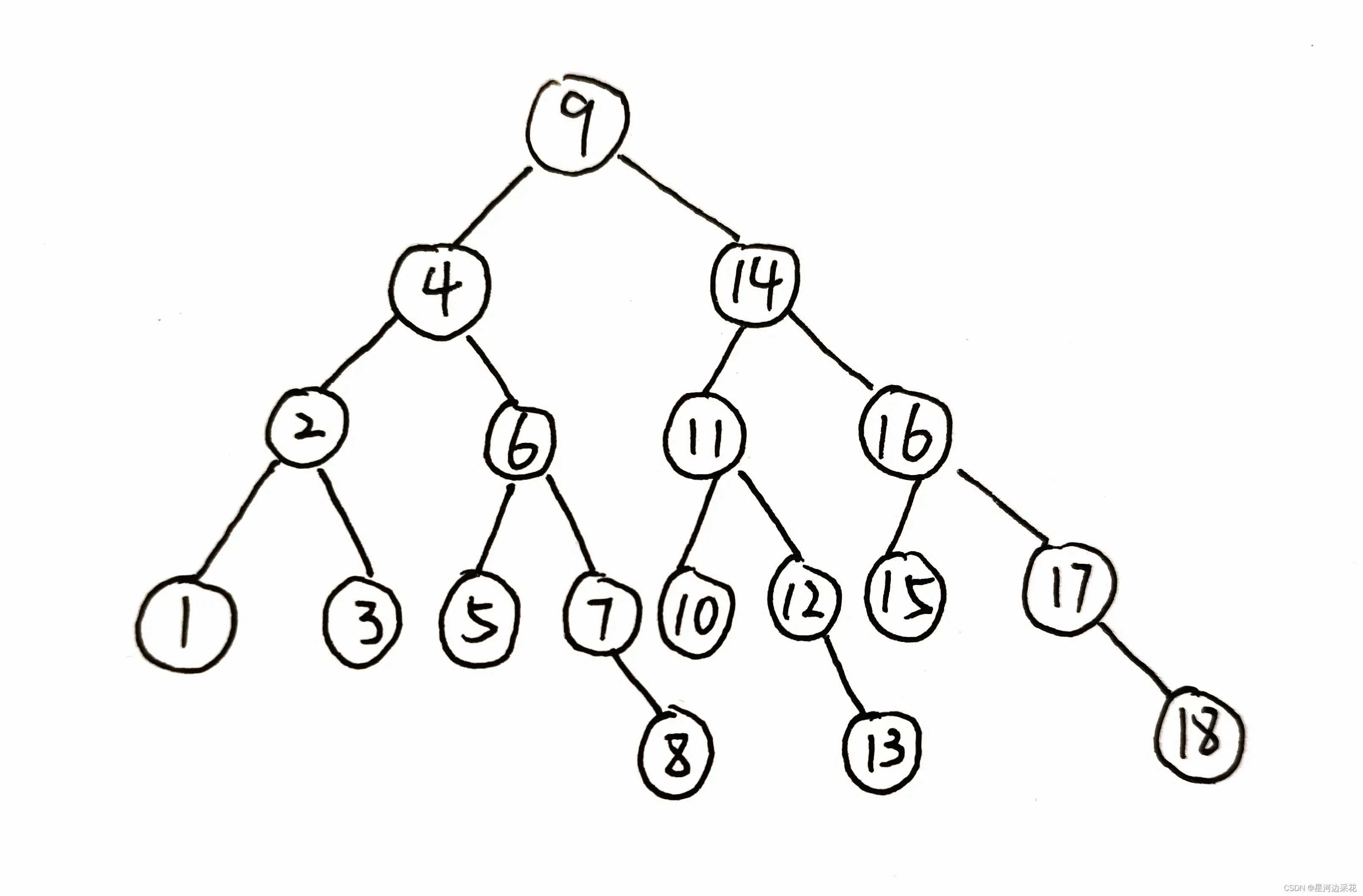
平均查找长度:(1 + 2*2 + 4*3 + 8*4 + 3*5)/ 18 = 32 / 9
拓展
我们刚刚做出的这个判定树是采取了向下取整,但向上向下都是可以的,
必须注意的一点是:在一颗判定树中,要向下取整,全都向下取整,不能混有向上取整
折半查找判定树的中序遍历,刚好是原来那些数排好序的样子
版权声明:本文为博主作者:星河边采花原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/qq_59183443/article/details/128199099
