数据结构:完全二叉树开胃菜小练习

目录

一.前言

关于树及完全二叉树的基础概念(及树结点编号规则)参见:http://t.csdn.cn/imdrahttp://t.csdn.cn/imdra

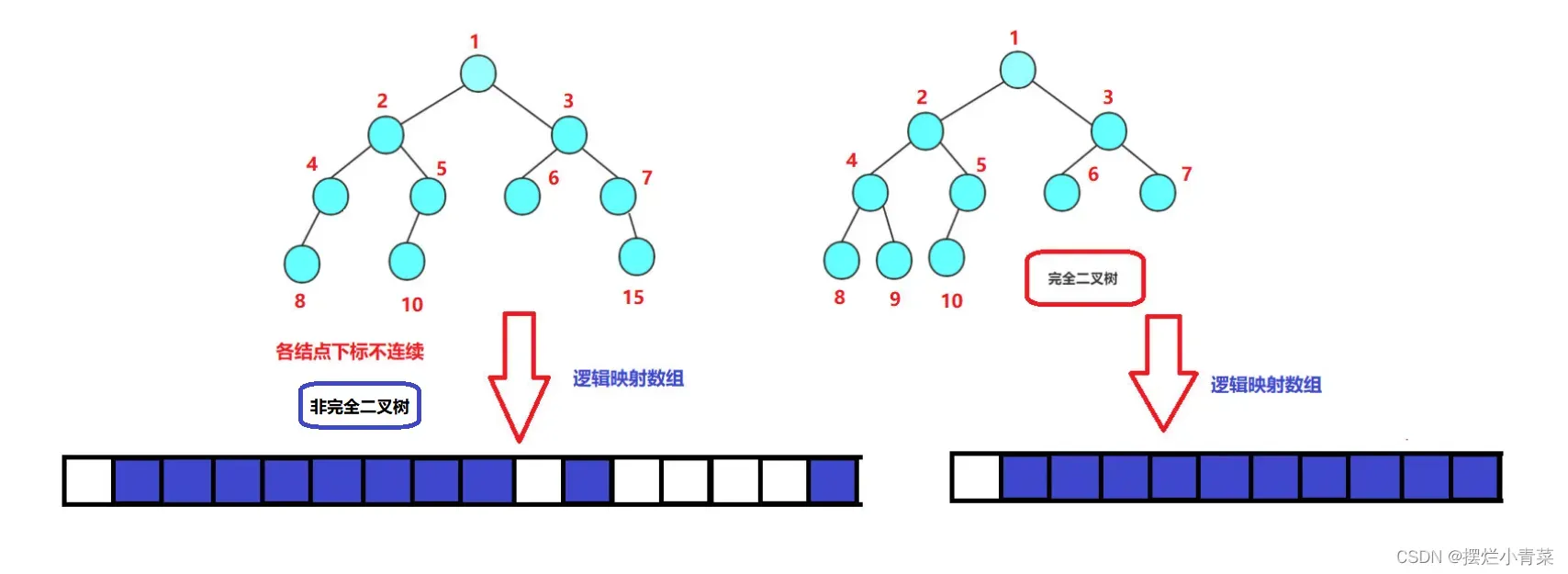
完全二叉树是一种非常重要的数据结构:

n个结点的完全二叉树的结点编号是从0~(n-1)连续排列的(假设根结点的编号为0),因此将完全二叉树映射到内存中线性存储结构中时内存利用效率十分的高(数组下标和树结点编号建立绝对映射关系).

最经典的完全二叉树线性存储结构就是大小根堆(堆排序的数据结构基础)

二.完全二叉树的重要结构特点

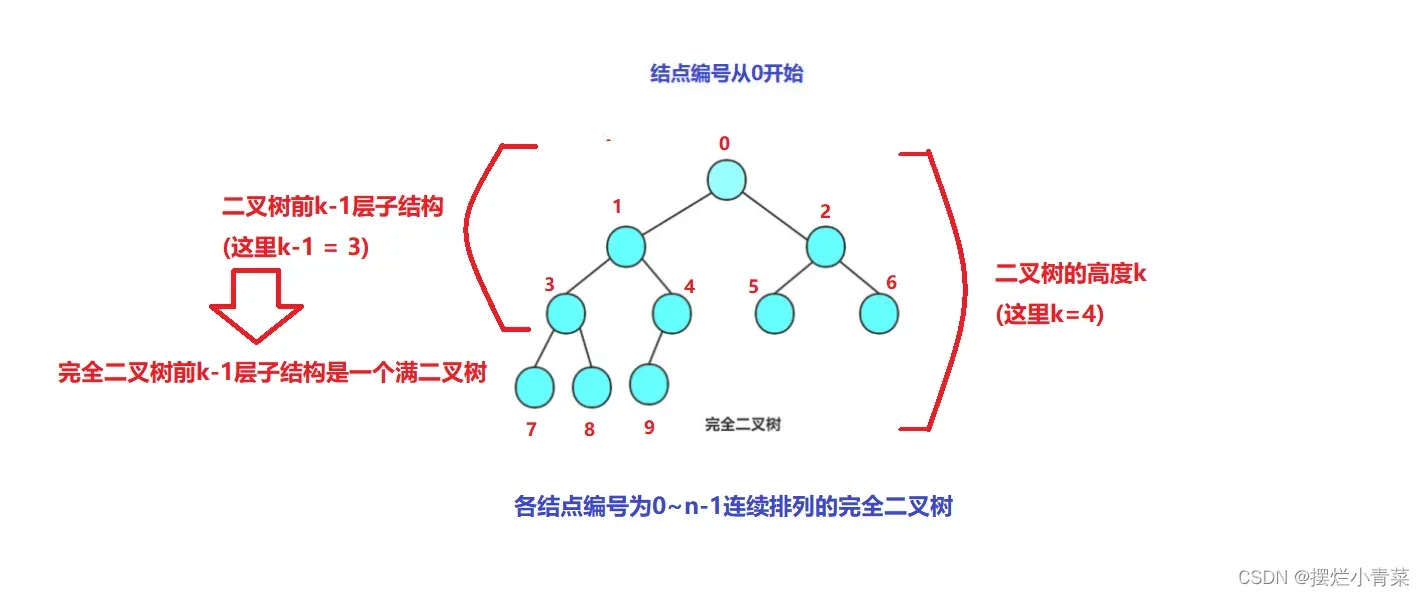
• 假设一个结点总数为n完全二叉树T的高度为k,为了满足各结点编号是0~(n-1)连续排列的结构定义,完全二叉树1~(k-1)层所有结点构成的子结构是一颗满二叉树(也就意味着完全二叉树的所有叶结点都分布在树的最后一层(第k层)):
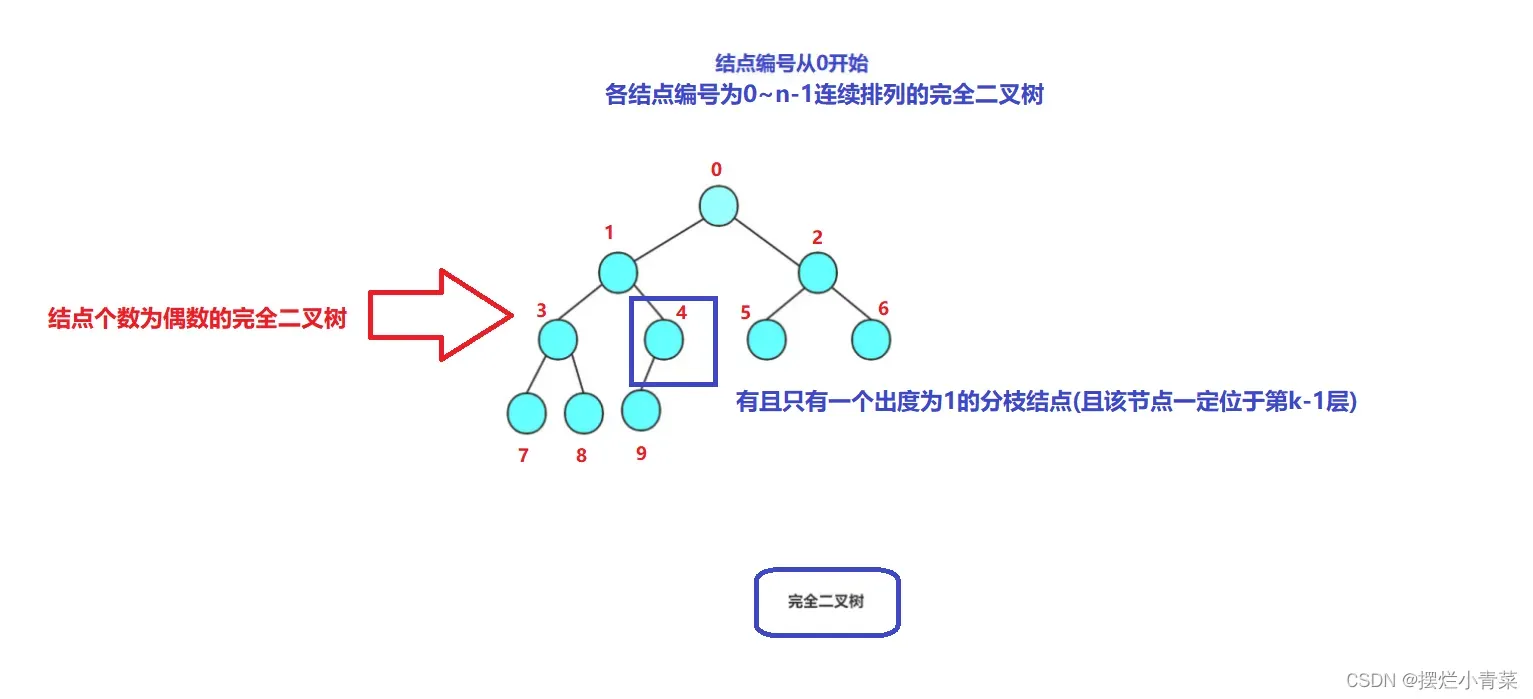
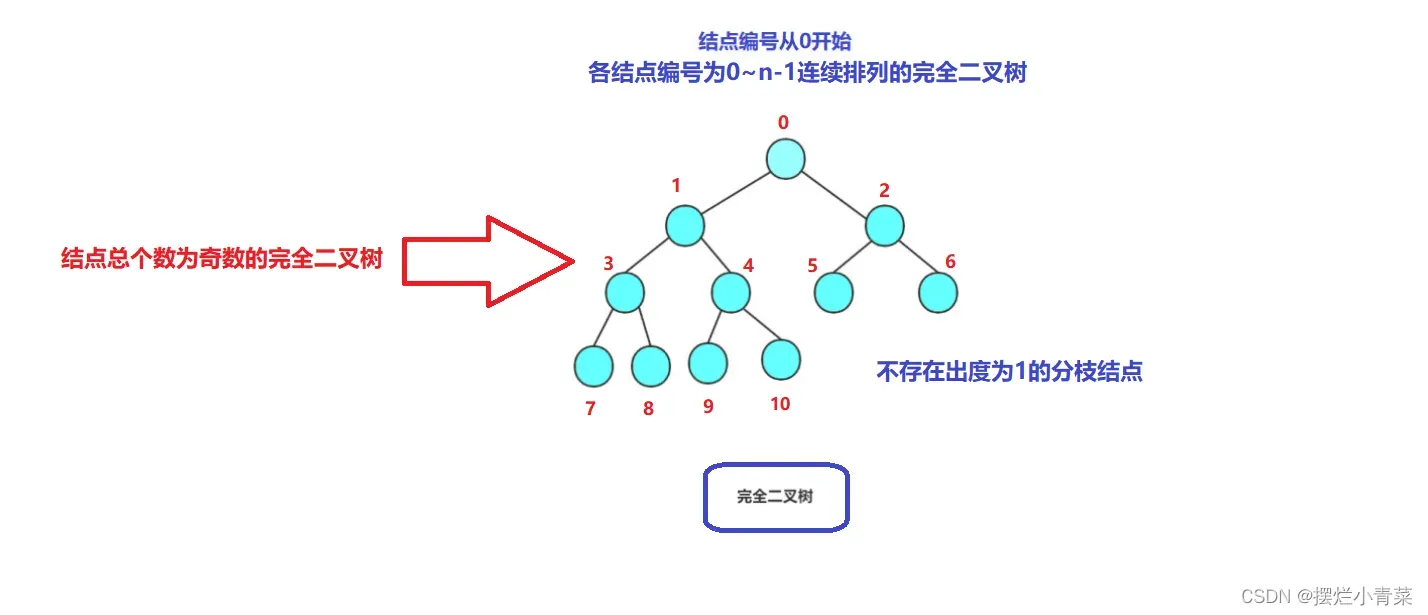
• 假设一个结点总数为n完全二叉树T的高度为k,为了满足各结点编号是0~(n-1)连续排列的结构定义,完全二叉树的第k层(最后一层)的叶节点必须是连续排列的(也就是意味着结点总数为奇数的完全二叉树不存在出度为1的分枝结点,结点总数为偶数的完全二叉树有且仅有一个出度为1的分枝结点)

三.完全二叉树开胃菜小练习

1.一个重要的数学结论

• 对任何一棵二叉树, 如果出度为0其叶结点个数为N0, 出度为2的分枝结点个数为N2(包括根) ,则有 N0＝ N2＋1

该结论具体证明参见小青菜的博客 :http://t.csdn.cn/imdrahttp://t.csdn.cn/imdra

2.简单的小练习

• 现有一颗具有 2n 个结点的完全二叉树T,求其叶结点的个数

求解:

设T出度为0的结点个数为N0(即叶结点的个数),

出度为1的结点个数为N1,

出度为2的结点个数为N2。

根据本篇第二章中的结构分析可知,N1要么为1,要么为0

1. 若N1 = 0,根据关系式N0 = N2 + 1,可得:2n = N0 + N1 + N2,化简可得N0 = (2n+1)/2，N0不为整数,因此该种情况排除
2. 若N1 =1,根据关系式N0 = N2 + 1,可得:2n = N0 + N1 + N2,化简可得N0 = n,满足题意

因此T叶节点个数为n

• 一棵完全二叉树的结点总数为531个，求这棵树的高度

求解：

设该树的高度为k

根据本篇第二章中的结构分析可知,该树前k-1层构成一颗满树(根据等比数列求和公式满树总结点个数为2^(k-1)-1)

而2^9 = 512<531<2^10 = 1024,因此k-1 = 9,可以求得该二叉树的高度为10

• 现有一颗具有767个结点的完全二树T，求其叶子结点个数

求解:

设T出度为0的结点个数为N0(即叶结点的个数),

出度为1的结点个数为N1,

出度为2的结点个数为N2。

根据本篇第二章中的结构分析可知,N1要么为1,要么为0

1. 若N1 = 0,根据关系式N0 = N2 + 1,可得:767 = N0 + N1 + N2,化简可得N0 = 384，满足题意
2. 若N1 =1,根据关系式N0 = N2 + 1,可得:767 = N0 + N1 + N2,化简可得N0 = 767/2,N0不为整数,因此该种情况排除

因此T叶节点个数为384