文章目录
一、问题定义
1.1 二叉搜索树
二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉搜索树。
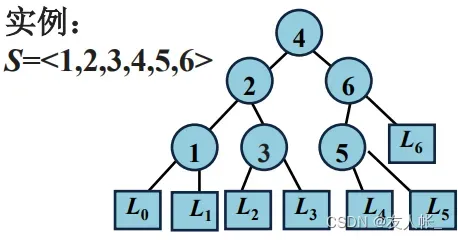
规定树根为第0层,圆结点为数据,方结点为数据之间的空隙。
1.2 概率分布
实际上每个数据出现的概率是不同的,给定序列,构造二叉搜索树,形成了
个结点
,和
个空隙
,其中
记在
出现的概率为
,在空隙
的概率为
,则
的存取概率分布为
1.3 检索数据的平均时间
对于数据集和存取概率分布
:
规定树根为第0层,结点在
中的深度是
,空隙
的深度为
,平均比较次数为:
例如,给定树:
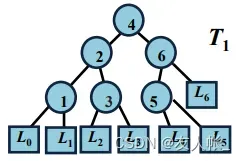
,
(
用**包围)
则平均检索时间为:
1.4 最优二叉搜索树问题
对于数据集和存取概率分布
,不同的树的组织形式会产生不同的平均检索时间,如何求一棵平均比较次数最少的二叉搜索树?
二、算法
2.1 分析问题结构
以为界划分子问题:
令,存取概率分布:
2.2 建立递推关系
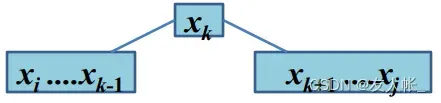
假设以作为树的根,则树被划分为三部分:
左子树:
根:
右子树:
令,表示
到
之间所有概率(数据和空隙)之和;设
是相对于输入
和
的最优二叉搜索树的平均比较次数
则可建立递推方程:
(1)为了不遗漏最优解,所以需要从
到
依次选取做根尝试,选出最小值
(2)
表示以
做根的最优左子树的比较次数
(3)
表示以
做根的最优右子树的比较次数
(4)对于给定的数据
,需要先与根
进行比较后才可以进入到左子树或右子树;而由于使用根
将左子树和右子树连接起来,子树的每个结点高度均增加了一层,所以在比较次数上也要加1,所以
是由增加的左子树的比较次数、增加的右子树的比较次数、和根的比较次数之和
的证明:
由根引起的比较次数增加为:
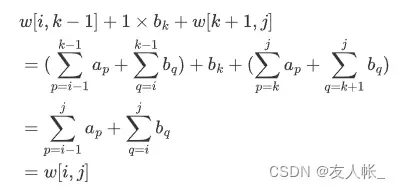
2.3 自底向上计算
初始化:当左子树或右子树为空时,其平均查找数为0
不妨以来观察:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | NULL | NULL | NULL | NULL | NULL |
| 1 | 0 √ | √ | √ | √ | ※ |
| 2 | NULL | 0 | √ | ||
| 3 | NULL | NULL | 0 | √ | |
| 4 | NULL | NULL | NULL | 0 | √ |
| 5 | NULL | NULL | NULL | NULL | √ |
显然,要计算一个值,我们需要计算它一行一列的数据,因此确定计算顺序:
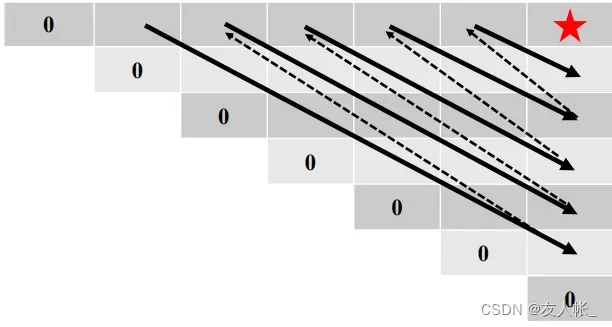
2.4 追踪最优方案
构造追踪数组,
表示
的根节点
。
在计算的过程中,选出最小的
,记录
追踪时,从出发,假设
,则说明在
处进行了分割,分为子树
和
,再分别查看
和
…
如此寻找直至对角线部分。
2.5 复杂度分析
时间复杂度
空间复杂度
版权声明:本文为博主作者:友人帐_原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/m15253053181/article/details/128895617
