数据结构——网状关系
- 🍃网状结构
- 🍃网状关系的顺序存储
-
- 🌿无向无权图
- 🌿有向无权图
- 🌿无向有权图
- 🌿有向有权图
- 🍃网状关系的链式存储
-
- 🌿十字链表法
- 🍃遍历
-
- 🌿佛洛依德算法
-
- 🍀原理
- 🍀例子
🍃网状结构
按有无方向分:有向图、无向图
按是否有权值:带权图、不带权图
🍃网状关系的顺序存储
🌿无向无权图
(有路径1,无路径0)

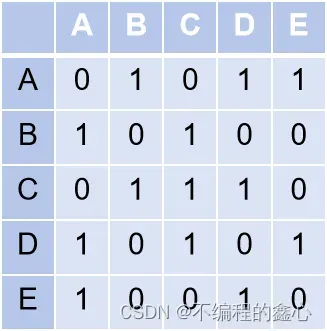
🌿有向无权图
(有路径1,无路径0)
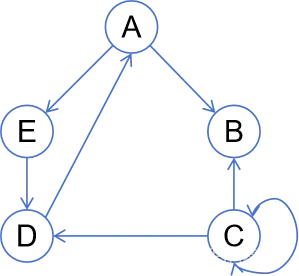

🌿无向有权图
(有路径存路径,无路径存“/”)
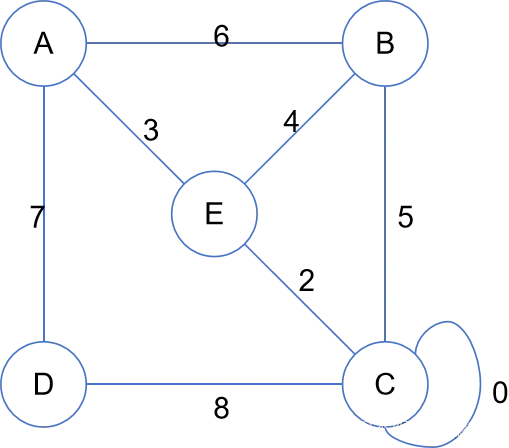

🌿有向有权图
(有路径存路径,无路径存“/”)


🍃网状关系的链式存储
🌿十字链表法
十字链表(Orthogonal List)是有向图的一种链式存储结构。可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表。在十字链表中,对应于有向图中每一条弧有一个结点,对应于每个顶点也有一个结点。
定义
#define MaxVertexTypeNum 100
typedef char VertexType;
typedef int EdgeType;
typedef struct ArcNode{ //边表节点
int tailvex,headvex; //尾域和头域
struct ArcNode *hlink , *think; //出单链表和入单链表
//InfoType info; //权值
}ArcNode; //边表节点的类型
typedef struct VNode{ //顶点表节点
VertexType data; //顶点的数据
ArcNode *firstin,*firstout; //入单链表的头指针和入单链表的头指针
}VNode; // 邻接表类型
typedef struct{ //十字链表
VNode xlist[MaxVertexTypeNum]; //所有结点的数据
int vexnum,arcnum; //节点数和边数
}ALGraph; //十字链表的类型
顶点表结点
| data | dirstin | firstout |
|---|
- data:顶点数据域
- firstin:入边单链表头指针
- firstout:出边单链表头指针
边表结点
| tailvex | headvex | hlink | tlink | info |
|---|
- tailvex:尾域,存放弧尾节点
- headvex:头域,存放弧头节点
- hlink:弧头相同的下一条边,即指向下一个边表节点的指针
- tlink:弧尾相同的下一条边
- info:权值
🍃遍历
🌿佛洛依德算法
🍀原理
Floyd算法可以给出网络中任意两个节点之间的最短路径,因此它是比Dijkstra更一般的算法。Floyd算法的思想是将n个节点的网络表示为
n行n列的矩阵,而矩阵中的元素(i,j)表示从节点i到节点j的距离dij,如果两点直接没有边相连,则相应的元素就是无穷∞。
🍀例子
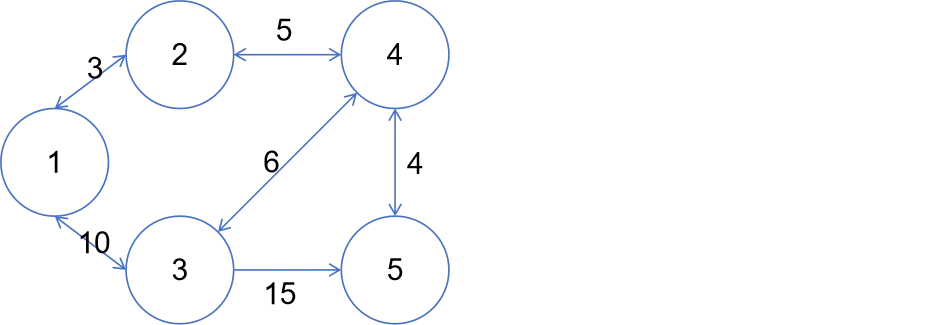
迭代0:D0与S0代表初始形态
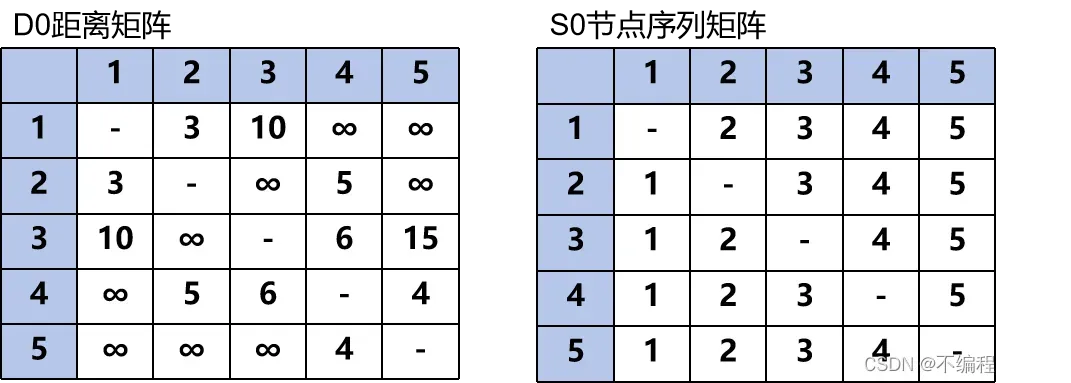
迭代1:看第一行与第一列
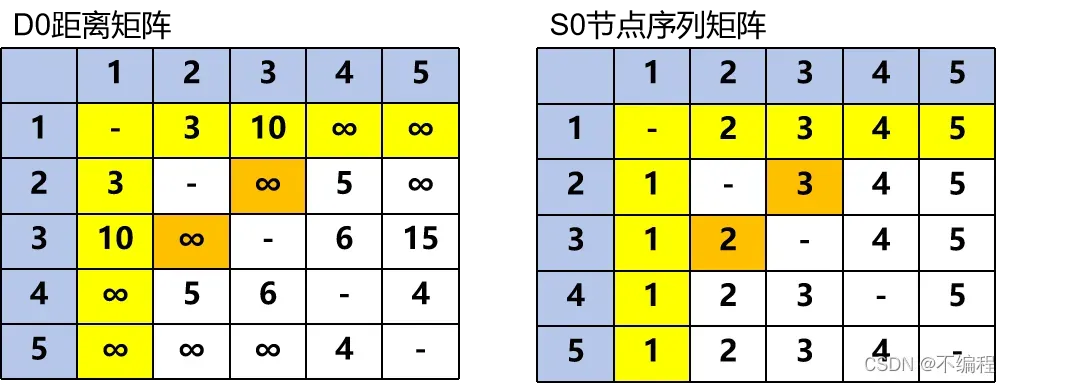
在D0中
橘色区域的值小于横竖的黄色区域相加的值
那么我们将相加后的值替换橘色区域
在S0中的对应位置我们迭代的次数替换进入
由此我们可以得到D1与S1
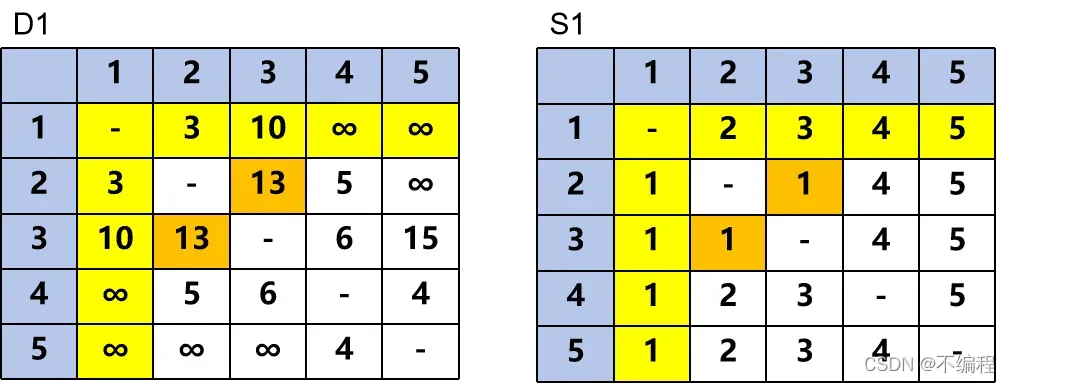
迭代2:看第二行与第二列
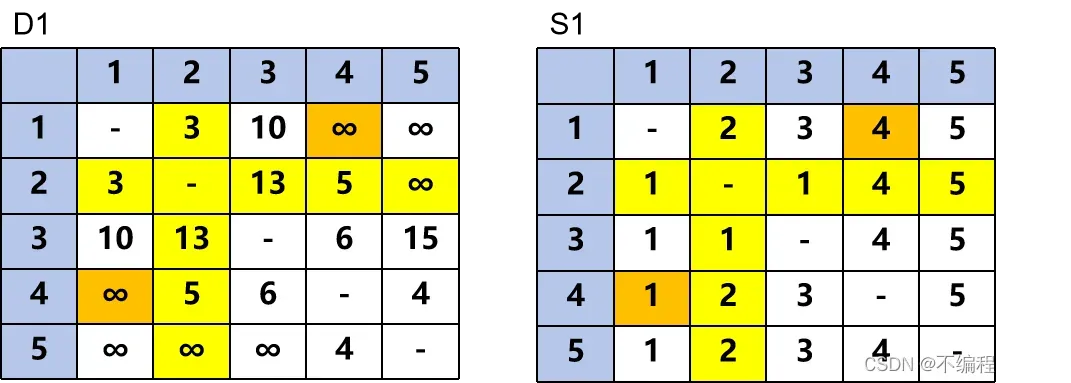
与第一次迭代相同
在D1中
橘色区域的值小于横竖的黄色区域相加的值
那么我们将相加后的值替换橘色区域
在S1中的对应位置我们迭代的次数替换进入
由此我们可以得到D2与S2

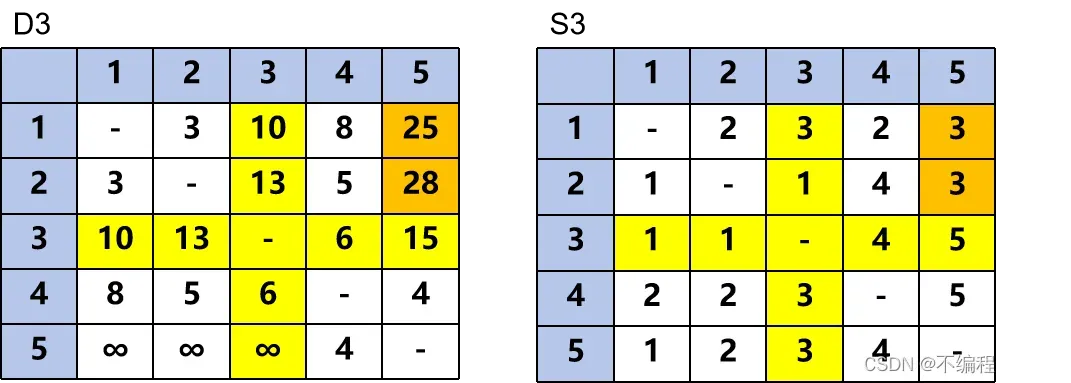
迭代3:看第三行第三列

相同操作得到D3 S3
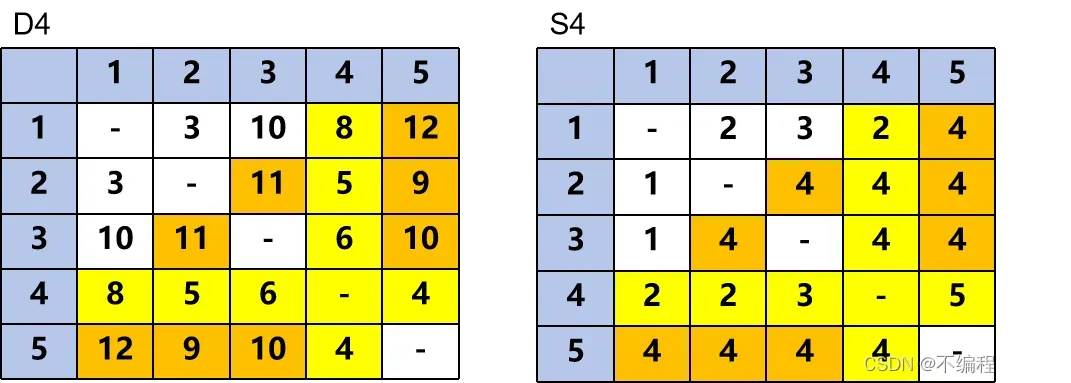
迭代4:看第四行第四列

得到D4 S4
迭代5:看第五行第五列
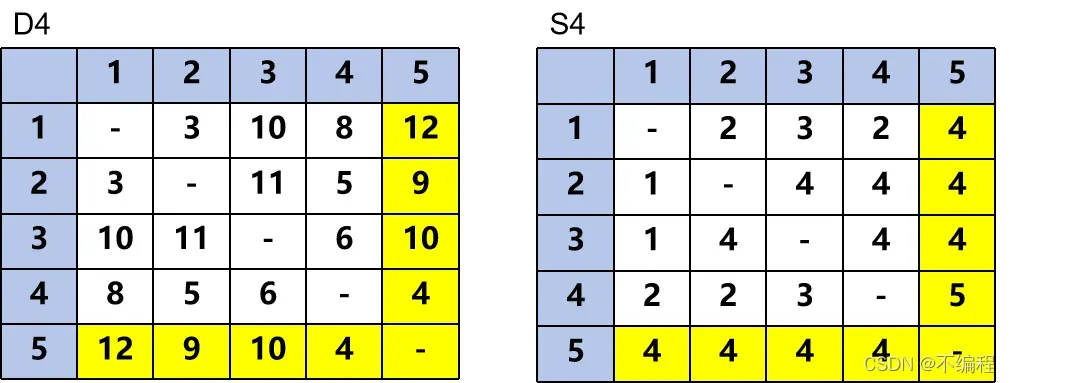
发现没有可以更改的地方可以得出最终D S

这两个矩阵包含了网络中任意两个节点最短路径的所有信息
比如要找节点1到节点5的最短距离
从D中可以找到D15 = 12则最短距离是12
在看S表
S15的前置节点是4
则找S14的前置节点是2
则找S12的前直接点是1
则可以找到最短路径是1 –> 2 –> 4 –> 5
版权声明:本文为博主作者:不编程的鑫心原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/m0_72168217/article/details/136651351
