1. AI技术聚合首页
  2. IT

Python数学建模算法与应用（司守奎）–第4章随笔

xiaoxingxing • • IT • 阅读 67

第 4 章  线性规划和整数规划模型

4.1 线性规划（Linear Programming，LP）

4.1.1 线性规划模型

线性规划模型的一般形式

\text{max(or min)}z=c_{1}x_{1}+c_{2}x_{2}+\cdots+c_{n}x_{n}，

\text{s.t.} \left\{ \begin{matrix} a_{11}x_{1}+a_{12}x_{2}+\cdots+a_{1n}x_{n}\leqslant(or =,\geqslant)b_{1},\hfill \\ a_{21}x_{1}+a_{22}x_{2}+\cdots+a_{2n}x_{n}\leqslant(or =,\geqslant)b_{2},\hfill \\ \cdots\\ a_{m1}x_{1}+a_{m2}x_{2}+\cdots+a_{mn}x_{n}\leqslant(or =,\geqslant)b_{m},\hfill \\ x_{1},x_{2}\cdots,x_{n}\geqslant0 \hfill \end{matrix} \right.

或简写为

\text{max}\left(or\ \text{min} \right )z=\sum\limits_{j=1}^{n}c_{j}x_{j},

\text{s.t.} \left\{ \begin{matrix} \sum\limits_{j=1}^{n}a_{ij}x_{j}\leqslant\left(or \ =,\geqslant \right )b_{i},i=1,2,\cdots,m,\\ x_{j}\geqslant0,j=1,2,\cdots,n. \hfill \end{matrix} \right.

其向量表示形式为

\text{max}\left(or\ \text{min} \right )\textit{\textbf{z}}=\textit{\textbf{c}}^{T}\textit{\textbf{x}}

\text{s.t.} \left\{ \begin{matrix} \sum\limits_{j=1}^{n}\textit{\textbf{P}}_{j}x_{j}\leqslant\left(or \ =,\geqslant \right )\textit{\textbf{b}},\\ \textit{\textbf{x}}\geqslant0. \hfill \end{matrix} \right.

其矩阵表示形式为

\text{max}\left(or\ \text{min} \right )\textit{\textbf{z}}=\textit{\textbf{c}}^{T}\textit{\textbf{x}}

\text{s.t.} \left\{ \begin{matrix} \textit{\textbf{A}}\textit{\textbf{x}}\leqslant\left(or \ =,\geqslant \right )\textit{\textbf{b}},\\ \textit{\textbf{x}}\geqslant0. \hfill \end{matrix} \right.

其中，\textit{\textbf{c}}=\left[c_{1},c_{2},\cdots,c_{n} \right ]^{T} 为目标函数的系数向量，又称为价值向量；

\textit{\textbf{x}}=\left[x_{1},x_{2},\cdots,x_{n} \right ]^{T} 为决策向量；

\textit{\textbf{A}}=\left(a_{ij} \right )_{m\times n} 为约束方程组的系数矩阵；

\textit{\textbf{P}}_{j}=\left[a_{1j},a_{2j},\cdots,a_{mj} \right ]^{T},j=1,2,\cdots,n  为 \textit{\textbf{A}} 的列向量，又称约束方程组的系数向量；

\textit{\textbf{b}}=\left[b_{1},b_{2},\cdots,b_{m} \right ]^{T} 为约束方程组的常数向量。

4.1.2 模型求解及应用

可以使用 Python 的 cvxpy 库，用于求解凸优化问题。http://www.vcxpy.org/

例 4.2 求解线性规划模型

\text{max}z=70x_{1}+50x_{2}+60x_{3} \\ \text{s.t.}\left\{\begin{matrix} 2x_{1}+4x_{2}+3x_{3}\leqslant150,\\ 3x_{1}+x_{2}+5x_{3}\leqslant160,\hfill\\ 7x_{1}+3x_{2}+5x_{3}\leqslant200,\\ x_{i}\geqslant0,i=1,2,3.\hfill \end{matrix}\right.

# 程序文件 ex4_2.py
import cvxpy as cp
from numpy import array
c = array([70, 50, 60])                      # 定义目标向量
a = array([[2, 4, 3],[3, 1, 5], [7, 3, 5]])  # 定义约束矩阵
b = array([150, 160, 200])                   # 定义约束条件的右边向量
x = cp.Variable(3, pos=True)                 # 定义 3 个决策变量
obj = cp.Maximize(c@x)                       # 构造目标函数
cons = [a@x<=b]                              # 构造约束条件
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')                 # 求解问题
print('最优解为：', x.value)
print('最优值为：', prob.value)

例 4.3 某部分今后 5 年考虑以下投资项目，已知：

项目A，从第一年到第四年每年年初需投资，并于次年末收回本利 115%。

项目B，从第三年初需投资，到第五年末能回收本利125%，最大投资额不超过4万元。

项目C，第二年初需投资，到第五年末能收回本利140%，最大投资额不超过3万元。

项目D，五年内每年初购买，于当年末归还，利息收益6%。

部门现有资金10万元，试问如何确定这些项目每年投资额，使第五年末本利总额最大？

建立线性规划模型

\text{max}z=1.15x_{41}+1.40x_{23}+1.25x_{32}+1.06x_{54,} \\ \text{s.t.}\left\{\begin{matrix} x_{11}+x_{14}=100000,\hfill \\ x_{21}+x_{23}+x_{24}=1.06x_{14},\hfill \\ x_{31}+x_{32}+x_{34}=1.15x_{11}+1.06x_{24},\\ x_{41}+x_{44}=1.15x_{21}+1.06x_{34}, \hfill \\ x_{54}=1.15x_{31}+1.06x-{44},\hfill \\ x_{32}\leqslant40000,x_{23}\leqslant30000,\hfill \\ x_{ij}\geqslant0,i=1,2,3,4,5;j=1,2,3,4.\hfill \end{matrix}\right.

# 程序文件 ex4_3.py
import cvxpy as cp
x = cp.Variable((5, 4), pos=True)
obj = cp.Maximize(1.15*x[3, 0]+1.40*x[1, 2]+1.25*x[2, 1]+1.06*x[4, 3])
cons = [x[0, 0]+x[0, 3] == 100000,
       x[1, 0]+x[1, 2]+x[1, 3] == 1.06*x[0, 3],
       x[2, 0]+x[2, 1]+x[2, 3] == 1.15*x[0, 0]+1.06*x[1, 3],
       x[3, 0]+x[3, 3] == 1.15*x[1, 0]+1.06*x[2, 3],
       x[4, 3] == 1.15*x[2, 0]+1.06*x[3, 3],
       x[2, 1]<=40000,x[1,2]<=30000]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优解为：', x.value)
print('最优值为：', prob.value)

例 4.4 捷运公司在下一年度的 1~4 月拟租用仓库堆放物资。已知各月所需仓库面积如表 4.2 所示，仓库租借费用随合同同期而定，期限越长，折扣越大。合同每月初均可办理，规定租用面积和期限。每次办理可签一份合同，也可签若干份租用面积和期限不同的合同，试确定该公司签订租借合同的最优决策，使所付租借费用最小。

表 4.2 所需仓库面积和租借仓库费用数据
月份 1 2 3 4
所需仓库面积 / 100 m^{2} 15 10 20 12
合同租借期限 / 月 1 2 3 4
合同期内的租费 / 元 2800 4500 6000 7300

建立线性规划模型

\text{min}z=2800\left(x_{11}+x_{21}+x_{31}+x_{41} \right )+4500\left(x_{12}+x_{22}+x_{32} \right )+6000\left(x_{13}+x_{23} \right )+7300x_{14} \\ \text{s.t.} \left\{\begin{matrix} x_{11}+x_{12}+x_{13}+x_{14} \geqslant15,\hfill \\ x_{12}+x_{13}+x_{14}+x_{21}+x_{22}+x_{23}\geqslant10,\\ x_{13}+x_{14}+x_{22}+x_{23}+x_{31}+x_{32}\geqslant10,\\ x_{14}+x_{23}+x_{32}+x_{41}\geqslant12,\hfill \\ x_{ij}\geqslant0,i=1,2,\cdots,4;\ j=1,2,\cdots,4. \end{matrix}\right.

# 程序文件 ex4_4.py
import cvxpy as cp
x = cp.Variable((4, 4), pos=True)
obj = cp.Minimize(2800*sum(x[:,0])+4500*sum(x[:3,1])+6000*sum(x[:2,2])+7300*x[0,3])
cons = [sum(x[1,:])>=15,
       sum(x[0,1:])+sum(x[2,:3])>=10,
       sum(x[0,2:])+sum(x[1,1:3])+sum(x[2,:2])>=20,
       x[0,3]+x[1,2]+x[2,1]+x[3,0]>=12]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优解为：\n',x.value)
print('最优值为：',prob.value)

例 4.5 计算 6 个产地 8 个销地的最小费用运输问题，单位商品运价如表 4.3 所示

表 4.3 单位商品运价表
B_{1} B_{2} B_{3} B_{4} B_{5} B_{6} B_{7} B_{8} 产量
A_{1} 6 4 6 7 4 2 5 9 60
A_{2} 4 9 5 3 8 5 8 2 55
A_{3} 5 2 1 9 7 4 3 3 51
A_{4} 7 6 7 3 9 2 7 1 43
A_{5} 2 3 9 5 7 2 6 5 41
A_{6} 5 5 2 2 8 1 4 3 52
销量 35 37 22 32 41 32 43 38

建立线性规划模型

\text{min}\sum\limits_{i=1}^{6}\sum\limits_{j=1}^{8}c_{ij}x_{ij}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{i=1}^{6}x_{ij}=d_{j},\ j=1,2,\cdots,8, \hfill \\ \sum\limits_{j=1}^{8}x_{ij} \leqslant e_{ij}, \ i=1,2,\cdots,6, \hfill \\ x_{ij} \geqslant0,\ i=1,2,\cdots,6; \ j=1,2,\cdots,8. \end{matrix}\right.

# 程序文件 ex4_5_1.py
import numpy as np
import cvxpy as cp
import pandas as pd
c = np.genfromtxt('data4_5_1.txt', dtype=float, max_rows=6, usecols=range(8)) # 读前 6 行前 8 列数据
e = np.genfromtxt('data4_5_1.txt', dtype=float, max_rows=6, usecols=8)        # 读最后一列数据
d = np.genfromtxt('data4_5_1.txt', dtype=float, skip_header=6)                # 读最后一行数据
x = cp.Variable((6, 8), pos=True)
obj = cp.Minimize(cp.sum(cp.multiply(c, x)))
con = [cp.sum(x,axis=0)==d,
      cp.sum(x,axis=1)<=e]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print('最优解为：\n', x.value)
print('最优值为：', prob.value)
xd = pd.DataFrame(x.value)
xd.to_excel('data4_5_2.xlsx')                                                 # 数据写到 excel 文件，便于做表使用

# 通过 excel 文件传递数据
# 程序文件 ex4_5_2.py
import cvxpy as cp
import pandas as pd
data = pd.read_excel('data4_5_3.xlsx', header=None)
data = data.values
c = data[:-1, :-1]
d = data[-1, :-1]
e = data[:-1, -1]
x = cp.Variable((6, 8), pos=True)
obj = cp.Minimize(cp.sum(cp.multiply(c, x)))
con = [cp.sum(x,axis=0)==d,
      cp.sum(x,axis=1)<=e]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print('最优解为：\n', x.value)
print('最优值为：', prob.value)
xd = pd.DataFrame(x.value)
xd.to_excel('data4_5_4.xlsx')

4.2 整数规划（Integer Programming，IP）

4.2.1 整数线性规划模型

 从决策变量的取值范围，可分为

（1）纯整数规划

（2）混合整数规划：决策变量一部分必须取整，另一部分可以不取整

（3）0-1整数规划：决策变量智能取 0 或 1。

\text{max}\left(or \ \text{min} \right )z=\sum\limits_{j=1}^{n}c_{j}x_{j}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{j=1}^{n}a_{ij}x_{j} \leqslant \left(or\ =,\geqslant \right)b_{i},\ i=1,2,\cdots,m, \\ x_{j} \geqslant0, \ j=1,2,\cdots,n, \hfill \\ x_{1},x_{2},\cdots,x_{n} \ \mbox{partial or full integer} . \hfill \end{matrix} \right.

例 4.6 背包问题

一个旅行者外出旅行，携带一背包，装一些最有用的东西，共有 n 件物品供选择。已知每件物品的“使用价值” c_{j} 和重量 a_{j}，要求

（1）最多携带物品的质量为 b\ \text{kg}。

（2）每件物品要么不带，要么只能整件携带。

这是决策问题中比较经典的 0-1 规划问题，要么带要么不带，是一个二值逻辑问题。

\text{max}z=\sum\limits_{i=1}^{n}c_{i}x_{i}, \\ \text{s.t.}\left\{\begin{matrix} \sum\limits_{i=1}^{n}a_{i}x_{i} \leqslant b, \hfill \\ x_{i}=0 \ or \ 1,\ i=1,2,\cdots,n. \end{matrix} \right.

例 4.7 指派问题

某单位有 n 项任务，正好需要 n 个人去完成，假设分配每个人只能完成一项任务。设 c_{ij} 表示分配第 i 个人去完成第 j 项任务的费用（时间等），问应如何指派，完成任务的总费用最小？

建立 0-1 整数规划模型：

\text{max}z=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n} c_{ij}x_{ij}, \\ \text{s.t.}\left\{\begin{matrix} \sum\limits_{j=1}^{n}x_{ij}=1, \ i=1,2,\cdots,n,\hfill \\ \sum\limits_{i=1}^{n}x_{ij}=1, \ j=1,2,\cdots,n,\hfill \\ x_{ij}=0 \ or \ 1,\ i,j=1,2,\cdots,n. \end{matrix} \right.

例 4.8 旅行商问题（货郎担问题）

有一推销员，从城市 v_{1} 出发，要遍历城市 v_{2},v_{3},\cdots,v_{n} 各一次，最后返回 v_{1} 。已知从 v_{i} 到  v_{j} 的旅费为 c_{ij}，试问应按怎样的次序访问这些城市，使得总旅费最少？

建立 0-1 整数规划模型：

\text{max}z=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n} c_{ij}x_{ij}, \\ \text{s.t.}\left\{\begin{matrix} \sum\limits_{i=1}^{n}x_{ij}=1, \ j=1,2,\cdots,n,\hfill \\ \sum\limits_{j=1}^{n}x_{ij}=1, \ i=1,2,\cdots,n,\hfill \\ u_{i}-u_{j}+nx_{ij} \leqslant n-1,\ i=1,\cdots,n,\ j=2,\cdots,n, \\ u_{1}=0,1 \leqslant u_{i} \leqslant n-1,\ i=2,3,\cdots,n, \hfill \\ x_{ij}=0 \ or \ 1,\ i,j=1,2,\cdots,n. \hfill \end{matrix} \right.

4.2.2 整数线性规划模型的求解

例 4.9 为了生产需要，某工厂的一条生产线需要每天 24h 不间断运转，但是每天不同时段所需要的工人最低数量不同，具体数据如表 4.5 所示。已知每名工人的连续工作时间为 8h。则该工厂应该为生产线配备多少名工人，才能保证生产线的正常运转？

表 4.5 工人数量需求表
班次 1 2 3 4 5 6
时间段 0:00-4:00 4:00-8:00 8:00-12:00 12:00-16:00 16:00-20:00 20:00-24:00
工人数量 35 40 50 45 55 30

\text{min}z=\sum\limits_{i=1}^{6}x_{i}, \\ \text{s.t.} \left \{ \begin{matrix} x_{1}+x_{6} \geqslant 35, \hfill \\ x_{1}+x_{2} \geqslant 40, \hfill \\ x_{2}+x_{3} \geqslant 50, \hfill \\ x_{3}+x_{4} \geqslant 45, \hfill \\ x_{4}+x_{5} \geqslant 55, \hfill \\ x_{5}+x_{6} \geqslant 30, \hfill \\ x_{i} \geqslant 0, \text{int},\ i=1,2,\cdots,6. \end{matrix} \right.

# 程序文件 e4_9_1.py
import cvxpy as cp
x = cp.Variable(6, integer=True)
obj = cp.Minimize(sum(x))
cons = [x[0]+x[5]>=35,x[0]+x[1]>=40,
       x[1]+x[2]>=50,x[2]+x[3]>=45,
       x[3]+x[4]>=55,x[4]+x[5]>=30,
       x>=0]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：', x.value)

# 求余运算
# 程序文件 ex4_9_2.py
import cvxpy as cp
import numpy as np
a = np.array([35, 40, 50, 45, 55, 30])
x = cp.Variable(6, integer=True)
obj = cp.Minimize(sum(x))
cons = [x>=0]
for i in range(6):
    cons.append(x[(i-1)%6]+x[i]>=a[i])
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：', x.value)

例 4.10 某连锁超市经营企业为了扩大规模，新租用 5 个门店，经过装修后再营业。现有 4 家装饰公司分别对 5 个门店的装修费用进行报价，具体数据如表 4.6 所列。为保证这些质量，规定每个装修公司最多承担两个店面的装修任务。为节省装修费用，该企业该如何分配装修任务？

表 4.6 装修费用表
门店 1 2 3 4 5
A 15 13.8 12.5 11 14.3
B 14.5 14 13.2 10.5 15
C 13.8 13 12.8 11.3 14.6
D 14.7 13.6 13 11.6 14

建立 0-1 整数规划模型：

\text{min}z=\sum\limits_{i=1}^{4}\sum\limits_{j=1}^{5}c_{ij}x_{ij}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{i=1}^{4}x_{ij}=1,\ j=1,2,\cdots,5, \hfill \\ \sum\limits_{j=1}^{5}x_{ij} \leqslant2, \ i=1,2,\cdots,4, \hfill \\ x_{ij}=0 \ or \ 1, \ i=1,2,\cdots,4,\ j=1,2,\cdots,5. \end{matrix} \right.

# 程序文件 ex4_10.py
import cvxpy as cp
import numpy as np
c = np.loadtxt('data4_10.txt')
x = cp.Variable((4, 5), integer=True)           # 定义决策变量
obj = cp.Minimize(cp.sum(cp.multiply(c, x)))    # 构造目标函数
cons = [0<=x, x<=1, cp.sum(x, axis=0)==1,       # 构造约束条件
        cp.sum(x, axis=1)<=2]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')                    # 求解问题
print('最优解为：\n', x.value)
print('最优值为：', prob.value)

例 4.11 已知 10 个商业网点的坐标如表 4.7 所列，现要在 10 个网点中选择适当位置设置供应站，要求供应站只能覆盖 10km 之内的网点，且每个供应站最多供应 5 个网点，如何设置才能使供应站的数目最小，并求最小供应站的个数。

表 4.7 商业网点 x 坐标和 y 坐标数据
x 9.4888 8.7928 11.5960 11.5643 5.6756 9.8497 9.1756 13.1385 15.4663 15.5464
y 5.6718 10.3868 3.9294 4.4325 9.9658 17.6632 6.1517 11.8569 8.8721 15.5868

建立 0-1 整数规划模型：

\text{min}\sum\limits_{i=1}^{10}x_{i}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{i=1}^{10}y_{ij} \geqslant 1,\ j=1,2,\cdots,10, \hfill \\ d_{ij}y_{ij} \leqslant 1,\ i,j=1,2,\cdots,10, \hfill \\ \sum\limits_{j=1}^{10}y_{ij} \leqslant 5,\ i=1,2,\cdots,10, \hfill \\ x_{i} \geqslant y_{ij}, \ i,j=1,2,\cdots,10, \hfill \\ x_{i}=y_{ii}, \ i=1,2,\cdots,10, \hfill \\ x_{i},y_{ji}=0\ or\ 1,\ i,j=1,2,\cdots,10. \end{matrix}\right.

# 程序文件 ex4_11.py
import cvxpy as cp
import numpy as np
a = np.loadtxt('data4_11.txt')
d = np.zeros((10, 10))
for i in range(10):
    for j in range(10):
        d[i, j] = np.linalg.norm(a[:, i]-a[:, j])
x = cp.Variable(10, integer=True)
y = cp.Variable((10, 10), integer=True)
obj = cp.Minimize(sum(x))
cons = [sum(y)>=1, cp.sum(y, axis=1)<=5,
        x>=0, x<=1, y>=0, y<=1]
for i in range(10):
    cons.append(x[i]==y[i, j])
    for j in range(10):
        cons.append(d[i, j]*y[i, j]<=10*x[i])
        cons.append(x[i]>=y[i, j])
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：\n', x.value)
print('----------\n', y.value)

4.3 投资的收益与风险

例 4.12 （选自 1998 年全国大学生数学建模竞赛 A 题）市场上有 n 种资产（如股票、债券、……）s_{i}\ \left(i=1,2,\cdots,n \right ) 供投资者选择，某公司有数额为 M 的一笔相当大的资金可用作一个时期的投资。公司财务分析人员对这 n 种 资产进行评估，估算出在这一时期内购买资产 s_{i} 的平均收益率为 r_{i}，并预测出购买 s_{i} 的风险损失率为 q_{i}。考虑到投资越分散，总的风险越小，公司确定，当用这笔资金购买若干种资产时，总体风险可用所投资的 s_{i} 中最大的一个风险来度量。

购买 s_{i} 要付交易费，费率为 p_{i}，并且当购买额不超过给定值 u_{i} 时，交易费按购买 u_{i} 计算（不买无须付费）。另外，假设同期银行存款利率是 r_{0}\left(r_{0}=5 \% \right )，且既无交易费又无风险。

已知 n=4 时的相关数据如表 4.8 所列。

表 4.8 4 种资产的相关数据
s_{i} r_{i}\ / \% q_{i}\ /\% p_{i}\ /\% u_{i}\ /元
s_{1} 28 2.5 1 103
s_{2} 21 1.5 2 198
s_{3} 23 5.5 4.5 52
s_{4} 25 2.6 6.5 40

试给该公司设计一种投资组合方案，即用给定的资金 M，有选择地购买若干种资产或存银行生息，使净收益尽可能大，而总体风险尽可能小。

模型一：固定风险水平，优化收益

\text{max} \sum\limits_{i=0}^{n} \left(r_{i}-p_{i} \right )x_{i}, \\ \text{s.t.}\left \{ \begin{matrix} \dfrac{q_{i}x_{i}}{M} \leqslant a, \ i=1,2,\cdots,n, \\ \sum\limits_{i=0}^{n} \left(1+p_{i} \right )x_{i}=M, \hfill \\ x_{i} \geqslant 0, \ i=0,1,\cdots,n. \hfill \end{matrix}\right.

模型二：固定盈利水平，极小化风险

\text{min} \left \{ \underset{1\leqslant i \leqslant n}{\text{max}} \left \{ q_{i}x_{i}\right \} \right \}, \\ \text{s.t.}\left \{ \begin{matrix} \sum\limits_{i=0}^{n} \left( r_{i}-p_{i} \right )x_{i} \geqslant kM, \hfill \\ \sum\limits_{i=0}^{n} \left(1+p_{i} \right )x_{i}=M, \hfill \\ x_{i} \geqslant 0, \ i=0,1,\cdots,n. \hfill \end{matrix}\right.

模型三：两个目标函数加权求和

\text{min} \ w\left \{ \underset{1 \leqslant i \leqslant n}{\text{max}} \left \{ q_{i}x_{i}\right \}\right \}-\left(1-w \right )\sum\limits_{i=0}^{n}\left(r_{i}-p_{i} \right )x_{i}, \\ \text{s.t.}\left \{ \begin{matrix} \sum\limits_{i=0}^{n} \left( 1+p_{i} \right )x_{i}=M, \hfill \\ x_{i} \geqslant 0, \ i=0,1,2,\cdots,n. \end{matrix} \right.

模型一求解

# 程序文件 ex4_12_1.py
import cvxpy as cp 
import pylab as plt

b = plt.array([0.025, 0.015, 0.055, 0.026])
c = plt.array([0.05, 0.27, 0.19, 0.185, 0.185])
x = cp.Variable(5, pos=True)
aeq = plt.array([1, 1.01, 1.02, 1.045, 1.065])
obj = cp.Maximize(c @ x)
a = 0; aa = []; Q = []; X = []; M = 10000;
while a < 0.05:
    con = [aeq @ x == M, cp.multiply(b, x[1:]) <= a*M]
    prob = cp.Problem(obj, con)
    prob.solve(solver='GLPK_MI')
    aa.append(a)
    Q.append(prob.value)
    X.append(x.value)
    a = a+0.001
plt.rc('text', usetex=True)
plt.rc('font', size=15)
plt.plot(aa, Q, 'r*')
plt.xlabel('$a$')
plt.ylabel('$Q$', rotation=0)
plt.show()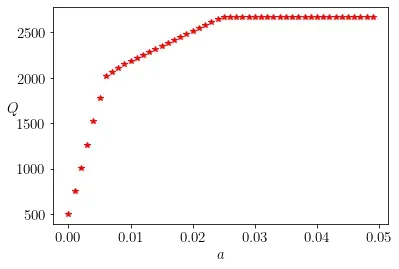

模型三求解

# 程序文件 ex4_12_2.py
import cvxpy as cp
import numpy as np
import pylab as plt

plt.rc('font', family='SimHei')
plt.rc('font', size=15)
x = cp.Variable(6, pos=True)
r = np.array([0.05, 0.28, 0.21, 0.23, 0.25])
p = np.array([0, 0.01, 0.02, 0.045, 0.065])
q = np.array([0, 0.025, 0.015, 0.055, 0.026])

def LP(w):
    V = []                # 风险初始化
    Q = []                # 收益初始化
    X = []                # 最优解的初始化
    con = [(1+p) @ x[:-1] == 10000, cp.multiply(q[1:], x[1:5]) <= x[5]]
    for i in range(len(w)):
        obj = cp.Minimize(w[i]*x[5]-(1-w[i])*((r-p) @ x[:-1]))
        prob = cp.Problem(obj, con)
        prob.solve(solver='GLPK_MI')
        xx = x.value      # 提出所有决策变量的取值
        V.append(max(q*xx[:-1]))
        Q.append((r-p) @ xx[:-1])
        X.append(xx)
    print('w=', w)
    print('V=', np.round(V, 2))
    print('Q=', np.round(Q, 2))
    plt.figure()
    plt.plot(V, Q, '*-')
    plt.grid('on')
    plt.xlabel('风险（元）')
    plt.ylabel('收益（元）')
    return X
    
w1 = np.arange(0, 1.1, 0.1)
LP(w1)
print('---------------')
w2 = np.array([0.766, 0.767, 0.810, 0.811, 0.824, 0.825, 0.962, 0.963, 1.0])
X = LP(w2)
print(X[-3])
plt.show()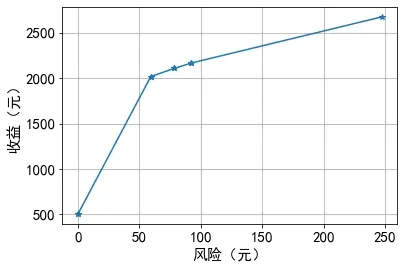

4.4 比赛项目排序问题

例 4.13 （选自 2005 年电工杯数学建模竞赛 B 题）

在各种运动比赛中，为了使比赛公平、公正、合理地举行，一个基本要求是：在比赛项目排序过程中，尽可能使每个运动员不连续参加两项比赛，以便运动员恢复体力，发挥正常水平。

表 4.11 所列为某个小型运动会的比赛报名表。有 14 个比赛项目，40 名运动员参加比赛。表中第 1 行表示 14 个比赛项目，第 1 列表示 40 名运动员，表中 “#” 位置表示运动员参加此项比赛。建立此问题的数学模型，要求合理安排比赛项目顺序，使连续参加两项比赛的运动员人次尽可能地少。

表 4.11 某小型运动会的比赛报名表
1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 # # # #
2 # # #
3 # # #
4 # # #
5 # # #
6 # #
7 # #
8 # #
9 # # # #
10 # # # #
11 # # # #
12 # #
13 # # #
14 # # #
15 # # #
16 # # #
17 # #
18 # #
19 # #
20 # #
21 # #
22 # #
23 # #
24 # # # #
25 # # #
26 # #
27 # #
28 # #
29 # # #
30 # #
31 # # #
32 # #
33 # #
34 # # # #
35 # # #
36 # #
37 # # #
38 # # # #
39 # # # #
40 # # # #

TSP 模型可表示为

\text{min}z=\sum\limits_{i=1}^{15}\sum\limits_{j=1}^{15}w_{ij}x_{ij}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{j=1}^{15}x_{ij}=1, \ i=1,2,\cdots,15, \hfill \\ \sum\limits_{i=1}^{15}x_{ij}=1, \ j=1,2,\cdots,15, \hfill \\ u_{i}-u_{j}+15x_{ij} \leqslant 14, \ i=1,2,\cdots,15,\ j=2,3,\cdots,15, \\ u_{1}=0, \ 1 \leqslant u_{i} \leqslant 14, \ i=2,3,\cdots,15, \hfill \\ x_{ij}=0 \ or \ 1, \ i,j=1,2,\cdots,15. \hfill \end{matrix} \right.

# 程序文件 ex4_13.py
import numpy as np
import pandas as pd
import cvxpy as cp

a = pd.read_excel("data4_13_1.xlsx", header=None)
a = a.values
a[np.isnan(a)]=0                             # 把空格对应的不确定值替换为0
m,n = a.shape
w = np.ones((n+1, n+1))*10000000             # 邻接矩阵初始化
for i in range(n):
    for j in range(n):
        if i != j:
            w[i, j] = sum(a[:, i]*a[:, j])
for i in range(n):
    w[i, n] = 0
    w[n, i] = 0
wd = pd.DataFrame(w)
wd.to_excel('data4_13_2.xlsx')               # 把邻接矩阵保存到 Excel 文件
x = cp.Variable((n+1, n+1), integer=True)
u = cp.Variable(n+1, integer=True)
obj = cp.Minimize(cp.sum(cp.multiply(w, x)))
con = [cp.sum(x, axis=0) == 1, cp.sum(x, axis=1) == 1,
      x>=0, x<=1, u[0]==0, u[1:]>=1, u[1:]<=n]
for i in range(n+1):
    for j in range(1, n+1):
        con.append(u[i]-u[j]+(n+1)*x[i, j]<=n)
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：\n', x.value)
i,j = np.nonzero(x.value)
print('xij=1对应的行列位置如下：')
print(i+1)
print(j+1)
最优值为： 2.0
最优解为：
 [[0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
xij=1对应的行列位置如下：
[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15]
[ 5 14  6  9 11  2  3  1  8 13  7 10 15 12  4]

TSP 回路为：15\rightarrow 4\rightarrow 9\rightarrow 8\rightarrow 1\rightarrow 5\rightarrow 11\rightarrow 7\rightarrow 3\rightarrow 6\rightarrow 2\rightarrow 14\rightarrow 12\rightarrow 10\rightarrow 13\rightarrow 15

版权声明：本文为博主作者：dezon原创文章，版权归属原作者，如果侵权，请联系我们删除！

原文链接：https://blog.csdn.net/dezon/article/details/133496778

共计人评分，平均分

到目前为止还没有投票！成为第一位评论此文章。

赞 (0)
xiaoxingxing的头像xiaoxingxing管理团队
0
上一篇 2024年4月16日
下一篇 2024年4月16日

相关推荐

此站出售，如需请站内私信或者邮箱！