1 研究背景
交替方向乘数法(ADMM)最初由Glowinski和Marrocco提出,用于解决非线性椭圆问题,它已成为解决各种凸优化问题的基准算法。在方法上,可以认为ADMM算法是在经典增广拉格朗日方法(ALM)的分裂版本。它已经在非常广泛的领域找到了应用,特别是在与数据科学相关的领域,如机器学习、计算机视觉和分布式/集中式优化。
(注:为什么将ADMM算法称为ALM的分裂版本)
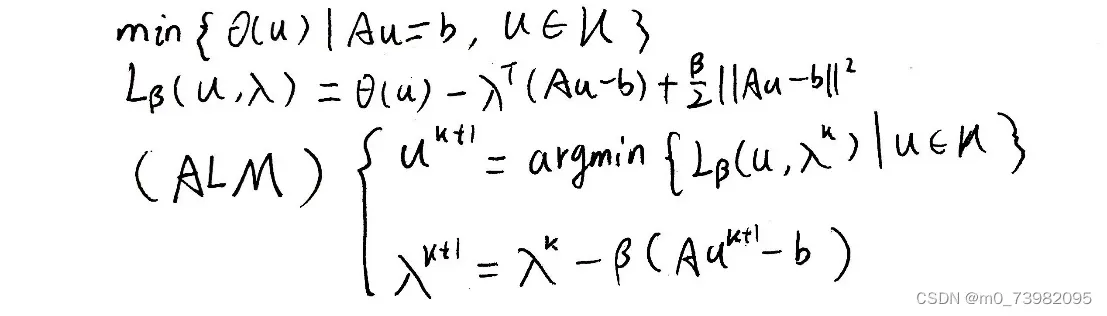
可以看出ALM可以解决一块的问题,而对于两块可分离凸优化问题ALM就比较困难,所以引入ADMM算法,可以说ADMM就是松弛的ALM,其中ADMM算法原型框架为:
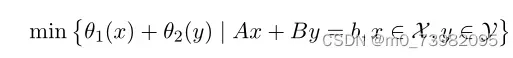
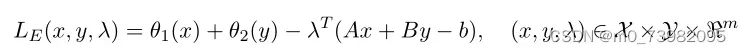
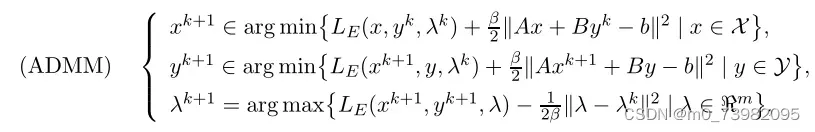
其中λk+1可以明确的写成:
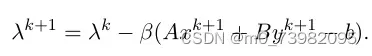
如果将两块可分离凸优化问题扩展到多块,可能会导致不收敛,故在本文中,如何将ADMM扩展到具有线性不等式约束的两块和多块(两块以上)可分离凸优化问题奠定了基础。
2 主要内容
2.1 收敛路线图
首先提出了一个统一的算法设计框架和一个在变分不等式背景下进行收敛分析的路线。
a、针对如下凸优化问题:
![]()
可以将它转换为变分不等式形式:
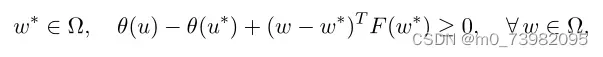
b、进一步的对几个符号做了定义:
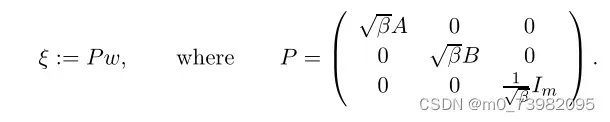
d、对证明收敛提出了统一框架:

针对这个统一框架可以分为两部分(预测和校正),故只需要凑出预测步骤找到花Q凑出校正步骤找到花M,有了这两个矩阵证明收敛就很容易了。
e、
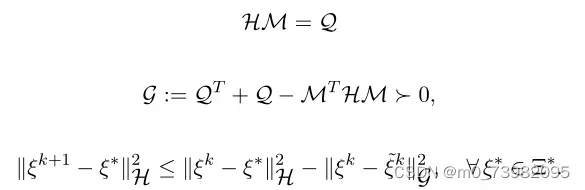
有了花Q和花M便有了H和G两个矩阵,我们已经证明了最后一个不等式是成立的,所以只要满足a中的P矩阵的条件就可以证明出所涉及的算法是收敛的。
在此基础上,可以设计一系列具体的基于ADMM的算法,这些算法在预测校正结构中具有可证明的收敛性。所提出的算法框架和收敛分析路线图适用于具有不同可分性程度的各种凸优化问题,其中可以包括线性等式和线性不等式约束。
2.2 原始ADMM的扩展
a、原始对偶扩展

其中第一步为预测步骤,利用预测步骤的值去更新迭代校正步骤。推导过程也很简单就是在原始ADMM算法的基础上去掉常数项演变而来,它的收敛性证明便遵循了上面所阐述的收敛性路线图,即先找到它的变分不等式然后凑出收敛性证明的预测校正框架即可。
b、更换迭代顺序

这个算法框架与原始的ADMM最主要的区别就是可以先进行λ的更新,收敛性证明同样遵循收敛性路线图以及收敛性框架。
2.3扩展到多块可分离凸优化问题
如果直接扩展到多块可能会不收敛,所以提出算法框架,并证明这个算法框架在处理多块的时候同样是收敛的,收敛性证明同样遵循上文提出的收敛路线及收敛统一框架。
a、原始扩展

同样是利用预测步骤的值在校正步骤中做更新迭代。
b、交换迭代顺序

这里就和前文对应了,主要是想说明作者在原始ADMM算法的基础上,所提出的新的算法框架是可行的也就是收敛的。
3 总结
本文建立了标准路线图,以证明所提出的原型算法框架在没有任何额外条件的情况下的收敛性。如果遵循路线图来推导从所提出的原型算法框架中指定的任何算法的收敛性,那么本质上它只需要指定两个矩阵,然后检查另一个矩阵的正定性。
目的就是从高层次和方法论的角度研究原始ADMM的扩展;因此本文没有给出任何实验结果。如前所述,所提出的原型算法框架基本上保持了原始ADMM(1.3)的所有主要结构和特征,这说明了它的通用性和效率,而额外的校正步骤在计算上非常简单。很容易从经验上验证从所提出的算法框架中指定的算法的效率。
这里就和前文对应了,主要是想说明作者在原始ADMM算法的基础上,所提出的新的算法框架是可行的也就是收敛的。
文章出处登录后可见!
