DFS：深搜+回溯+剪枝解决排列、子集问题

                                    创作不易，感谢三连支持！！ 

一、全排列I

. – 力扣（LeetCode）

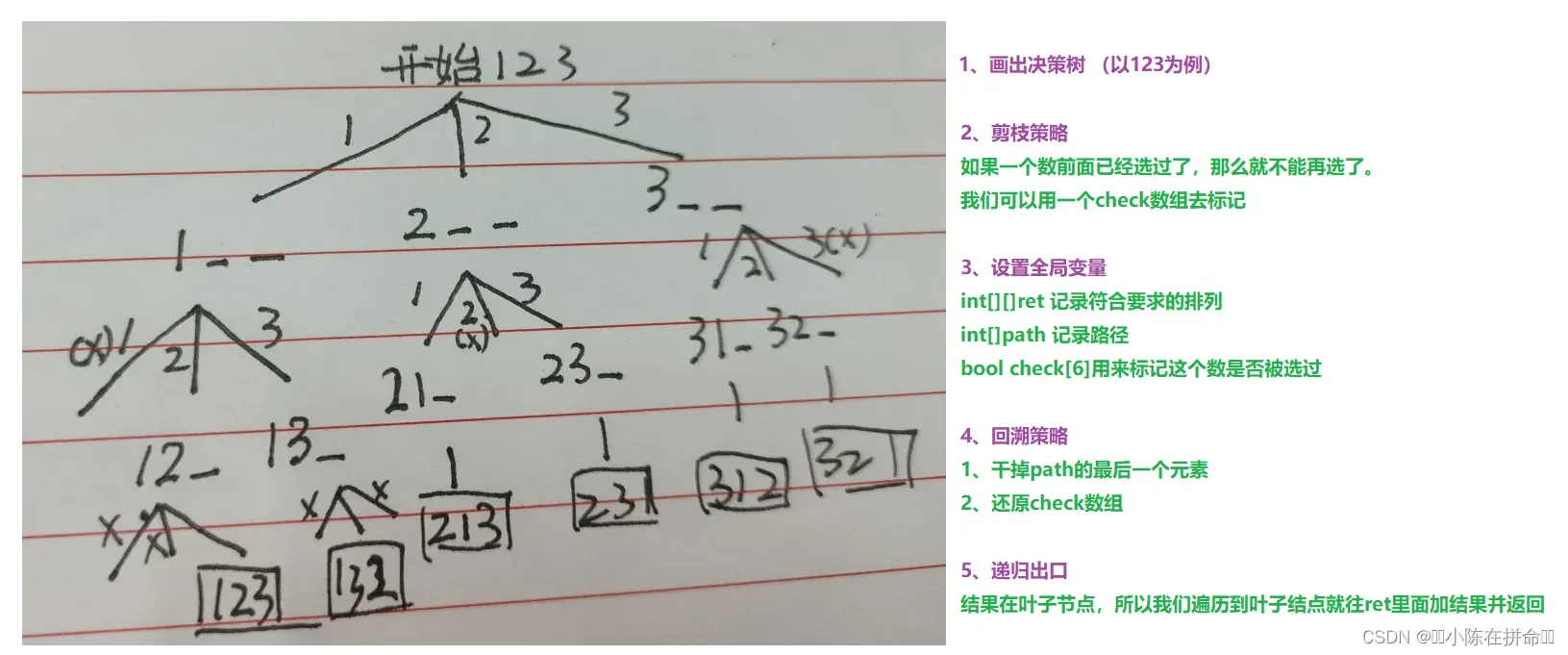
class Solution {
public:
    //全局变量
    vector<vector<int>> ret;
    vector<int> path;
    bool check[6];
    vector<vector<int>> permute(vector<int>& nums) 
    {
        dfs(nums);
        return ret;
    }

    void dfs(vector<int>& nums)
    {
        if(nums.size()==path.size()) {ret.push_back(path); return;}
        for(int i=0;i<nums.size();++i)
        {
            if(check[i]==false) //说明没选过
            {
                path.push_back(nums[i]);
                check[i]=true;//减枝
                dfs(nums);//继续去下一个找
                //回溯
                path.pop_back();
                check[i]=false;
            }
        }
    }
};

二、全排列II

. – 力扣（LeetCode）

 方案1：不合法就continue

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;
    bool check[8];
    vector<vector<int>> permuteUnique(vector<int>& nums) 
    {
       sort(nums.begin(),nums.end());
       dfs(nums);
       return ret;
    }

    void dfs(vector<int>& nums)
    {
        if(nums.size()==path.size()) {ret.push_back(path);return;}
        //思路1：考虑不合法的选择 continue   思路2：考虑合法的才进dfs
        for(int i=0;i<nums.size();++i)
        {
        if(check[i]==true||(i!=0&&nums[i]==nums[i-1]&&check[i-1]==false))  continue;
        path.push_back(nums[i]);
        check[i]=true;
        dfs(nums);//去下一层找
        path.pop_back();
        check[i]=false;
        }
    }
};

方案2：合法才能进循环

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;
    bool check[8];
    vector<vector<int>> permuteUnique(vector<int>& nums) 
    {
       sort(nums.begin(),nums.end());
       dfs(nums);
       return ret;
    }

    void dfs(vector<int>& nums)
    {
        if(nums.size()==path.size()) {ret.push_back(path);return;}
        //思路1：考虑不合法的选择 continue   思路2：考虑合法的才进dfs
        for(int i=0;i<nums.size();++i)
        {
        if(check[i]==false&&(i==0||nums[i]!=nums[i-1]||check[i-1]==true))  
        {
        path.push_back(nums[i]);
        check[i]=true;
        dfs(nums);//去下一层找
        path.pop_back();
        check[i]=false;
        }
        }
    }
};

三、优美的排列

. – 力扣（LeetCode）

class Solution {
public:  
    //类似全排列，可以交换位置但是不能重复
    int ret=0;
    bool check[16];
    int countArrangement(int n)
    {
       dfs(1,n);
       return ret;
    }

    void dfs(int pos,int n)
    {
        if(pos==n+1) {++ret;return;}
        for(int i=1;i<=n;++i)
        {
            if(check[i]==false&&(i%pos==0||pos%i==0))
            {
                 check[i]=true;
                 dfs(pos+1,n);
                 check[i]=false;
            }
        }
    }
};

四、子集I

. – 力扣（LeetCode）

 策略1：决策树以选不选作为参考，结果为叶子节点

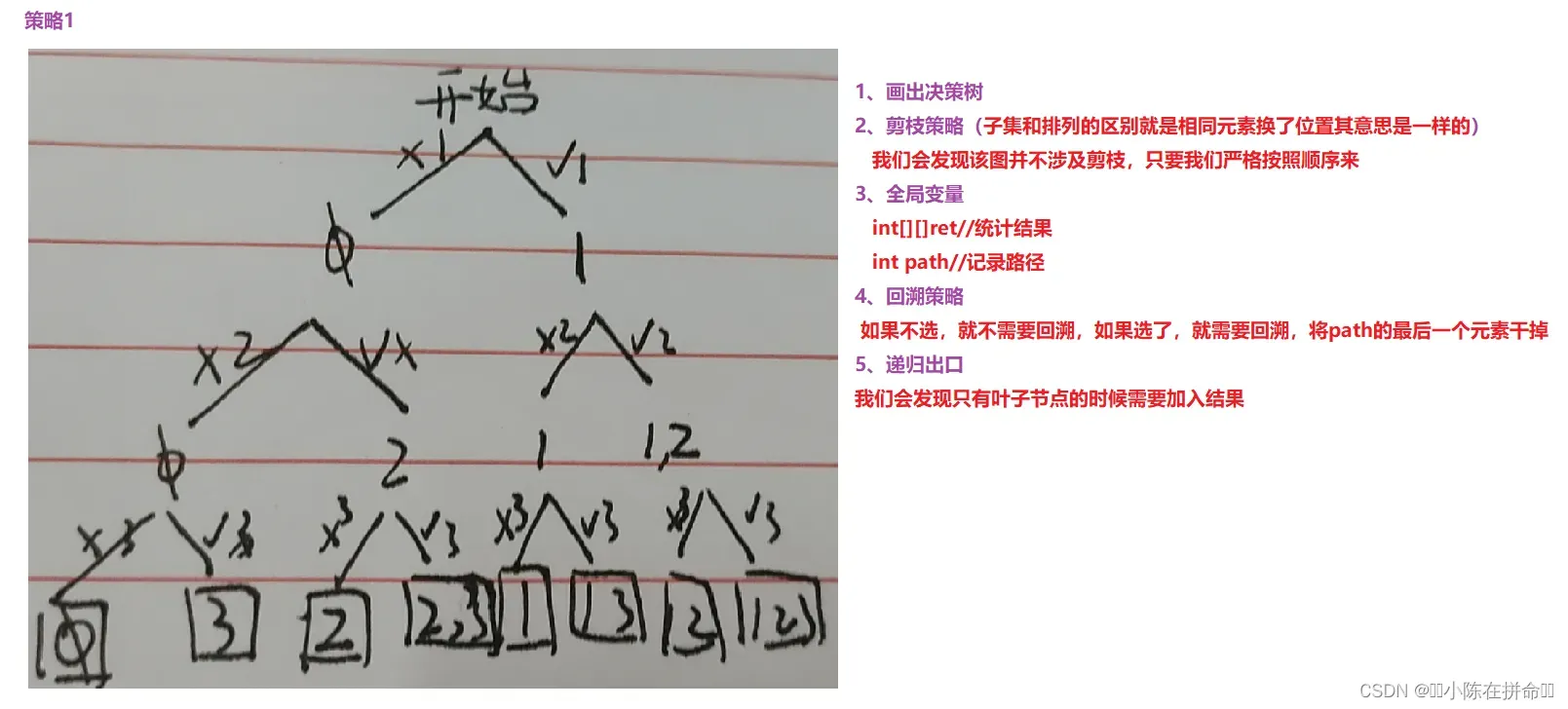
class Solution {
public:
    //设置全局变量
    vector<vector<int>> ret;
    vector<int> path;//记录路径
public:
    vector<vector<int>> subsets(vector<int>& nums) 
    {
        dfs(nums,0);
        return ret;
    }
    void dfs(vector<int>& nums,int pos)
    {
        if(pos==nums.size()) { ret.push_back(path);  return;}
        //选 
        path.push_back(nums[pos]);
        dfs(nums,pos+1);
        path.pop_back();//回溯
        //不选
        dfs(nums,pos+1);
    }
};

策略2：决策树以选几个为参考，结果为全部节点 

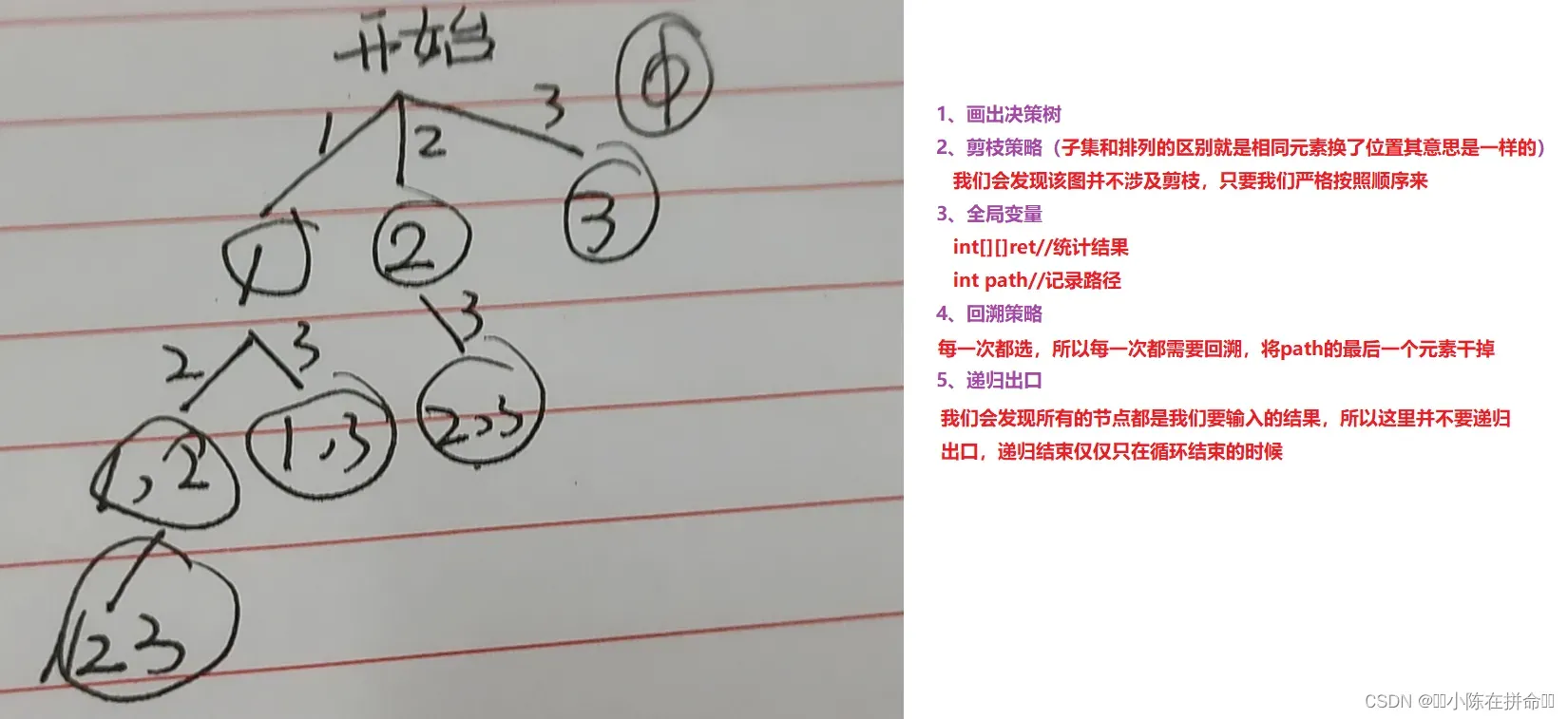
class Solution {
public:
    //设置全局变量
    vector<vector<int>> ret;
    vector<int> path;
public:
    vector<vector<int>> subsets(vector<int>& nums) 
    {
        dfs(nums,0);
        return ret;
    }
    void dfs(vector<int>& nums,int pos)
    {
        ret.push_back(path);//每一个决策都是结果
        for(int i=pos;i<nums.size();++i)
        {
            path.push_back(nums[i]);
            dfs(nums,i+1);   
            path.pop_back();         
        }
    }
};

五、子集II

. – 力扣（LeetCode）

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;
    vector<vector<int>> subsetsWithDup(vector<int>& nums) 
    {
       sort(nums.begin(), nums.end());
       dfs(nums,0);
       return ret;
    }

    void dfs(vector<int>& nums,int pos)
    {
        ret.push_back(path);
        for(int i=pos;i<nums.size();++i)
        {
                if(i>pos&&nums[i]==nums[i-1]) continue;
                path.push_back(nums[i]);
                dfs(nums,i+1);
                path.pop_back();
        }
    }
};

六、找出所有子集的异或总和再求和

. – 力扣（LeetCode）

class Solution {
    int sum=0;//记录总和
    int path=0;//记录路径
public:
    
    int subsetXORSum(vector<int>& nums) 
    {
      dfs(nums,0);
      return sum;
    }

    void dfs(vector<int>& nums,int pos)
    {
        sum+=path;
        for(int i=pos;i<nums.size();++i)
        {
            path^=nums[i];
            dfs(nums,i+1);
            path^=nums[i];//利用消消乐的性质恢复现场
        }
    }
};

七、字母大小写全排列

. – 力扣（LeetCode）

class Solution {
public:
    vector<string> ret; //找返回值
    vector<string> letterCasePermutation(string s) 
    {
       dfs(s,0);
       return ret;
    }

    void dfs(string s,int pos)//用传值s 可以直接在原来的s上进行修改
    {
        while(pos<s.size()&&isdigit(s[pos])) ++pos;
        if(pos==s.size()) {ret.push_back(s); return;}
        //变
        s[pos]^=32;  //^=32(空格)可以完成大小写转化！！
        dfs(s,pos+1);
        s[pos]^=32;
        //不变
        dfs(s,pos+1);
    }
};

八、下一个排列

. – 力扣（LeetCode）

class Solution {
public:
    void nextPermutation(vector<int>& nums) 
    {
        if(nums.size()==1) return;//如果只有一个数，就没有必要去修改了
      //思路，找尽可能靠右的低位，与一个尽可能小的大数交换 然后再升序后面的剩余元素
      for(int i=nums.size()-2;i>=0;--i)
      {
        if(nums[i]<nums[i+1]) 
        {
           for(int j=nums.size()-1;j>i;--j)
           {
            if(nums[i]<nums[j]) //找到第一个比i大，
            {
                swap(nums[i],nums[j]);
                sort(nums.begin()+i+1,nums.end());//i位置后面的数升序
                return;//此时返回结果
            }
           }
          }
      }
      //如果循环结束都没有找到第一个升序的，说明是全逆序，此时的结果应该是把你直接变成升序
      sort(nums.begin(),nums.end());
    }
};

九、排列序列

. – 力扣（LeetCode）​​​​​​

class Solution {
public:
    string getPermutation(int n, int k) 
    {
      vector<int> factorial(n);//用来统计各个阶乘
      factorial[0]=1;
      for(int i=1;i<n;++i)//统计1——（n-1）！的阶乘
      {
        factorial[i]= factorial[i-1]*i;
      }
      --k;//康托展开 
      vector<int> check(n+1,1);//可选数
      string ret;
      ret.reserve(n);
      for(int i=1;i<=n;++i)
      {
        int order=k/factorial[n-i]+1;//确定了康拖的首位
          for(int j=1;j<=n;++j)//告诉check数组，该位置得是0 不能再选
             {
                order-=check[j];
                if(order==0)
                {
                    ret.push_back(j+'0');
                    check[j]=0;//说明此数被选过
                    break;
                }
             }
             k%=factorial[n-i];//去找下一个数
      }
          return ret;
    }
};

     排列和子集问题就总结到这啦！！回溯有关的题关键就是画树状图，然后根据树状图去思考怎么进行深搜、回溯和剪枝！！