河马优化算法(Hippopotamus Optimization Algorithm,HO)是一种群智能优化算法,HO算法是从河马观察到的固有行为中汲取灵感而构思的,例如它们在河流或池塘中的位置更新,对捕食者的防御策略以及逃避捕食者的方法。该算法通过自适应地调整搜索空间的分辨率和搜索速度,以快速而准确地找到最优解,具有收敛速度快、求解精度高等特点,是一种不错的优化算法。该成果于2023年发表在知名SCI期刊、JCRQ1:Mathematics上。

HOA从河马生活中观察到的三种突出的行为模式中获得灵感,该模型结合了它们在河流或池塘中的位置更新、对捕食者的防御策略和逃避方法。
第一种行为模式:河马群由几只雌性河马、河马幼崽、多只成年雄性河马和一只占统治地位的雄性河马组成,由于它们天生的好奇心,幼河马和幼河马经常表现出离开群体的倾向。因此,它们可能会被孤立,成为捕食者的目标。
第二种行为模式是防御性的,当它们受到捕食者的攻击或其他生物侵入它们的领地时就会触发。狮子和斑点鬣狗等捕食者对这种现象有意识,并积极寻求避免直接暴露于河马可怕的下颚,作为预防潜在伤害的预防措施。
最后一种行为模式包含了河马逃离捕食者的本能反应,并积极寻求远离潜在危险的区域。在这种情况下,河马会努力向最近的水体航行,比如河流或池塘,因为狮子和斑点鬣狗经常表现出对进入水生环境的厌恶。

1、算法原理
(1)初始化
HO是一种基于种群的优化算法,其中搜索代理是随机的。在HO算法中,河马是优化问题的候选解,这意味着每个河马在搜索空间中的位置更新表示决策变量的值。类似于传统的优化算法,HO的初始化阶段涉及随机初始解的生成。在此步骤中,使用以下公式生成决策变量的向量:
其中,表示第个候选解的位置,是0到1范围内的随机数,并且和分别表示第个决策变量的下限和上限。其中表示兽群中河马的种群大小,表示问题中决策变量的个数,种群矩阵由式(2)表示。
(2)河马在河流或池塘中的位置更新
河马群由几只成年雌性河马、小河马、多只成年雄性河马和占统治地位的雄性河马组成。根据目标函数值迭代确定优势河马(最小化问题最低,最大化问题最高)。通常,河马倾向于彼此靠近地聚集在一起。占统治地位的雄性河马保护兽群和领地免受潜在威胁。多只雌性河马被安置在雄性河马周围。成年后,雄性河马会被占统治地位的雄性赶出兽群。这些被驱逐的雄性个体被要求吸引雌性或与其他已建立的雄性成员进行统治竞争,以建立自己的统治地位。下式表示了群体中雄性河马成员在湖泊或池塘中的位置的数学表示。
在式中,表示雄性河马的位置,表示优势河马的位置(即当前迭代中成本最优的河马)。
如果t大于0.6,则表明未成熟的河马已经远离母河马,下式描述了雄性和雌性或未成熟河马在群体中的位置更新。F为目标函数值。
МКірроВпірроВћіррое
在第二种行为中,通过使用h向量、I1和l2场景增强了HO算法的全局搜索,提高了算法的探索能力。该算法具有较好的全局搜索性能,提高了算法的搜索速度。
(3)河马防御捕食者(探索阶段)
河马采用的主要防御策略是迅速转向捕食者,并发出响亮的叫声,以阻止捕食者靠近它们。在这个阶段,河马可能会表现出接近捕食者的行为,以诱导其撤退,从而有效地抵御潜在的威胁。下式表示捕食者在搜索空间中的位置。
其中表示一个从0到1的随机向量。
该式表示第i只河马到捕食者的距离。在此期间,河马采取了一种基于捕食者因素的防御行为,以保护自己免受捕食者的侵害。如果predator小于F,表明捕食者离河马非常近,在这种情况下,河马迅速转向捕食者,并向它移动,使它撤退。predator越大,表示捕食者或入侵实体处于较大状态。
由以下公式可知,如果某只河马已被猎取,则说明该河马已被猎取,将会有另一只河马在群中取代它,否则猎取者逃跑,该河马将返回群中。在第二阶段,在全局搜索过程中观察到显著的增强。第一阶段和第二阶段相辅相成,有效地降低了陷入局部最小值的风险。
(4)河马逃离捕食者(剥削阶段)
未成熟的河马,甚至是成年的河马,如果与兽群分离,面对一群狮子或斑点鬣狗,都很容易受到捕食者的攻击。在这种情况下,河马试图离开该区域。通常,河马试图跑到最近的湖泊或池塘,以避免捕食者的伤害,因为斑点狮子和鬣狗避免进入湖泊或池塘。这种策略导致河马在当前位置附近找到一个安全的位置,并在HO的第三阶段模拟这种行为,从而增强了在局部搜索中的开发能力。这种策略导致河马找到一个靠近当前位置的安全位置,并在HO的第三阶段模拟这种行为,从而增强了利用局部搜索的能力。为了模拟这种行为,在河马当前位置附近生成一个随机位置。
根据下式对河马的这种行为进行建模。当新创建的位置提高了成本函数值时,表明河马在当前位置附近找到了一个更安全的位置,并相应地改变了自己的位置。t表示当前迭代。
在式中,是为寻找最近的安全地点而搜索河马的位置.
在该式中,表示0到1之间的随机向量,表示生成的随机数,取值范围为0~1,另外,是正态分布的随机数。
2、结果展示
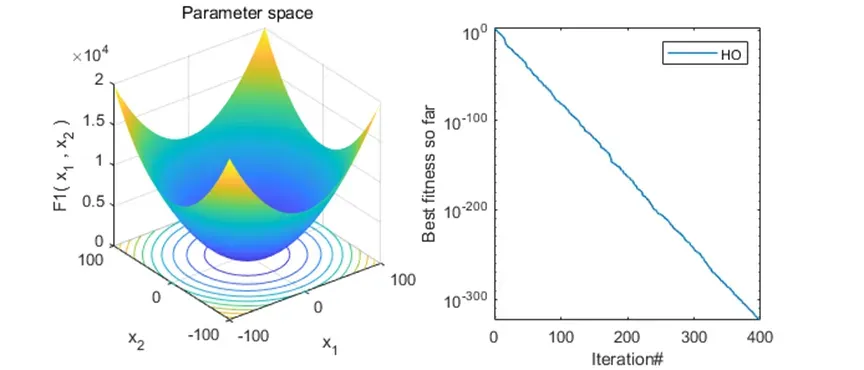
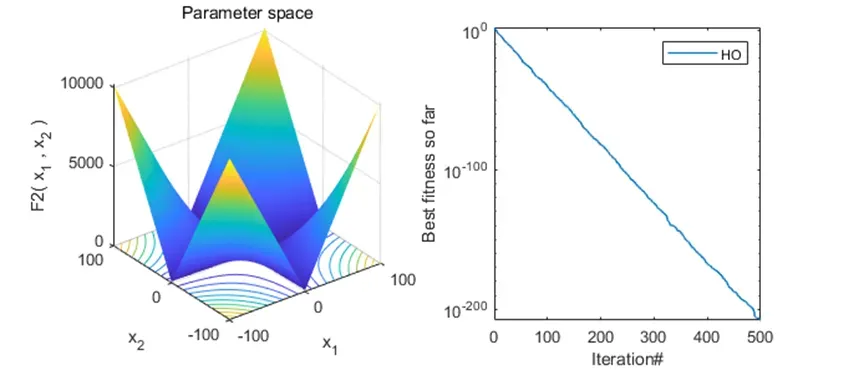
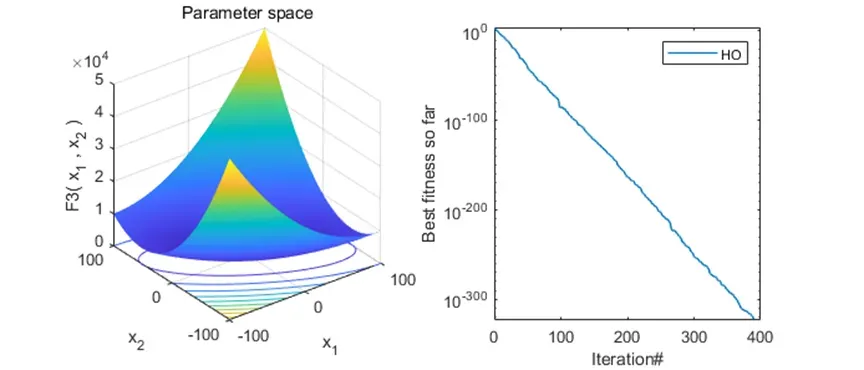
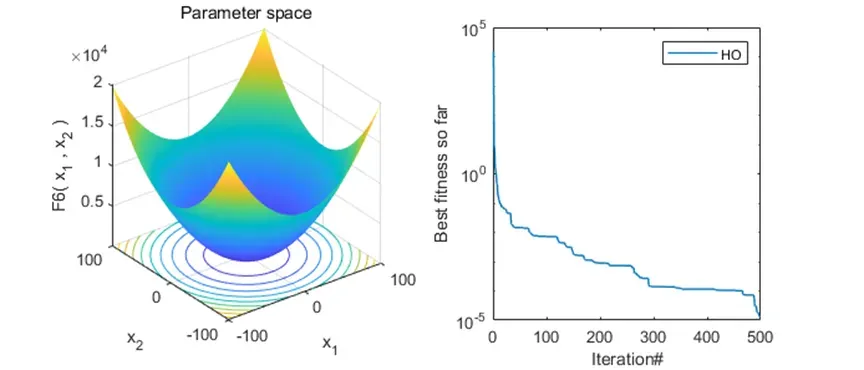
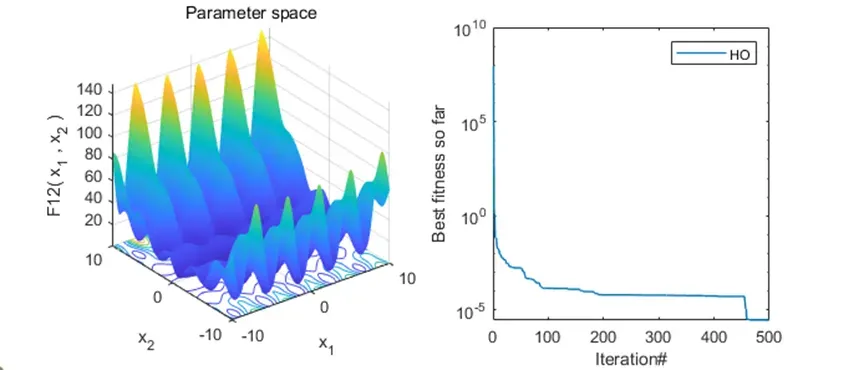
可以看到,该算法基本不会陷入局部最优解。搜索效率也还不错!
3、MATLAB核心代码
%% 淘个代码 %%
% 微信公众号搜索:淘个代码,获取更多代码
% 河马优化算法(HOA)
%% Designed and Developed by Mohammad Hussien Amiri and Nastaran Mehrabi Hashjin
function[Best_score,Best_pos,HO_curve]=HO(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness)
lowerbound=ones(1,dimension).*(lowerbound); % Lower limit for variables
upperbound=ones(1,dimension).*(upperbound); % Upper limit for variables
%% Initialization
for i=1:dimension
X(:,i) = lowerbound(i)+rand(SearchAgents,1).*(upperbound(i) - lowerbound(i)); % Initial population
end
for i =1:SearchAgents
L=X(i,:);
fit(i)=fitness(L);
end
%% Main Loop
for t=1:Max_iterations
%% Update the Best Condidate Solution
[best , location]=min(fit);
if t==1
Xbest=X(location,:); % Optimal location
fbest=best; % The optimization objective function
elseif best<fbest
fbest=best;
Xbest=X(location,:);
end
for i=1:SearchAgents/2
%% Phase1: The hippopotamuses position update in the river or pond (Exploration)
Dominant_hippopotamus=Xbest;
I1=randi([1,2],1,1);
I2=randi([1,2],1,1);
Ip1=randi([0,1],1,2);
RandGroupNumber=randperm(SearchAgents,1);
RandGroup=randperm(SearchAgents,RandGroupNumber);
% Mean of Random Group
MeanGroup=mean(X(RandGroup,:)).*(length(RandGroup)~=1)+X(RandGroup(1,1),:)*(length(RandGroup)==1);
Alfa{1,:}=(I2*rand(1,dimension)+(~Ip1(1)));
Alfa{2,:}= 2*rand(1,dimension)-1;
Alfa{3,:}= rand(1,dimension);
Alfa{4,:}= (I1*rand(1,dimension)+(~Ip1(2)));
Alfa{5,:}=rand;
A=Alfa{randi([1,5],1,1),:};
B=Alfa{randi([1,5],1,1),:};
X_P1(i,:)=X(i,:)+rand(1,1).*(Dominant_hippopotamus-I1.*X(i,:));
T=exp(-t/Max_iterations);
if T>0.6
X_P2(i,:)=X(i,:)+A.*(Dominant_hippopotamus-I2.*MeanGroup);
else
if rand()>0.5
X_P2(i,:)=X(i,:)+B.*(MeanGroup-Dominant_hippopotamus);
else
X_P2(i,:)=((upperbound-lowerbound)*rand+lowerbound);
end
end
X_P2(i,:) = min(max(X_P2(i,:),lowerbound),upperbound);
L=X_P1(i,:);
F_P1(i)=fitness(L);
if(F_P1(i)<fit(i))
X(i,:) = X_P1(i,:);
fit(i) = F_P1(i);
end
L2=X_P2(i,:);
F_P2(i)=fitness(L2);
if(F_P2(i)<fit(i))
X(i,:) = X_P2(i,:);
fit(i) = F_P2(i);
end
end
%% Phase 2: Hippopotamus defense against predators (Exploration)
for i=1+SearchAgents/2 :SearchAgents
predator=lowerbound+rand(1,dimension).*(upperbound-lowerbound);
L=predator;
F_HL=fitness(L);
distance2Leader=abs(predator-X(i,:));
b=unifrnd(2,4,[1 1]);
c=unifrnd(1,1.5,[1 1]);
d=unifrnd(2,3,[1 1]);
l=unifrnd(-2*pi,2*pi,[1 1]);
RL=0.05*levy(SearchAgents,dimension,1.5);
if fit(i)> F_HL
X_P3(i,:)=RL(i,:).*predator+(b./(c-d*cos(l))).*(1./distance2Leader);
else
X_P3(i,:)=RL(i,:).*predator+(b./(c-d*cos(l))).*(1./(2.*distance2Leader+rand(1,dimension)));
end
X_P3(i,:) = min(max(X_P3(i,:),lowerbound),upperbound);
L=X_P3(i,:);
F_P3(i)=fitness(L);
if(F_P3(i)<fit(i))
X(i,:) = X_P3(i,:);
fit(i) = F_P3(i);
end
end
%% Phase 3: Hippopotamus Escaping from the Predator (Exploitation)
for i=1:SearchAgents
LO_LOCAL=(lowerbound./t);
HI_LOCAL=(upperbound./t);
Alfa{1,:}= 2*rand(1,dimension)-1;
Alfa{2,:}= rand(1,1);
Alfa{3,:}=randn;
D=Alfa{randi([1,3],1,1),:};
X_P4(i,:)=X(i,:)+(rand(1,1)).*(LO_LOCAL+D.* (HI_LOCAL-LO_LOCAL));
X_P4(i,:) = min(max(X_P4(i,:),lowerbound),upperbound);
L=X_P4(i,:);
F_P4(i)=fitness(L);
if(F_P4(i)<fit(i))
X(i,:) = X_P4(i,:);
fit(i) = F_P4(i);
end
end
best_so_far(t)=fbest;
disp(['Iteration ' num2str(t) ': Best Cost = ' num2str(best_so_far(t))]);
Best_score=fbest;
Best_pos=Xbest;
HO_curve=best_so_far;
end
end参考文献
[1] Amiri M H, Hash** N M, Montazeri M, et al. Hippopotamus Optimization Algorithm: A Novel Nature-Inspired Optimization Algorithm[J]. 2023.
完整代码获取方式:后台回复关键字:
TGDM199
版权声明:本文为博主作者:今天吃饺子原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/woaipythonmeme/article/details/136385522
