概述:
什么是数学规划?
数学建模中的数学规划是指利用数学方法和技巧对问题进行数学建模,并通过数学规划模型求解最优解的过程。数学规划是一种数学优化方法,旨在找到使目标函数达到最大值或最小值的变量取值,同时满足一系列约束条件。
数学规划包括多种不同类型的问题,其中最常见的包括线性规划(Linear Programming)、整数规划(Integer Programming)、非线性规划(Nonlinear Programming)、混合整数规划(Mixed Integer Programming)等。
线性规划在前面的回答中已经介绍过,它适用于目标函数和约束条件均为线性的情况。
整数规划是线性规划的扩展,其中决策变量被限制为整数取值。这种问题常见于在决策中需要选择整数数量或整数类型的情况,如装载问题、制定生产计划等。
非线性规划则涉及目标函数和/或约束条件含有非线性项的情况。此类问题的求解相对复杂,通常需要使用迭代和数值优化算法,如牛顿法、拟牛顿法等。
混合整数规划结合了整数规划和非线性规划的特点,既包含整数变量,又涉及非线性项。这种问题在实际应用中广泛存在,例如运输路线优化、设备安排等。
数学规划的求解方法包括传统的数值优化算法(如单纯形法、分支定界法)和近年来发展起来的启发式算法(如遗传算法、模拟退火算法)。通过结合不同的约束条件和求解算法,可以针对特定问题选择最合适的数学规划方法。
总之,数学规划是数学建模中重要的工具,通过建立适当的数学模型,可以解决各种实际问题,并为决策提供科学依据。
数学规划的一般形式:
数学规划的一般形式可以表示为如下的数学模型:
最小化(或最大化)目标函数:
[ f(x) ]
在给定约束条件下,求解决策变量 ( x ) 的最优解。这里的决策变量可以是一个向量或者一组变量。
约束条件包括等式约束和不等式约束,可以表示为:
等式约束:
[ g_i(x) = 0, \quad i = 1, 2, \ldots, m ]
不等式约束:
[ h_j(x) \leq 0, \quad j = 1, 2, \ldots, n ]
其中, ( gi(x) ) 和 ( hj(x) ) 分别表示等式约束和不等式约束的函数,它们与决策变量 ( x ) 有关。
一般情况下,还需要给定决策变量 ( x ) 的取值范围(上下界约束):
[ x{\text{min}} \leq x \leq x{\text{max}} ]
最优解满足所有约束条件,并且使目标函数取得最小(或最大)值。
数学规划的具体形式会根据具体问题的特点而有所不同。常见的数学规划模型包括线性规划(LP)、整数规划(IP)、非线性规划(NLP)、混合整数规划(MIP)等。
在数学规划中,通常会使用数值优化算法来求解最优解,这些算法包括线性规划的单纯形法、内点法,以及非线性规划的牛顿法、拟牛顿法等。近年来,启发式算法如遗传算法、粒子群优化等也在数学规划中得到广泛应用。
数学规划的分类:
数学规划可以根据问题的特性进行不同的分类。以下是常见的数学规划分类:
1.线性规划(Linear Programming, LP):目标函数和约束条件均为线性的规划问题。决策变量的取值可以是实数。线性规划是最早和最经典的数学规划问题之一。
2.整数规划(Integer Programming, IP):线性规划的扩展,决策变量被限制为整数取值。这种问题常见于需要选择整数数量或整数类型的场景,如装载问题、制定生产计划等。
3.非线性规划(Nonlinear Programming, NLP):目标函数和/或约束条件具有非线性项的规划问题。这种问题的数学模型更复杂,通常需要使用迭代和数值优化算法来求解,如牛顿法、拟牛顿法等。
4.0-1规划(0-1 Programming):整数规划的特列,整数变量的取值只能为0和1。
线性规划问题的求解
- matlab中线性规划的标准型

- matlab求解线性规划的命令
函数linprog()
接收值:
X:目标函数中x1,x2……xm的求解值
Fval:目标函数求取最小值的值
参数值:
C:目标函数的系数
A:不等式约束的系数
b:不等式约束的常数项
Aeq:等式约束的系数
Beq:等式约束的常数项
Lb:目标函数中自变量x1……xm的下限
Ub:目标函数中自变量x1……xm的上限
X0:初始值(在一些规划中可以不添加)
线性规划练习题:
在求解过程中需要将系数/常数的向量转置成如下列例题中列好的列向量,方法在定义好的行向量后加’:[]’
规划函数只能求最小值,若题目中有最大值或>=的不等式约束要在对应的式子中添加负号变为min/<=。其余式子不变。
参考代码:
%% Matlab求解线性规划
% [x fval] = linprog(c, A, b, Aeq, beq, lb,ub, x0)
% c是目标函数的系数向量,A是不等式约束Ax<=b的系数矩阵,b是不等式约束Ax<=b的常数项
% Aeq是等式约束Aeq x=beq的系数矩阵,beq是等式约束Aeq x=beq的常数项
% lb是X的下限,ub是X的上限,X是向量[x1,x2,...xn]' , 即决策变量。
% 迭代的初始值为x0(一般不用给)
% 更多该函数的用法说明请看讲义
%% 例题1
c = [-5 -4 -6]'; % 加单引号表示转置
% c = [-5 -4 -6]; % 写成行向量也是可以的,不过不推荐,我们按照标准型来写看起来比较正规
A = [1 -1 1;
3 2 4;
3 2 0];
b = [20 42 30]';
lb = [0 0 0]';
[x fval] = linprog(c, A, b, [], [], lb) % ub我们直接不写,则意味着没有上界的约束
% x =
% 0
% 15.0000
% 3.0000
%
% fval =
% -78
%% 例题2
c = [0.04 0.15 0.1 0.125]';
A = [-0.03 -0.3 0 -0.15;
0.14 0 0 0.07];
b = [-32 42]';
Aeq = [0.05 0 0.2 0.1];
beq = 24;
lb = [0 0 0 0]';
[x fval] = linprog(c, A, b, Aeq, beq, lb)
% x =
% 0
% 106.6667
% 120.0000
% 0
%
% fval =
% 28
% 这个题可能有多个解,即有多个x可以使得目标函数的最小值为28(不同的Matlab版本可能得到的x的值不同,但最后的最小值一定是28)
% 例如我们更改一个限定条件:令x1要大于0(注意Matlab中线性规划的标准型要求的不等式约束的符号是小于等于0)
% x1 >0 等价于 -x1 < 0,那么给定 -x1 <= -0.1 (根据实际问题可以给一个略小于0的数-0.1),这样能将小于号转换为小于等于号,满足Matlab的标准型
c = [0.04 0.15 0.1 0.125]';
A = [-0.03 -0.3 0 -0.15;
0.14 0 0 0.07
-1 0 0 0];
b = [-32 42 -0.1]';
Aeq = [0.05 0 0.2 0.1];
beq = 24;
lb = [0 0 0 0]';
[x fval] = linprog(c, A, b, Aeq, beq, lb)
% x =
% 0.1000
% 106.6567
% 119.9750
% 0
%
% fval =
% 28.0000
%% 例题3
c = [-2 -3 5]';
A = [-2 5 -1;
1 3 1];
b = [-10 12];
Aeq = ones(1,3);
beq = 7;
lb = zeros(3,1);
[x fval] = linprog(c, A, b, Aeq, beq, lb)
fval = -fval % 注意这个fval要取负号(原来是求最大值,我们添加负号变成了最小值问题)
% x =
% 6.4286
% 0.5714
% 0
% fval =
% -14.5714
% fval =
% 14.5714
%% 多个解的情况
% 例如 : min z = x1 + x2 s.t. x1 + x2 >= 10
c = [1 1]';
A = [-1 -1];
b = -10;
[x fval] = linprog(c, A, b) % Aeq, beq, lb和ub我们都没写,意味着没有等式约束和上下界约束
% x有多个解时,Matlab会给我们返回其中的一个解
%% 不存在解的情况
% 例如 : min z = x1 + x2 s.t. x1 + x2 = 10 、 x1 + 2*x2 <= 8、 x1 >=0 ,x2 >=0
c = [1 1]';
A = [1 2];
b = 8;
Aeq = [1 1];
beq = 10;
lb = [0 0]';
[x fval] = linprog(c, A, b, Aeq, beq, lb) % Linprog stopped because no point satisfies the constraints.(没有任何一个点满足约束条件)整数规划:
整数规划(Integer Programming, IP)是一种数学规划方法,其中决策变量被限制为整数值。整数规划是线性规划的扩展,旨在解决需要在整数取值范围内做出决策的问题。
整数规划的一般形式可以表示为:
最小化(或最大化)目标函数:
[ f(x) ]
在给定约束条件下,求解决策变量 ( x ) 的最优整数解。
约束条件包括等式约束和不等式约束,可以表示为:
等式约束:
[ g_i(x) = 0, \quad i = 1, 2, \ldots, m ]
不等式约束:
[ h_j(x) \leq 0, \quad j = 1, 2, \ldots, n ]
其中, ( gi(x) ) 和 ( hj(x) ) 为函数,与决策变量 ( x ) 有关。
整数规划问题在实际应用中非常常见,因为存在许多情况下必须做出离散(整数)决策的需要。例如,装载问题中需要决定将货物装在哪辆卡车上;制定生产计划时需要决定生产数量;旅行商问题中需要选择访问的城市顺序等。
整数规划的求解方法相较于线性规划更为困难,因为整数域的离散性质增加了问题的复杂性。常见的整数规划求解方法包括分支定界法(Branch and Bound)、割平面法(Cutting Plane)、启发式算法(Heuristic Algorithms)等。
在实际问题中,常常需要将问题转化为整数规划模型,并利用整数规划方法求解最优解。整数规划的应用广泛,涵盖了物流、生产管理、航空航天、金融投资等众多领域。
Matlzb中的操作:
与线性规划操作相比添加一项整数向量,在约束条件中目标函数中那个自变量xn是整数就将他的下标写在intcon中。


代码参考:
%% 线性整数规划问题
%% 例1
c=[-20,-10]';
intcon=[1,2]; % x1和x2限定为整数
A=[5,4;
2,5];
b=[24;13];
lb=zeros(2,1);
[x,fval]=intlinprog(c,intcon,A,b,[],[],lb)
fval = -fval
%% 例2
c=[18,23,5]';
intcon=3; % x3限定为整数
A=[107,500,0;
72,121,65;
-107,-500,0;
-72,-121,-65];
b=[50000;2250;-500;-2000];
lb=zeros(3,1);
[x,fval]=intlinprog(c,intcon,A,b,[],[],lb)
%% 例3
c=[-3;-2;-1]; intcon=3; % x3限定为整数
A=ones(1,3); b=7;
Aeq=[4 2 1]; beq=12;
lb=zeros(3,1); ub=[+inf;+inf;1]; %x(3)为0-1变量
[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)0-1规划经典例题:
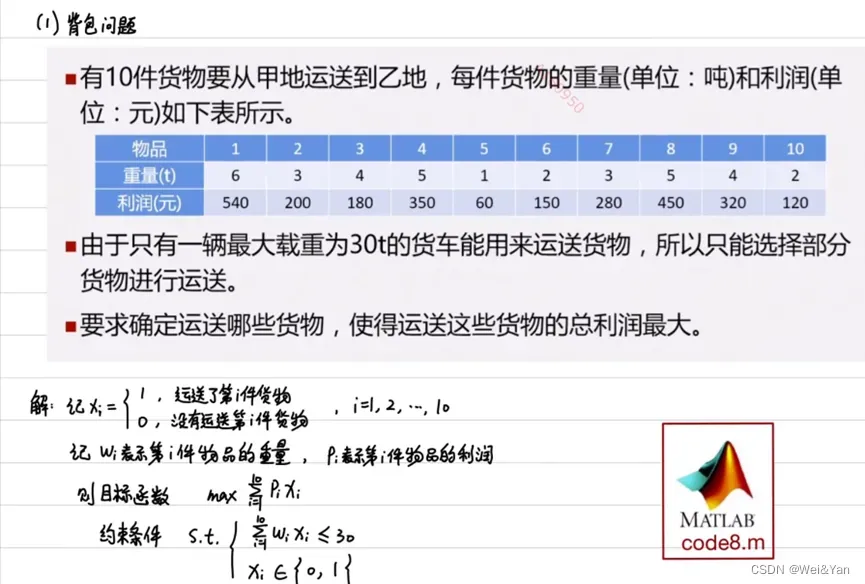
背包问题:
指派问题: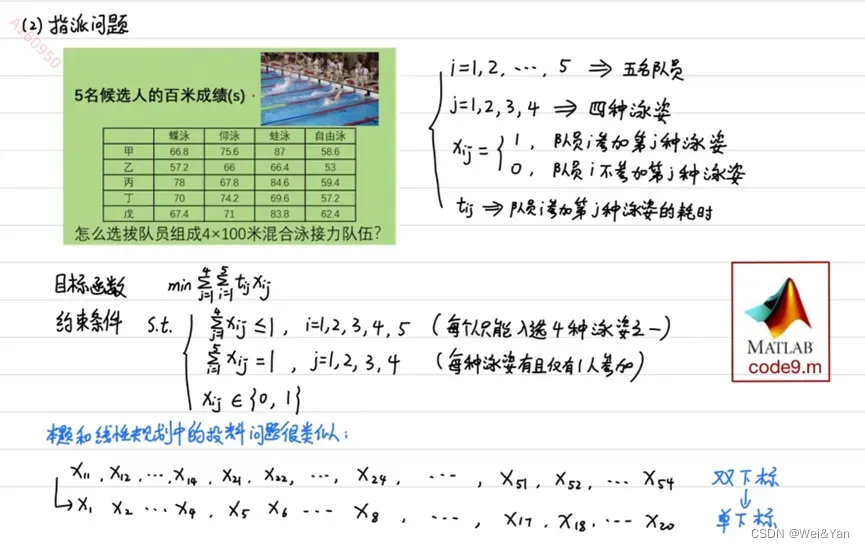
参考代码:
背包问题:
%% 背包问题(货车运送货物的问题)
c = -[540 200 180 350 60 150 280 450 320 120]; % 目标函数的系数矩阵(最大化问题记得加负号)
intcon=[1:10]; % 整数变量的位置(一共10个决策变量,均为0-1整数变量)
A = [6 3 4 5 1 2 3 5 4 2]; b = 30; % 线性不等式约束的系数矩阵和常数项向量(物品的重量不能超过30)
Aeq = []; beq =[]; % 不存在线性等式约束
lb = zeros(10,1); % 约束变量的范围下限
ub = ones(10,1); % 约束变量的范围上限
%最后调用intlinprog()函数
[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
fval = -fval
%% 指派问题(选择队员去进行游泳接力比赛)
clear;clc
c = [66.8 75.6 87 58.6 57.2 66 66.4 53 78 67.8 84.6 59.4 70 74.2 69.6 57.2 67.4 71 83.8 62.4]'; % 目标函数的系数矩阵(先列后行的写法)
intcon = [1:20]; % 整数变量的位置(一共20个决策变量,均为0-1整数变量)
% 线性不等式约束的系数矩阵和常数项向量(每个人只能入选四种泳姿之一,一共五个约束)
A = [1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
% A = zeros(5,20);
% for i = 1:5
% A(i, (4*i-3): 4*i) = 1;
% end
b = [1;1;1;1;1];
% 线性等式约束的系数矩阵和常数项向量 (每种泳姿有且仅有一人参加,一共四个约束)
Aeq = [1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0;
0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0;
0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0;
0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1];
% Aeq = [eye(4),eye(4),eye(4),eye(4),eye(4)]; % 或者写成 repmat(eye(4),1,5)
beq = [1;1;1;1];
lb = zeros(20,1); % 约束变量的范围下限
ub = ones(20,1); % 约束变量的范围上限
%最后调用intlinprog()函数
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
% reshape(x,4,5)'
% 0 0 0 1 甲自由泳
% 1 0 0 0 乙蝶泳
% 0 1 0 0 丙仰泳
% 0 0 1 0 丁蛙泳
% 0 0 0 0 戊不参加
非线性规划:
非线性规划(Nonlinear Programming, NLP)是一种数学规划方法,用于解决目标函数或约束条件具有非线性项的优化问题。与线性规划不同,非线性规划包含了更为复杂的数学模型和求解过程。
一般形式的非线性规划可以表示为:
最小化(或最大化)目标函数:
[ f(x) ]
在给定约束条件下,求解决策变量 ( x ) 的最优解。
约束条件包括等式约束和不等式约束,可以表示为:
等式约束:
[ g_i(x) = 0, \quad i = 1, 2, \ldots, m ]
不等式约束:
[ h_j(x) \leq 0, \quad j = 1, 2, \ldots, n ]
其中, ( gi(x) ) 和 ( hj(x) ) 是函数,与决策变量 ( x ) 相关。
非线性规划的求解相对于线性规划更为困难,因为非线性函数引入了非凸性、多个局部最优解等问题。求解非线性规划通常需要使用迭代和数值优化方法,以逐步逼近全局最优解或局部最优解。
常见的非线性规划求解方法包括:
1.牛顿法(Newton’s Method):基于二阶导数信息进行迭代,可快速逼近局部最优解,但对初始点的选取敏感。
2.拟牛顿法(Quasi-Newton Methods):通过逐步逼近黑塞矩阵(Hessian Matrix),避免了计算二阶导数,常用的拟牛顿法包括DFP、BFGS等。
3.共轭梯度法(Conjugate Gradient Method):针对特定类型的二次优化问题,具有收敛速度快的特点。
4.遗传算法(Genetic Algorithms):基于生物进化的思想,通过模拟遗传、交叉和变异等操作,搜索最优解的全局性质。
5.粒子群优化(Particle Swarm Optimization):模拟鸟群或鱼群的行为,通过粒子的移动和信息共享来寻找最优解。
非线性规划在实际问题中广泛使用,包括经济学、工程设计、数据拟合、机器学习等领域。通过合适的数值优化算法和合理的问题建模,可以求解非线性规划问题并得到最优解。

Matlab求解:

列题:
参考代码:
主函数:
%% 非线性规划的函数
% [x,fval] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)
% x0表示给定的初始值(用行向量或者列向量表示),必须得写
% A b表示线性不等式约束
% Aeq beq 表示线性等式约束
% lb ub 表示上下界约束
% @fun表示目标函数
% @nonlfun表示非线性约束的函数
% option 表示求解非线性规划使用的方法
clear;clc
format long g %可以将Matlab的计算结果显示为一般的长数字格式(默认会保留四位小数,或使用科学计数法)
%% 例题1的求解
% max f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2
% s.t. -(x1-1)^2 +x2 >= 0 ; 2x1-3x2+6 >= 0
x0 = [0 0]; %任意给定一个初始值
A = [-2 3]; b = 6;
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1) % 注意 fun1.m文件和nonlfun1.m文件都必须在当前文件夹目录下
fval = -fval
% 一个值得讨论的地方,能不能把线性不等式约束Ax <= b也写到nonlfun1函数中?
% 先把nonlfun1中的c改为下面这样:
% c = [(x(1)-1)^2-x(2);
% -2*x(1)+3*x(2)-6];
% [x,fval] = fmincon(@fun1,x0,[],[],[],[],[],[],@nonlfun1)
% 结果也是可以计算出来的,但并不推荐这样做~
%% 使用其他算法对例题1求解
% edit fmincon % 查看fmincon的“源代码”
% Matlab2017a默认使用的算法是'interior-point' 内点法
% 使用interior point算法 (内点法)
option = optimoptions('fmincon','Algorithm','interior-point')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval
% 使用SQP算法 (序列二次规划法)
option = optimoptions('fmincon','Algorithm','sqp')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval %得到-4.358,远远大于内点法得到的-1,猜想是初始值的影响
% 改变初始值试试
x0 = [1 1]; %任意给定一个初始值
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option) % 最小值为-1,和内点法相同(这说明内点法的适应性要好)
fval = -fval
% 使用active set算法 (有效集法)
option = optimoptions('fmincon','Algorithm','active-set')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval
% 使用trust region reflective (信赖域反射算法)
option = optimoptions('fmincon','Algorithm','trust-region-reflective')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval
% this algorithm does not solve problems with the constraints you have specified.
% 这说明这个算法不适用我们这个约束条件,所以以后遇到了不能求解的情况,记得更换其他算法试试!!!
%% 选取初始值得到的结果可能会不满足限定条件,出现了一个Bug 因此选择的初始值很重要
x0 = [40.8, 10.8];
option = optimoptions('fmincon','Algorithm','interior-point')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval
% https://cn.mathworks.com/help/optim/ug/fmincon.html
%% 生成不同的随机初始值来优化代码,有一定几率会触发上面那个Bug,因此不推荐
n = 10; % 重复n次
Fval = +inf; X = [0,0]; %初始化最优的结果
A = [-2 3]; b = 6;
for i = 1:n
x0 = [rand()*10 , rand()*10]; %用随机数生成一个初始值(随机数的范围自己根据题目条件设置)
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option); % 注意 fun1.m文件和nonlfun1.m文件都必须在当前文件夹目录下
if fval < Fval % 如果找到了更小的值,那么就代替最优的结果
Fval = fval;
X = x;
end
end
Fval = -Fval
X
%% 使用蒙特卡罗的方法来找初始值(推荐)
clc,clear;
n=10000000; %生成的随机数组数
x1=unifrnd(-100,100,n,1); % 生成在[-100,100]之间均匀分布的随机数组成的n行1列的向量构成x1
x2=unifrnd(-100,100,n,1); % 生成在[-100,100]之间均匀分布的随机数组成的n行1列的向量构成x2
fmin=+inf; % 初始化函数f的最小值为正无穷(后续只要找到一个比它小的我们就对其更新)
for i=1:n
x = [x1(i), x2(i)]; %构造x向量, 这里千万别写成了:x =[x1, x2]
if ((x(1)-1)^2-x(2)<=0) & (-2*x(1)+3*x(2)-6 <= 0) % 判断是否满足条件
result = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ; % 如果满足条件就计算函数值
if result < fmin % 如果这个函数值小于我们之前计算出来的最小值
fmin = result; % 那么就更新这个函数值为新的最小值
x0 = x; % 并且将此时的x1 x2更新为初始值
end
end
end
disp('蒙特卡罗选取的初始值为:'); disp(x0)
A = [-2 3]; b = 6;
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1)
fval = -fval
%% 例题二的求解
x0 = [1 1 1]; %任意给定一个初始值
lb = [0 0 0]; % 决策变量的下界
[x,fval] = fmincon(@fun2,x0,[],[],[],[],lb,[],@nonlfun2) % 注意 fun2.m文件和nonfun2.m文件都必须在当前文件夹目录下
% x =
% 0.552167405729277 1.20325915507969 0.947824046150443
% fval =
% 10.6510918606939
%% 使用蒙特卡罗的方法来找初始值(推荐)
clc,clear;
n=1000000; %生成的随机数组数
x1= unifrnd(0,2,n,1); % 生成在[0,2]之间均匀分布的随机数组成的n行1列的向量构成x1
x2 = sqrt(2-x1); % 根据非线性等式约束用x1计算出x2
x3 = sqrt((3-x2)/2); % 根据非线性等式约束用x2计算出x3
fmin=+inf; % 初始化函数f的最小值为正无穷(后续只要找到一个比它小的我们就对其更新)
for i=1:n
x = [x1(i), x2(i), x3(i)]; %构造x向量, 这里千万别写成了:x =[x1, x2, x3]
if (-x(1)^2+x(2)-x(3)^2<=0) & (x(1)+x(2)^2+x(3)^2-20<=0) % 判断是否满足条件
result =sum(x.*x) + 8 ; % 如果满足条件就计算函数值
if result < fmin % 如果这个函数值小于我们之前计算出来的最小值
fmin = result; % 那么就更新这个函数值为新的最小值
x0 = x; % 并且将此时的x1 x2 x3更新为初始值
end
end
end
disp('蒙特卡罗选取的初始值为:'); disp(x0)
lb = [0 0 0]; % 决策变量的下界
[x,fval] = fmincon(@fun2,x0,[],[],[],[],lb,[],@nonlfun2) % 注意 fun2.m文件和nonfun2.m文件都必须在当前文件夹目录下
%% 例题三的求解(蒙特卡罗模拟那一讲的例题)
clear;clc
% 蒙特卡罗模拟得到的最大值为3445.6014
% 最大值处x1 x2 x3的取值为:
% 22.5823101903968 12.5823101903968 12.1265223966757
A = [1 -2 -2; 1 2 2]; b = [0 72];
x0 = [ 22.58 12.58 12.13];
Aeq = [1 -1 0]; beq = 10;
lb = [-inf 10 -inf]; ub = [inf 20 inf];
[x,fval] = fmincon(@fun3,x0,A,b,Aeq,beq,lb,ub,[]) % 注意没有非线性约束,所以这里可以用[]替代,或者干脆不写
fval = -fvalfun1-3:
function f = fun1(x)
% 注意:这里的f实际上就是目标函数,函数的返回值也是f
% 输入值x实际上就是决策变量,由x1和x2组成的向量
% fun1是函数名称,到时候会被fmincon函数调用, 可以任意取名
% 保存的m文件和函数名称得一致,也要为fun1.m
% max f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2
f = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ;
end
function f = fun2(x)
% f = x(1)^2+x(2)^2 +x(3)^2+8 ;
f = sum(x.*x) + 8; % 可别忘了x实际上是一个向量,我们可以使用矩阵的运算符号对其计算
end
function f = fun3(x)
f = -prod(x); % 可别忘了x实际上是一个向量(prod表示连乘符号,用法和sum类似)
end
nonlfun1-2:
function [c,ceq] = nonlfun1(x)
% 注意:这里的c实际上就是非线性不等式约束,ceq实际上就是非线性等式约束
% 输入值x实际上就是决策变量,由x1和x2组成的一个向量
% 返回值有两个,一个是非线性不等式约束c,一个是非线性等式约束ceq
% nonlfun1是函数名称,到时候会被fmincon函数调用, 可以任意取名,但不能和目标函数fun1重名
% 保存的m文件和函数名称得一致,也要为nonlfun1.m
% -(x1-1)^2 +x2 >= 0
c = [(x(1)-1)^2-x(2)]; % 千万別写成了: (x1-1)^2 -x2
ceq = []; % 不存在非线性等式约束,所以用[]表示
end
function [c,ceq] = nonlfun2(x)
% 非线性不等式约束
c = [-x(1)^2+x(2)-x(3)^2; % 一定要注意写法的规范,再次强调这里的x是一个向量!不能把x(1)写成x1
x(1)+x(2)^2+x(3)^2-20];
% 非线性等式约束
ceq = [-x(1)-x(2)^2+2;
x(2)+2*x(3)^2-3];
end
最大最小化模型:
在最不利的条件下求最有利的模型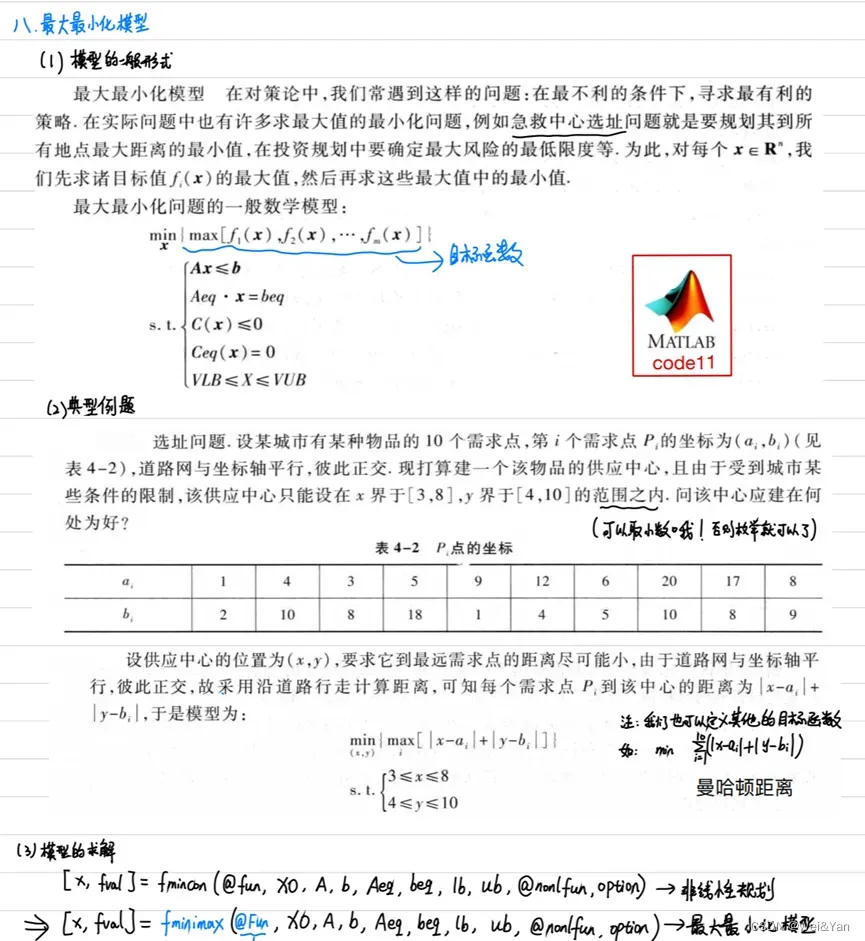

参考代码:
%% 最大最小化模型 : min{max[f1,f2,···,fm]}
x0 = [6, 6]; % 给定初始值
lb = [3, 4]; % 决策变量的下界
ub = [8, 10]; % 决策变量的上界
[x,feval] = fminimax(@Fun,x0,[],[],[],[],lb,ub)
max(feval)
% x =
% 8.0000 8.5000
% feval =
% 13.5000 5.5000 5.5000 12.5000 8.5000 8.5000 5.5000 13.5000 9.5000 0.5000
% 结论:
% 在坐标为(8,8.5)处建立供应中心可以使该点到各需求点的最大距离最小,最小的最大距离为13.5单位。
fun:
%两种求曼哈顿距离方法:
function f = Fun(x)
a=[1 4 3 5 9 12 6 20 17 8];
b=[2 10 8 18 1 4 5 10 8 9];
% 函数向量
f=zeros(10,1);
for i = 1:10
f(i) = abs(x(1)-a(i))+abs(x(2)-b(i));
end
% f(1) = abs(x(1)-a(1))+abs(x(2)-b(1));
% f(2) = abs(x(1)-a(2))+abs(x(2)-b(2));
% f(3) = abs(x(1)-a(3))+abs(x(2)-b(3));
% f(4) = abs(x(1)-a(4))+abs(x(2)-b(4));
% f(5) = abs(x(1)-a(5))+abs(x(2)-b(5));
% f(6) = abs(x(1)-a(6))+abs(x(2)-b(6));
% f(7) = abs(x(1)-a(7))+abs(x(2)-b(7));
% f(8) = abs(x(1)-a(8))+abs(x(2)-b(8));
% f(9) = abs(x(1)-a(9))+abs(x(2)-b(9));
% f(10) = abs(x(1)-a(10))+abs(x(2)-b(10));
end
多目标规划:

参考代码:
%% 多目标规划问题
w1 = 0.4; w2 = 0.6; % 两个目标函数的权重 x1 = 5 x2 = 2
w1 = 0.5; w2 = 0.5; % 两个目标函数的权重 x1 = 5 x2 = 2
w1 = 0.3; w2 = 0.7; % 两个目标函数的权重 x1 = 1 x2 = 6
c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3]; % 线性规划目标函数的系数
A = [-1 -1]; b = -7; % 不等式约束
lb = [0 0]'; ub = [5 6]'; % 上下界
[x,fval] = linprog(c,A,b,[],[],lb,ub)
f1 = 2*x(1)+5*x(2)
f2 = 0.4*x(1) + 0.3*x(2)
%% 敏感性分析
clear;clc
W1 = 0.1:0.001:0.5; W2 = 1- W1;
n =length(W1);
F1 = zeros(n,1); F2 = zeros(n,1); X1 = zeros(n,1); X2 = zeros(n,1); FVAL = zeros(n,1);
A = [-1 -1]; b = -7; % 不等式约束
lb = [0 0]; ub = [5 6]; % 上下界
for i = 1:n
w1 = W1(i); w2 = W2(i);
c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3]; % 线性规划目标函数的系数
[x,fval] = linprog(c,A,b,[],[],lb,ub);
F1(i) = 2*x(1)+5*x(2);
F2(i) = 0.4*x(1) + 0.3*x(2);
X1(i) = x(1);
X2(i) = x(2);
FVAL(i) = fval;
end
% 「Matlab」“LaTex字符汇总”讲解:https://blog.csdn.net/Robot_Starscream/article/details/89386748
% 在图上可以加上数据游标,按住Alt加鼠标左键可以设置多个数据游标出来。
figure(1)
plot(W1,F1,W1,F2)
xlabel('f_{1}的权重')
ylabel('f_{1}和f_{2}的取值')
legend('f_{1}','f_{2}')
figure(2)
plot(W1,X1,W1,X2)
xlabel('f_{1}的权重')
ylabel('x_{1}和x_{2}的取值')
legend('x_{1}','x_{2}')
figure(3)
plot(W1,FVAL) % 看起来是两个直线组合起来的下半部分
xlabel('f_{1}的权重')
ylabel('综合指标的值')
版权声明:本文为博主作者:Cocobol0原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/weixin_73612682/article/details/132356318
