相机标定
相机在计算机视觉方面的一些应用一般需要相机标定。我们总是听到标定这个词,那么具体标定的是什么呢?相机的拍摄是一个三维到二维(透视投影)的过程,这个过程可以用数学模型去表述,标定便是计算这个数学模型中的参数,我们最终希望通过这些参数能够从二维的图像去还原三维的世界。
拍照过程简化(针孔相机模型)
拍照是一个三维世界降维到二维的不可逆的操作,可以说相机拍摄是一个 的变换。
相机标定的目的就是找到一个合适的数学模型,近似表示这个三维到二维的过程,并且求其逆过程。
实际的镜头模组都是非常复杂的,我们可以找一个与这个镜头具有相同的物像共轭关系的凸透镜来等效这个镜头,我们把这个凸透镜称作等效透镜。为了分析的方便,我们用一个等效透镜在数学上替代一整个镜头模组。
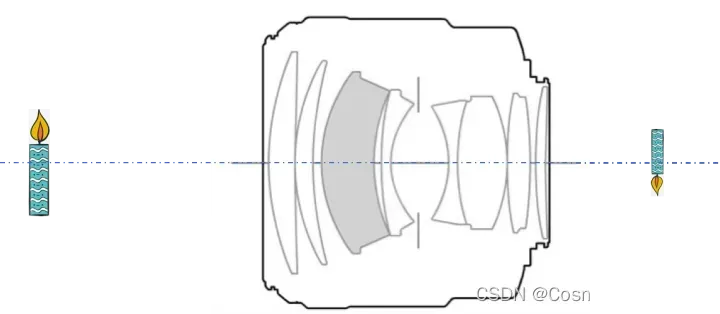 |  |
|---|---|
| Canon EF 85mm/F1.2L II USM 镜头模组 | 等效透镜 |
简化后的针孔相机模型中的 f 为焦距,但是这个焦距不是等效透镜的焦距,而是指图像传感器到等效透镜光心 O 的距离。
针孔相机模型大大简化了相机模型的数学复杂度,但是也有一些代价。针孔相机模型没有考虑相差(镜头畸变),没有考虑景深(因为针孔成像没有焦距的概念,认为物总是能够清晰成像)。
我们以小米 12S Ultra 的主摄为例,Sony IMX989 就是该款主摄的 CMOS 图像传感器。即便手机中的相机模组体积很紧凑,其中也是有多片镜头的,右下图是主摄的镜头组拆解,左图说的 23mm 等效焦距就是指跟这一堆镜片等效的等效镜片到 CMOS 的距离。像素尺寸指的是一个 CMOS 像素的边长,一个(正方形)像素尺寸约为 1.6μm。四合一像素尺寸是四个像素合成一个像素,所以边长 3.2μm。
相机内参
相机拍摄过程中的四个坐标系
下图表示了摄影的过程,其实计算机视觉可以说是摄影或计算机图形学(Computer Graphics)的逆过程,想着如何利用已经降维成2D的信息去还原3D世界中的信息。
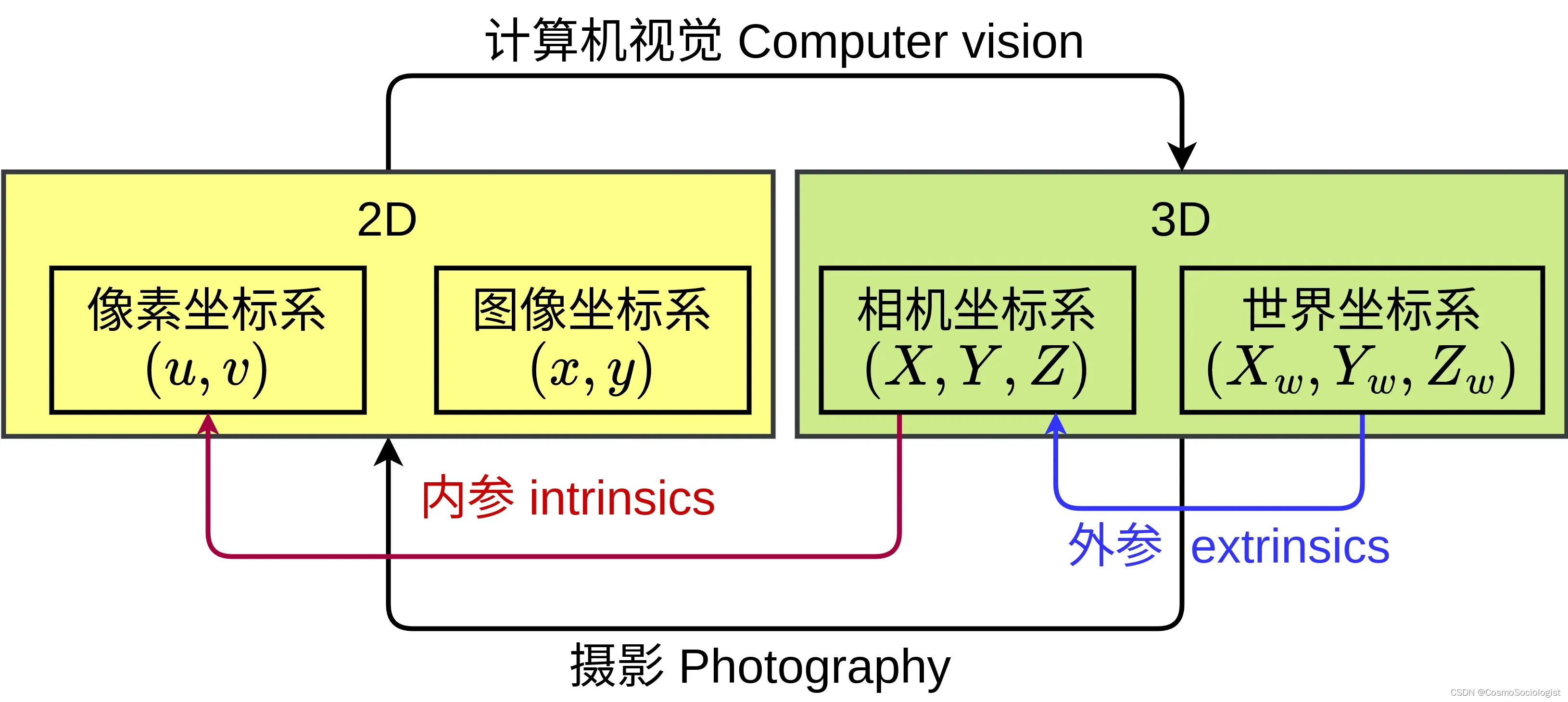
这里使用四个坐标系来描述拍摄过程:像素坐标系、图像坐标系、相机坐标系、世界坐标系。
像素坐标系:图片是由像素组成的,每个像素可以用一个有序二元组(u,v)来表示,这个坐标系就叫做像素坐标系。像素坐标系是一个二维坐标系,标识了在每个像素在图像传感器中的位置,每次增量是 1 个像素。
图像坐标系:像素坐标系中的标号为(u,v),其中 u 轴对应实际物理尺寸 dx,v 轴对应实际物理尺寸 dy,图像坐标系是一个对应真实世界的尺寸二维坐标系,可以记为 。图像坐标系也标记的是像素在图像传感器中的位置,不过增量是每个像素的实际物理尺寸,比如上面提到的 IMX989 的每个像素尺寸 1.6μm,对应这里的dx和dy。
相机坐标系:以相机光心为原点呈现的世界三维坐标系 ,坐标系原点是相机等效镜头的光心。
世界坐标系:真实的世界三维坐标系 ,坐标系原点一般是外界的某一点。比如在机器人应用中经常是以机器人的基座为世界坐标系原点。
| 像素坐标系 | 图像坐标系 | 相机坐标系 | 世界坐标系 |
|---|---|---|---|
| 2D 坐标系,位于 CMOS | 3D 坐标系 | ||
| 整数序号,标识像素位置, 原点位于 CMOS 左上角 | 对应真实世界物理尺寸, 标识像素在 CMOS 上的平面位置, 原点为相机光轴与 CMOS 的交点。 | 原点为相机光心 | 世界坐标系原点 |
相机拍照的过程可以分为以下几步:
- 将世界坐标转换为相机坐标,存在刚体变换。其实对应的就是相机外参。
- 相机坐标变为图像坐标,这是一个 3D->2D 的透视投影过程。
- 图像坐标变为像素坐标,对图像坐标系进行离散化。
相机内参
相机内参便是求第二步和第三步中的参数。
为了描述的方便,我们可以将针孔相机模型翻转过来,如下图所示,因为主要用到三角关系,所以翻转前后在数学描述上是等价的。
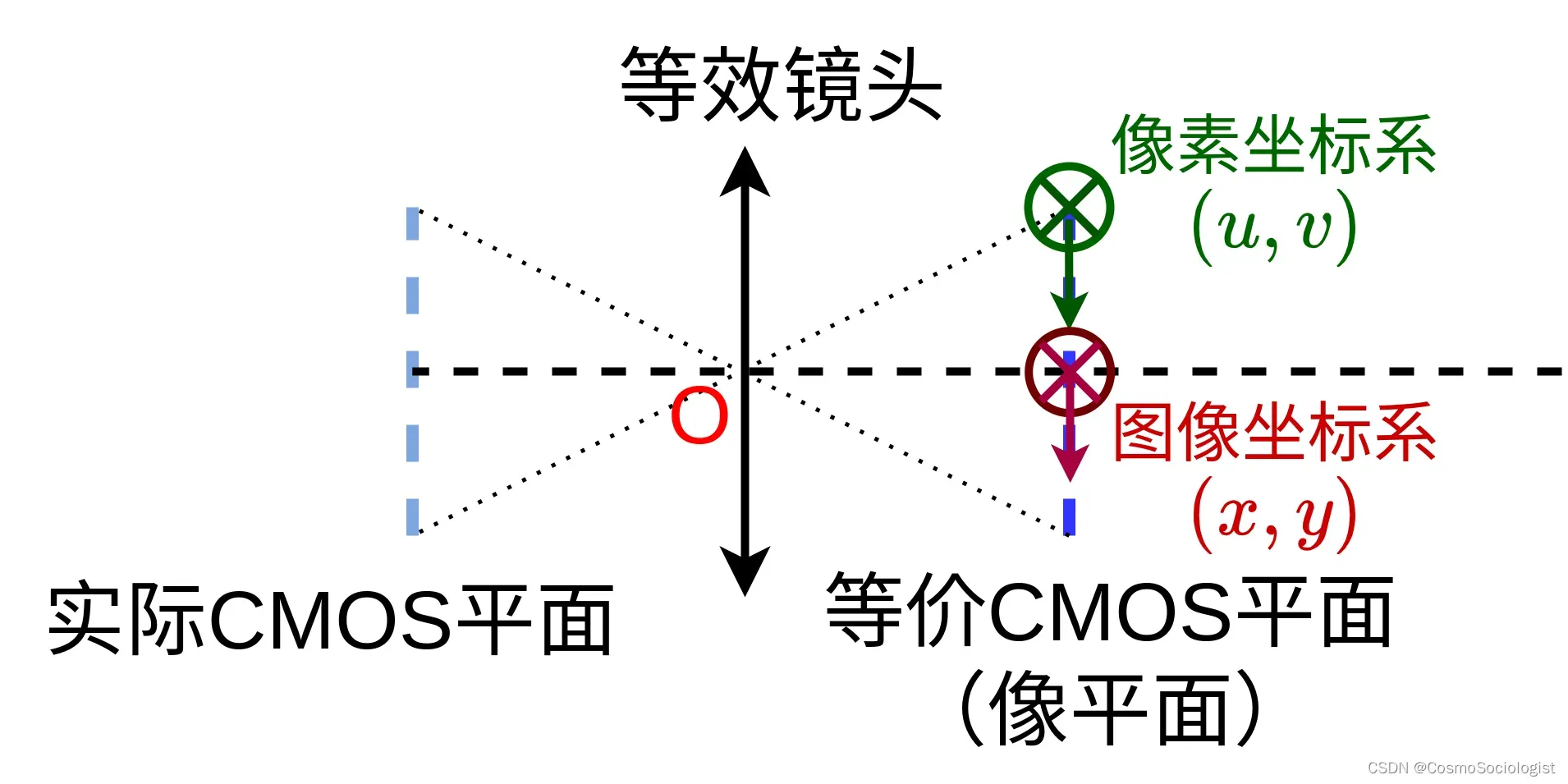
在相机坐标系中,像平面(图像传感器所在平面)为 (焦距,mm)。空间中一点 P 在相机坐标系下为
,该点在像平面上的投影为点
,在图像坐标系下为
,在像素坐标系中的坐标为
。
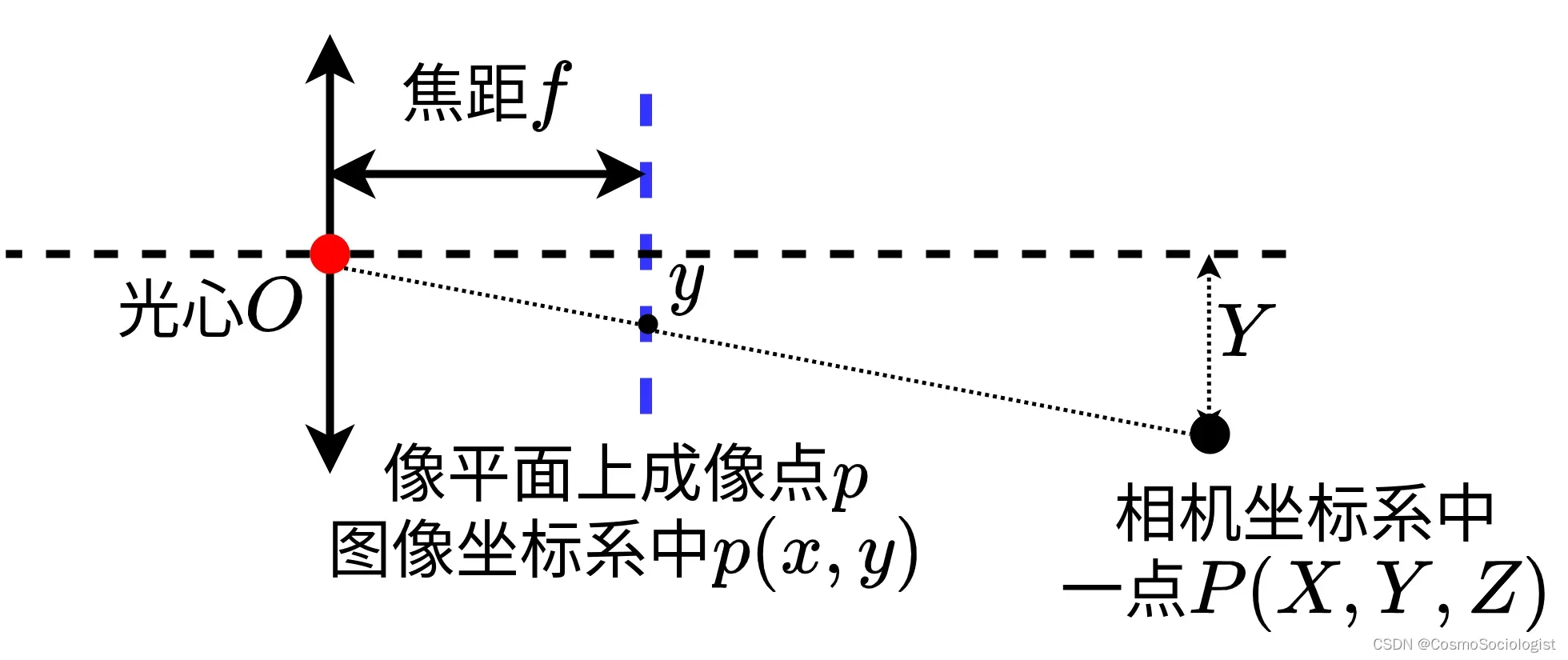
根据三角形相似原理,通过右图可得图像坐标系和相机坐标系比例关系
相机坐标系(3D) -> 图像坐标系(2D):于是我们 得到了 相机坐标系中一3D点 在图像坐标系中的对应平面位置
像素坐标系的原点位于图像传感器的左上角,记光心到 CMOS 零点的偏移为 ,也就是相机光心在像素坐标系中的坐标为
。记每个像素在水平和竖直方向上的尺寸为
(mm/pixel),由于像素不一定是正方形的,所以这里长宽分别表示,这个就对应上面说的CMOS像素尺寸1.6μm。
图像坐标系(连续2D) -> 像素坐标系(离散2D):则图像坐标系中一点 到像素坐标系中像素标号
的关系可以表示为
令 ,则上面两式可以写成
其中 (pixel)为像素焦距,即单位长度的像素个数,单位为像素。
上式写成矩阵形式为
上面的矩阵可以写成 ,中间的矩阵便是内参(intrinsics)矩阵,其中的四个参数便是要标定的内参。这个矩阵描述了相机坐标系到像素坐标系的变换关系。
有了相机内参我们便可以知道像素点对应的归一化平面(距光心距离为1的平面)的 x y 坐标,注意不是真实的XY坐标,因为空间点的深度值在透视投影过程中丢失了。
畸变
畸变(distortion)是对直线投影(rectilinear projection)的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。畸变简单来说就是一条直线投影到图片上不能保持为一条直线了,这是一种光学畸变(optical aberration),可能是摄像机镜头的原因。
畸变模型:桶形畸变和枕形畸变。
相机中透镜的加入会对光线传播产生影响。透镜自身形状会影响光线传播,这种畸变(distortion,或失真)称为径向畸变;再者,相机组装过程中,镜片平面和 CMOS 不可能绝对平行,这种透镜平面和 CMOS 成像面不平行导致的畸变叫 切向畸变。
如果镜头没有畸变,那么点 P、光心 O、像点 p 应该是共线的。
径向畸变可以理解为像点沿距光心的长度方向发生了变化,切向畸变可以理解为像点沿切向(长度正交方向)发生了变化。一般使用多项式描述这些畸变, 来描述畸变后的像点位置
径向畸变
切向畸变
像平面(图像坐标系)上畸变后的像点坐标为
得到 5 个畸变参数 后便可以对畸变进行建模。实际使用中也可以使用更简单的模型,比如径向畸变只使用二阶(只用
)多项式描述。
外参
内参是确定像素坐标系到图像坐标系的四个参数
世界坐标系到相机坐标系的变换矩阵 称为外参。
比如和机器人相关的应用中,一般外参是描述相机坐标系和机器人基坐标系之间的刚体变换。
如果有标定板的话,标定板的尺寸都是已知的。
参考
Computer Vision: A Modern Approach
文章出处登录后可见!


