目录

• savgol_filter简介
• savgol_filter原理
• 参数window_length对平滑的效果
• 参数polyorder的平滑效果

savgol_filter简介

Savitzky-Golay滤波器最初由Savitzky和Golay于1964年提出，是光谱预处理中常用滤波方法，它的核心思想是对一定长度窗口内的数据点进行k阶多项式拟合，从而得到拟合后的结果。对它进行离散化处理后后，Ｓ-Ｇ 滤波其实是一种移动窗口的加权平均算法，但是其加权系数不是简单的常数窗口，而是通过在滑动窗口内对给定高阶多项式的最小二乘拟合得出。这种滤波器最大的特点在于在滤除噪声的同时可以确保信号的形状、宽度不变。

它对信号的操作是在时域内对window_length内的数据进行多项式拟合。而从频域上看，这种拟合实际就是通过了低频数据，而滤掉了高频数据。

这种滤波其实是一种移动窗口的加权平均算法，但是其加权系数不是简单的常数窗口，而是通过在滑动窗口内对给定高阶多项式的最小二乘拟合得出。

总之，平滑滤波是光谱分析中常用的预处理方法之一。用Savitzky-Golay方法进行平滑滤波，可以提高光谱的平滑性，并降低噪音的干扰。S-G平滑滤波的效果，随着选取窗宽不同而不同，可以满足多种不同场合的需求。

savgol_filter原理

表达式为：
scipy.signal.savgol_filter(x, window_length, polyorder)

详细表达式和定义可以查看下面链接：
https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.savgol_filter.html

参数的含义：

1、x为要滤波的信号；

2、window_length即窗口长度；取值为奇数且不能超过len(x)。它越大，则平滑效果越明显；越小，则更贴近原始曲线。

3、polyorder为多项式拟合的阶数。它越小，则平滑效果越明显；越大，则更贴近原始曲线。

参数window_length对平滑的效果

import os
import matplotlib.pyplot as plt
import scipy.signal
import numpy as np

def main():
    # 项目目录
    dir = "D:\\a_user_file\\8_data"
    filename = '1.csv'
    path = os.path.join(dir, filename)
    with open(path, "r") as fname:
        data = fname.read()
        lines = data.split("\n")
        lines = lines[1:5000]
        raw_data = []
        for i in range(len(lines)):
            line_i = lines[i].split(",")
            raw_data.append(int(line_i[4]))
    #sig = denoise(raw_data)
    sig = raw_data
    tmp_smooth1 = scipy.signal.savgol_filter(sig, 21, 3)
    tmp_smooth2 = scipy.signal.savgol_filter(sig, 53, 3)
    plt.subplot(3,1,1)
    plt.plot(sig)
    # plt.semilogx(sig, label='mic')
    plt.subplot(3,1,2)
    plt.plot(tmp_smooth1 * 0.5, label='mic'  + '拟合曲线-21', color='red')
    plt.subplot(3,1,3)
    plt.plot(tmp_smooth2 * 0.5, label='mic'  + '拟合曲线-53', color='green')
    plt.show()

main()

结果显示为：

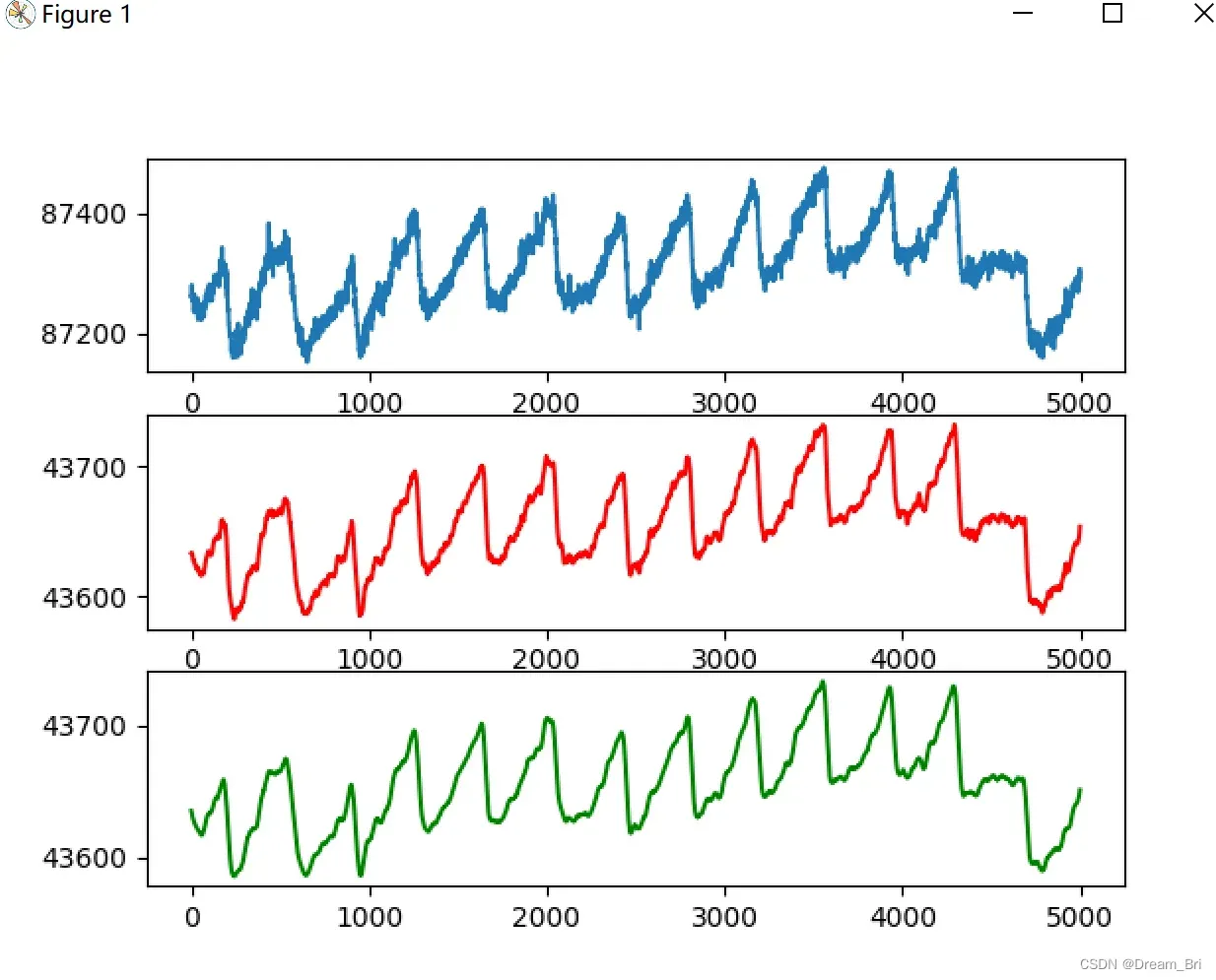
可以看到，window_length的值越小，曲线越贴近真实曲线；window_length值越大，平滑效果越厉害。

参数polyorder的平滑效果

代码如下：

import os
import matplotlib.pyplot as plt
import scipy.signal
import numpy as np

def main():
    # 项目目录
    dir = "D:\\a_user_file\\8_data"
    filename = '1.csv'
    path = os.path.join(dir, filename)
    with open(path, "r") as fname:
        data = fname.read()
        lines = data.split("\n")
        lines = lines[1:5000]
        raw_data = []
        for i in range(len(lines)):
            line_i = lines[i].split(",")
            raw_data.append(int(line_i[4]))
    #sig = denoise(raw_data)
    sig = raw_data
    tmp_smooth1 = scipy.signal.savgol_filter(sig, 53, 9)
    tmp_smooth2 = scipy.signal.savgol_filter(sig, 53, 3)
    plt.subplot(3,1,1)
    plt.plot(sig)
    # plt.semilogx(sig, label='mic')
    plt.subplot(3,1,2)
    plt.plot(tmp_smooth1 * 0.5, label='mic'  + '拟合曲线-21', color='red')
    plt.subplot(3,1,3)
    plt.plot(tmp_smooth2 * 0.5, label='mic'  + '拟合曲线-53', color='green')
    plt.show()

main()

显示的效果如下：

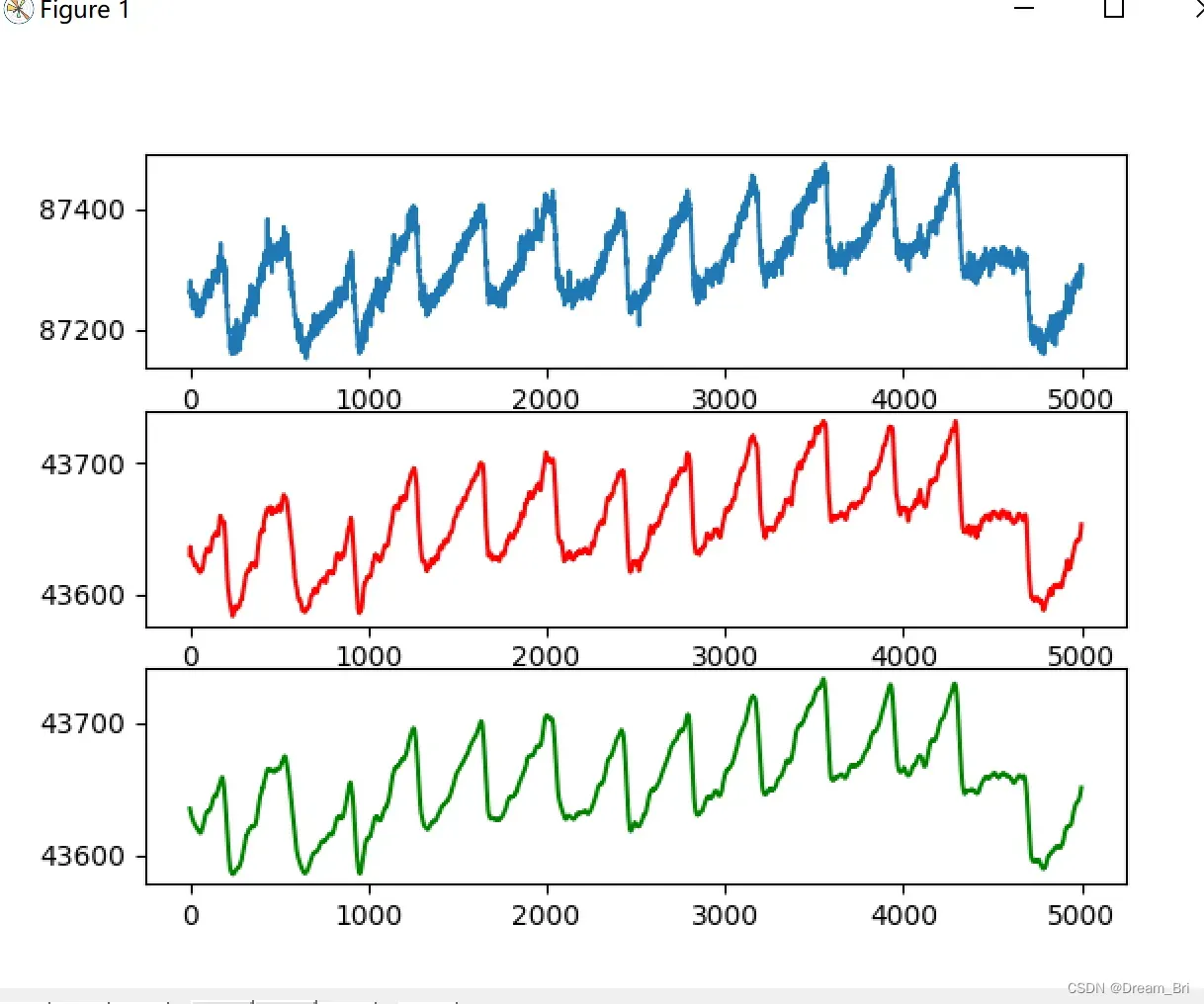
可以看出参数polyorder(多项式阶数)越大，曲线越贴近真实曲线；polyorder值越小，曲线平滑越厉害。

注：当polyorder值较大时，受窗口长度限制，拟合会出现问题，高频曲线会变成直线，

参考：
https://blog.csdn.net/sinat_21258931/article/details/79298478
https://blog.csdn.net/weixin_43821212/article/details/100016021
https://blog.csdn.net/kaever/article/details/105520941