先做一个声明：文章是由我的个人公众号中的推送直接复制粘贴而来，因此对智能优化算法感兴趣的朋友，可关注我的个人公众号：启发式算法讨论。我会不定期在公众号里分享不同的智能优化算法，经典的，或者是近几年提出的新型智能优化算法，并附MATLAB代码。

先放一个链接：

算法应用：基于DBO算法的工程优化设计(第1期)(含MATLAB代码)

这一期的推送是接之前的第1期。这些优化设计问题在一些外文或中文期刊上也被讨论和研究，实际上就是算法的进一步应用。所以大家在改进算法后，跑一跑测试集，验证算法性能，然后再应用到这些问题中。
 

这一期利用几种较新的智能优化算法去求解这些工程领域中的实际问题。选取了五种近几年的算法：蜣螂优化(DBO)、哈里斯鹰优化(HHO)、白鲸优化(BWO)、金豺优化(GJO)和蛇优化(SO)。不清楚这几种算法的，可以先看我往期的推送，了解它们的算法原理和计算流程。

2022年的DBO：蜣螂优化(DBO)算法(含MATLAB代码)

2019年的HHO：哈里斯鹰优化(HHO)算法(含MATLAB代码)

2022年的BWO：白鲸优化(BWO)算法(含MATLAB代码)

2022年的GJO：金豺优化(GJO)算法(含MATLAB代码)

2022年的SO：SO算法(含代码)

01
优化问题模型

工程领域有许多优化设计问题，接着上一期，今天介绍更复杂的6种：焊接梁设计、多盘离合器制动器设计问题、步进圆锥滑轮问题、减速机设计问题、行星轮系设计优化问题、机器人夹持器问题。这些优化设计都是在满足各种约束条件下，使得材料花销最少、或质量最小、或体积最小等。因此，它们的数学模型都是单目标或多目标的约束优化模型。今天介绍的6个问题和上期一样，都属于单目标约束优化。

1.1 焊接梁设计

如图1所示，焊接梁结构由梁a和连接到构件b的焊接组成，这个问题受到一些约束，包括:剪切应力(t)、梁内弯曲应力(O)、杆上屈曲载荷(Pe)和梁端挠度(8)。要解决这个问题，需要定位焊接梁设计的下列结构参数的可能组合:焊缝厚度(h)、夹紧棒材长度(I)、棒材高度(t)、棒材厚度(b)。这些参数用向量表示:x= [x1,x2,x3,x4]，其中x1,x2,x3,x4分别代表h, I, t, b。

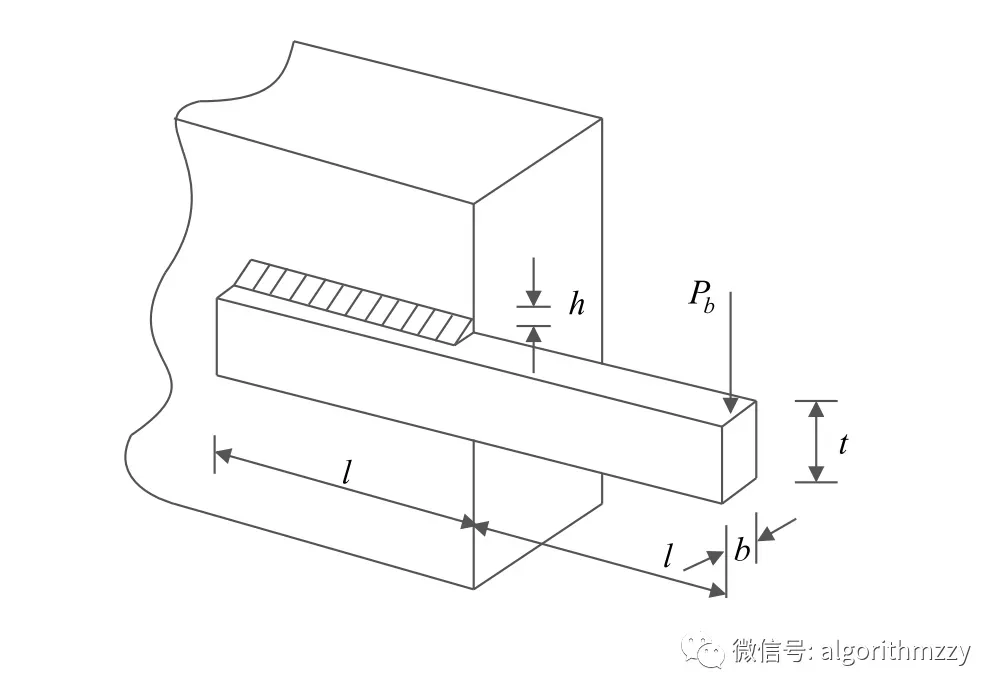
图1 焊接梁设计

该问题的主要目标是设计成本最小的焊接梁。该问题包含5个约束条件，采用4个变量对焊接梁进行求解。这个问题的数学描述可以定义如下：

1.2 多盘离合器制动器设计问题

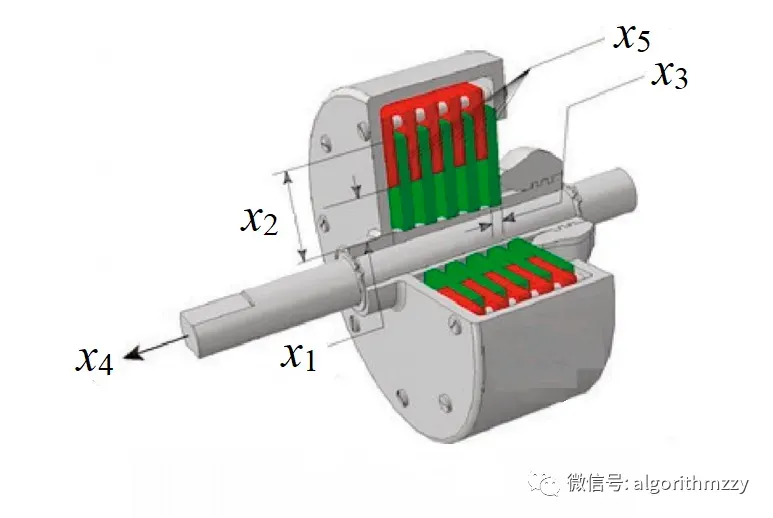
图2 多盘离合器制动器设计问题

该问题的主要目标是使多片离合器制动器的质量最小化。在该问题中，使用了5个整数决策变量，分别是内半径(ri)、外半径(ro)、圆盘厚度(t)、因子力(F)和若干摩擦面(Z)，该问题的结构参数如图2所示。这个问题包含9个非线性约束。这个问题的定义如下：

1.3 步进圆锥滑轮问题

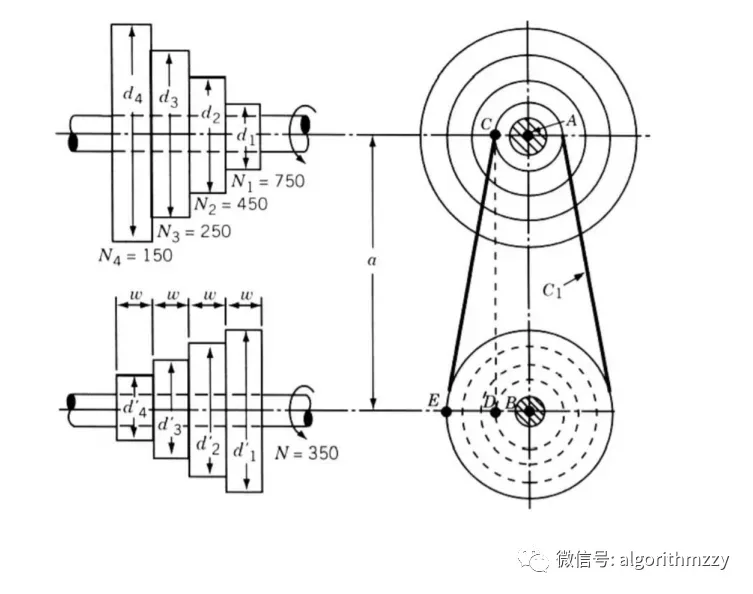
图3 步进圆锥滑轮问题

如图3所示，这个问题的主要目标是用5个变量使4个阶梯锥滑轮的重量最小化，其中4个变量是滑轮每一级的直径，最后一个变量是滑轮的宽度。该问题包含11个非线性约束，以确保发射功率必须在0.75 hp。这个问题的数学模型定义如下：

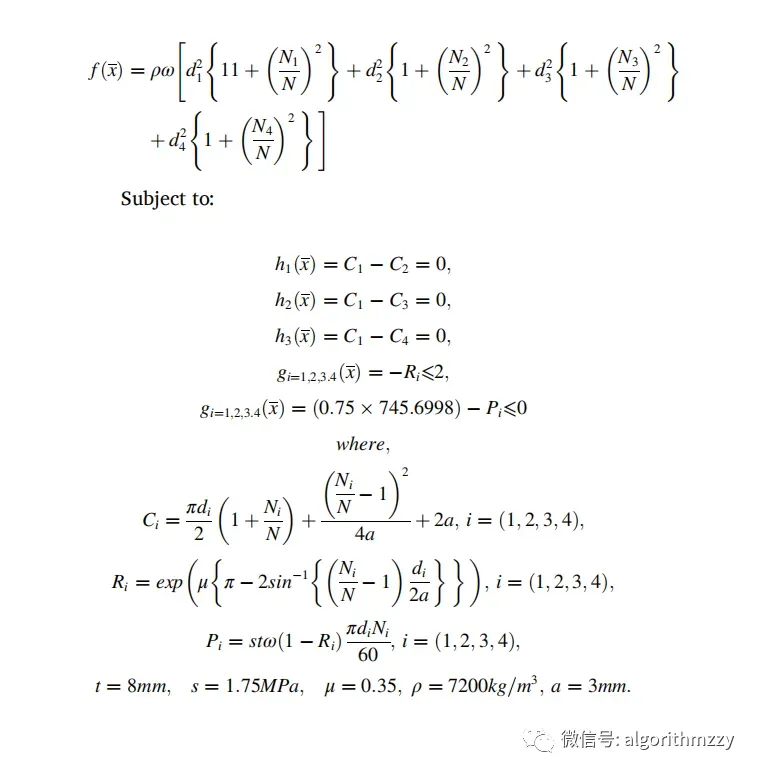
1.4 减速机设计问题

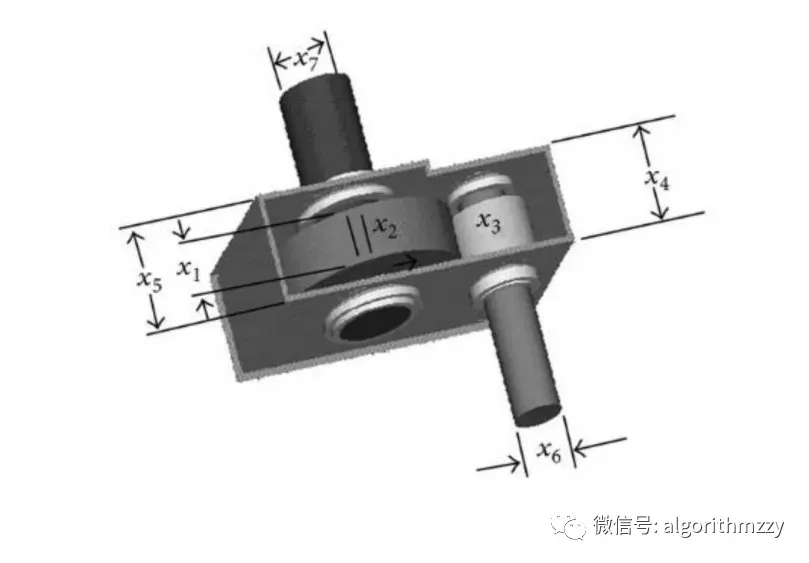
图4 减速机设计问题

减速器设计问题是一个工程设计问题。它有7个设计变量，如图4所示。本设计问题的主要目标是在满足以下约束条件的情况下使减速器的重量最小化：齿轮齿的弯曲应力、表面压力、轴的横向偏转、轴上的应力。有7个设计变量(z1-z7)，如面宽(b)，齿的模块(m)，齿轮齿数(p)，轴承之间的第一轴的长度(l1)，轴承之间的第二轴的长度(l2)，第一轴的直径(di)，第二轴的直径(d2)。该问题的数学公式描述如下：

1.5 行星轮系设计优化问题

这个问题的主要目标是使汽车齿轮传动比的最大误差最小化。为了使最大误差最小化，计算了自动行星传动系统的总齿数。该问题包含6个整数变量和11个不同几何约束和装配约束。这个问题可以定义如下：

1.6 机器人夹持器问题

在该问题中，将机器人夹持器产生的最小力与最大力之间的差作为目标函数。该问题包含与机器人相关的7个设计变量和6个非线性设计约束。数学上，这个问题的定义如下：

02
约束条件处理

约束处理方法主要分为3类：罚函数方法、可行规则方法和多目标方法。

因原理简单和易于实现，罚函数方法是目前应用广泛的约束处理方法之一。罚函数方法是在目标函数中加入一个惩罚函数将约束问题转换成一个无约束问题，该方法的难点在于罚函数的选择。常用的罚函数方法主要有3种：死罚函数方法、静态罚函数方法和自适应罚函数方法。

可行规则方法建立在可行解要优于不可行解的偏好基础上，3条比较规则为:可行解要优于不可行解;当两个都是可行解时，选择目标函数值小的解;当两个都是不可行解时，选择违反约束小的解。

近年来，多目标概念已经越来越多地用于进化计算中的约束处理问题，其思想是将约束转换成一个或多个目标。根据处理约束的不同原则，有两类多目标方法：一类是有两个目标的，如源目标函数和所有约束违反程函数；另一类是将每个约束看成一个目标。因此，对于有m个约束的约束问题来说，总共有m+1个目标函数。

惩罚函数是最流行的约束处理方法，因为它简单且易于实现。为了简单起见，这里使用文献[1]中的惩罚方法来处理这些工程优化设计问题的约束条件，这是一种常见的罚函数：

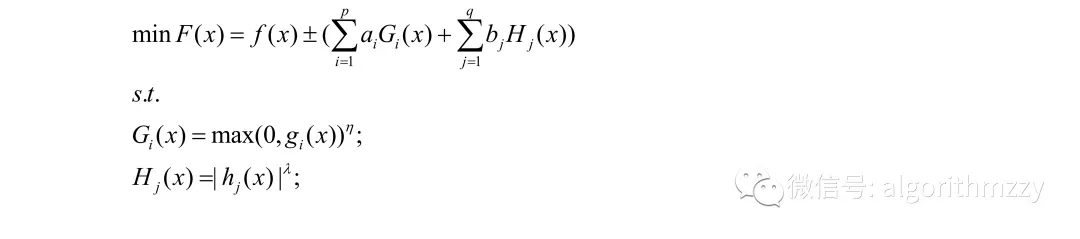
G𝑖(𝒙)是不等式约束，H𝑗(𝒙)是等式约束，𝑝是不等式约束的数量，𝑞是等式约束的数量，𝑎𝑖和𝑏𝑗是正的常数，𝜂和𝜆等于1或2。对于这种惩罚方法，当候选解违反任何约束时，目标函数值都会增加，将种群从不可行解推入可行域内。

这里是采用了文献[1]中一个比较经典的罚函数方法，旨在做简单的演示。实际上，大家也可以改用其他的罚函数方法，例如文献[2]中提出的Oracle罚函数方法，或者使用其他的约束处理技术。此外，利用智能优化算法求解约束优化问题时，除了算法上的改进外，也可以在约束条件的处理技术上做创新。比如文献[2]提出了一种改进的Oracle罚函数方法，并嵌入到差分进化(DE)算法中。文献[3]在算法和约束处理上都做了改进。

03
实验结果

将约束处理后的数学模型，利用上述的五种智能优化算法进行求解。为了对比性能，记录了它们在10次运行结果中的最差值(Worst)、中位数(Median)、最佳值(Best)、均值(Mean)和标准差(Std)。这里是为了方便只运行了10次，实际上，为了保持科学性，应该是至少要运行三五十次~

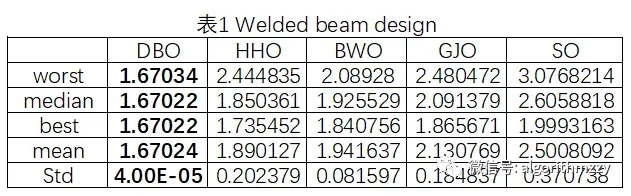
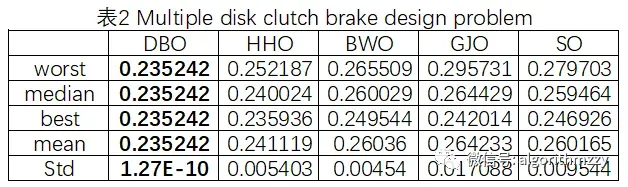
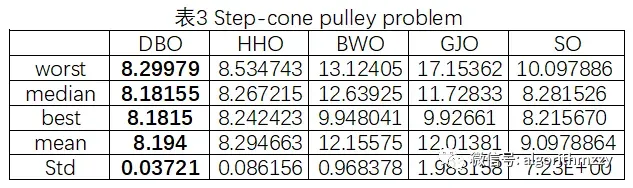
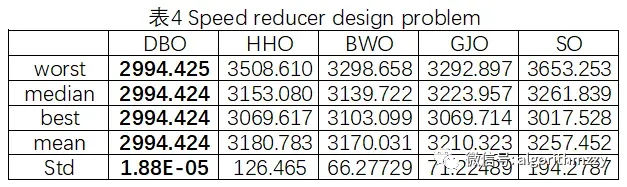
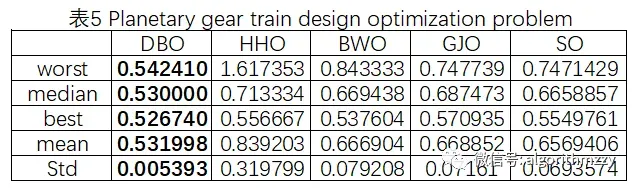
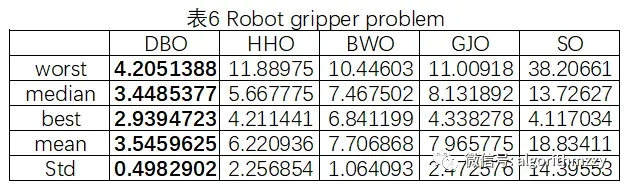
三种算法最大迭代次数为1000。取10次运行中相应指标结果进行展示。对比结果如表1~表6所示，其中，五种算法中的最优结果用粗体表示；收敛曲线如图5~图10所示。这里就不再进一步做分析和讨论了。

(下面需要注意的是，收敛曲线画的是均值收敛曲线。运行了10次，取每一代的平均值来画。也可以使用中位数。因为是随机算法，有可能你的算法就偶然一次收敛效果很优秀，然后你就用那一次来画，并放到论文里，并宣称很NB。这样不具科学性，应该多次运行，画均值收敛曲线~)

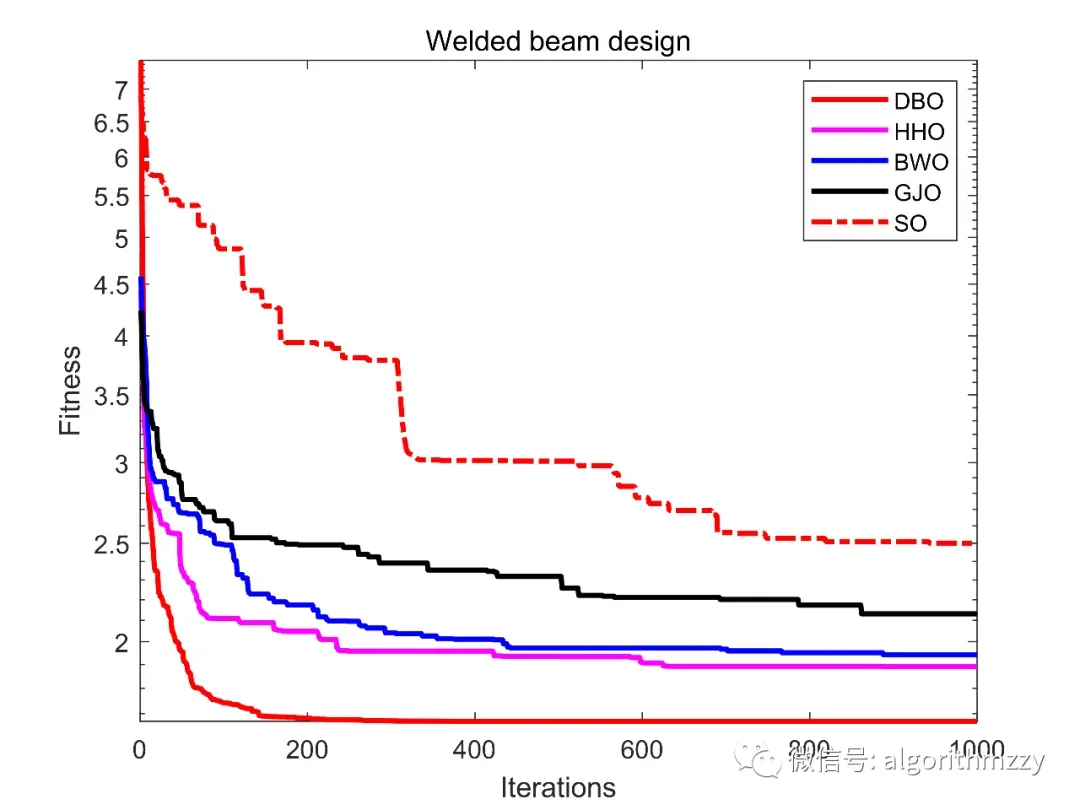
图5 Welded beam design

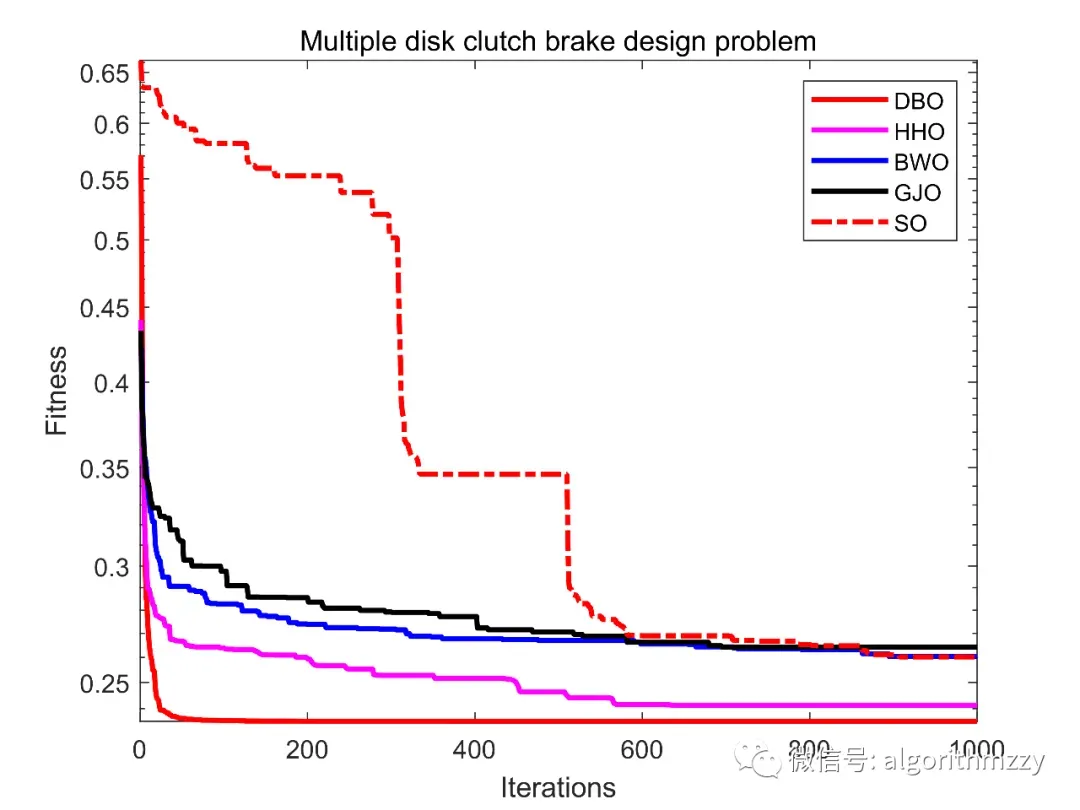
图6 Multiple disk clutch brake design problem

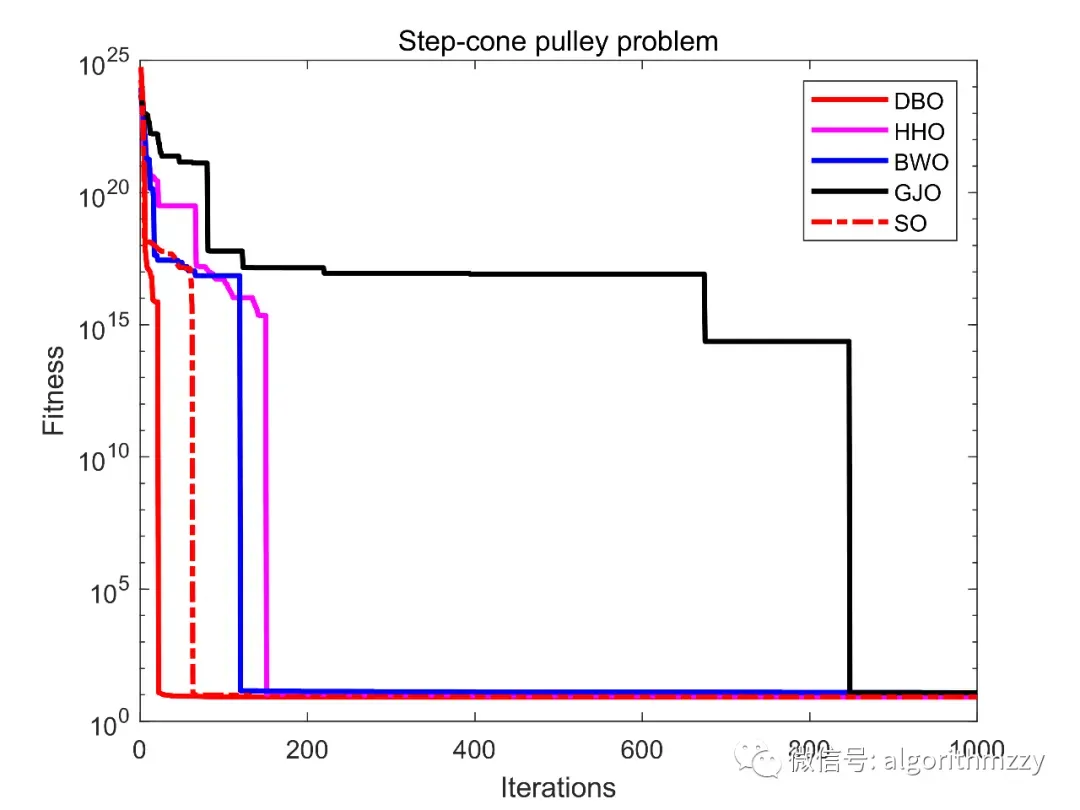
图7 Step-cone pulley problem

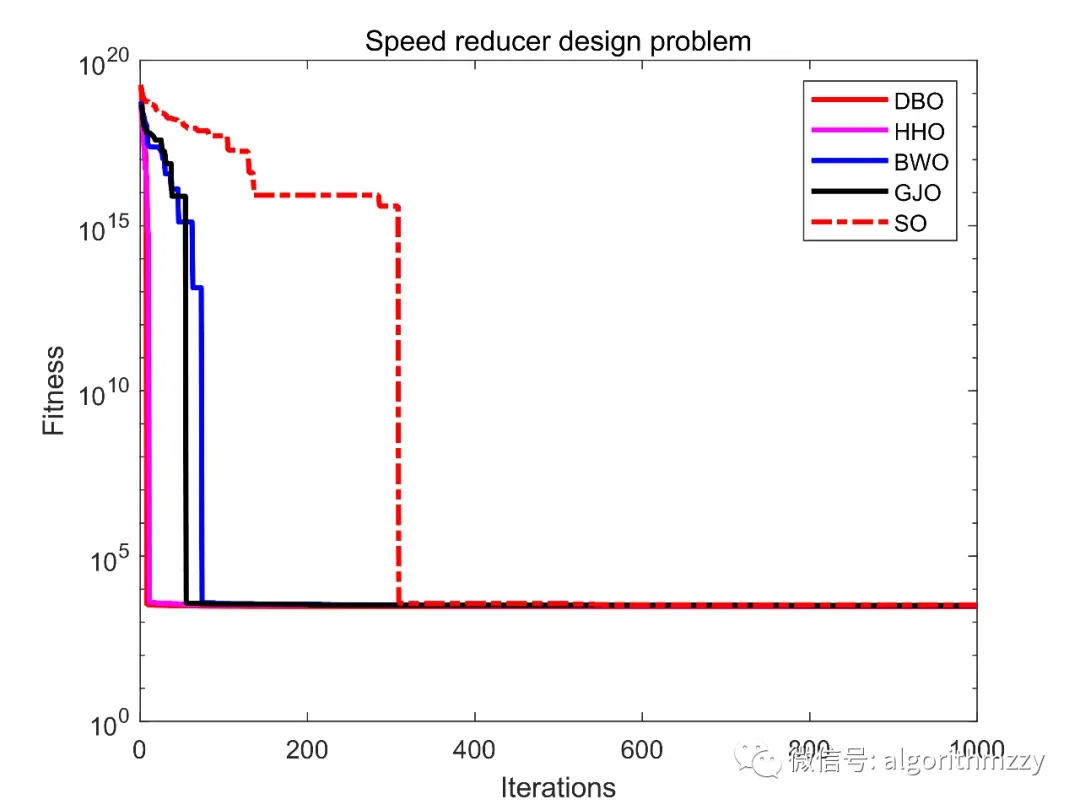
图8 Speed reducer design problem

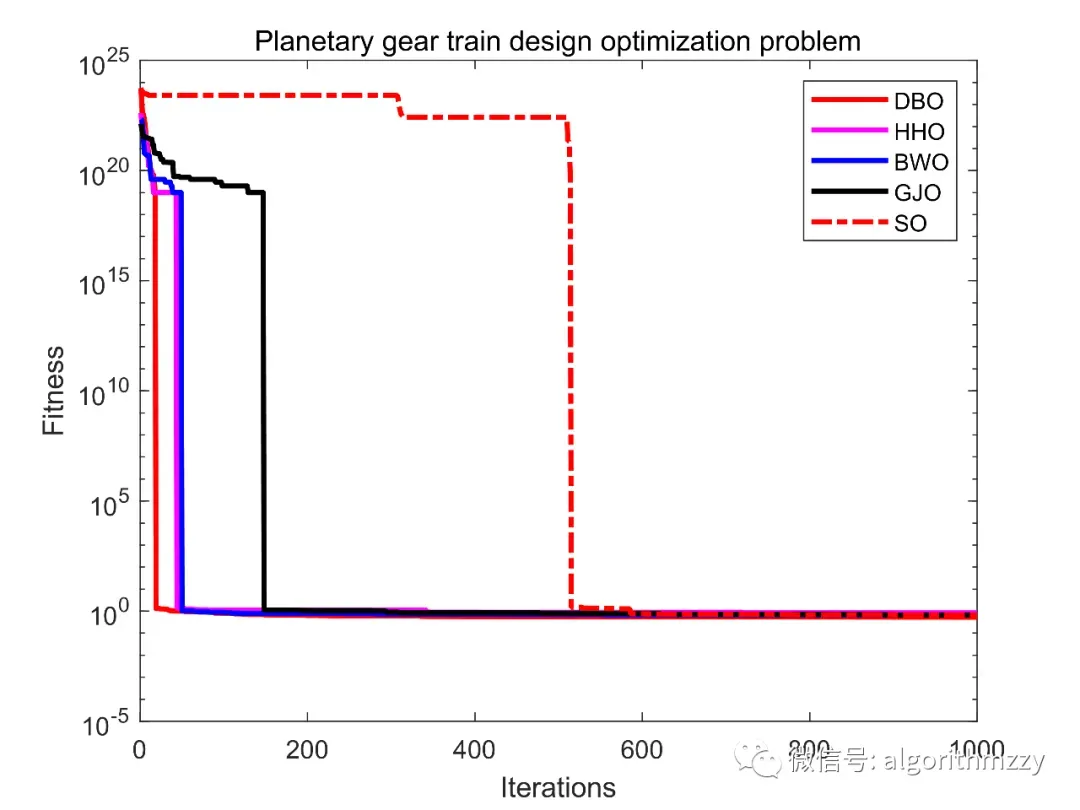
图9 Planetary gear train design optimization problem

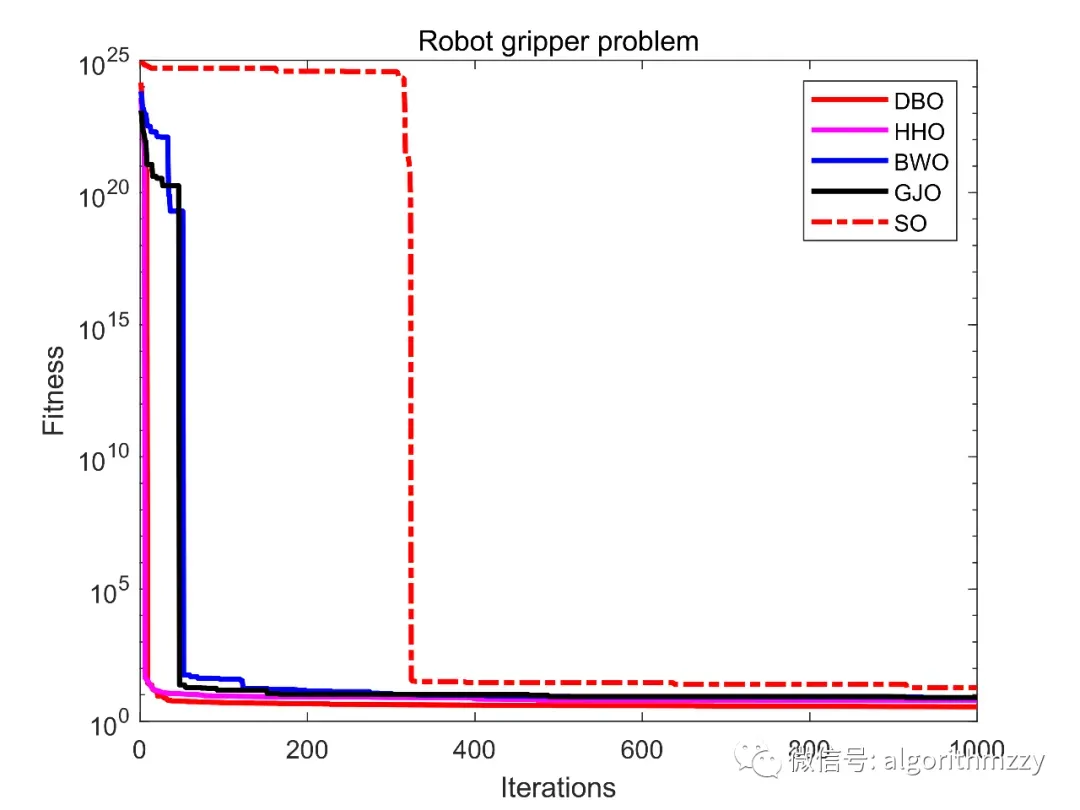
图12 Robot gripper problem

为了有更多的对比，以下这些近两年的文章也讨论了这些复杂的工程约束优化问题，可使用里面的数据做进一步对比，并且里面有更规范的数学描述：白冠鸡算法(COOT) [4]、变色龙算法(CSA) [5]、帝企鹅优化(AFO) [6]、非洲秃鹫优化算法(AVOA) [7]、金鹰优化(GEO) [8]、气体溶解度优化(HGSO) [9]、野狗优化算法(DOA) [10]……

04
MATLAB代码

MATLAB代码可通过复制下方链接进入获得，代码附有详细注释。其中，main.m是主函数，直接运行即可；DBO.m是算法的代码(其余对应的就是HHO.m、BWO.m、GJO.m和SO.m)；Problem_range.m是6个工程优化设计问题的基本性质，规定了问题的维度、各决策变量的取值范围；Problem_models.m是6个工程优化设计问题的数学模型，即目标函数、约束条件，以及使用罚函数处理约束的过程；Bound_limit.m是边界约束处理，保证解的决策变量不超出取值范围。

蜣螂优化(DBO)算法在工程优化设计中的应用(第2期)：

哈里斯鹰优化(HHO)算法在工程优化设计中的应用(第2期)：

白鲸优化(BWO)算法在工程优化设计中的应用(第2期)：

金豺优化(GJO)算法在工程优化设计中的应用(第2期)：

蛇优化(SO)算法在工程优化设计中的应用(第2期)：

（公众号里有，关注：启发式算法讨论）

05
参考文献

[1] Coello C A C. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: a survey of the state of the art[J]. Computer methods in applied mechanics and engineering, 2002, 191(11-12): 1245-1287.

[2] Dong, M., Wang, N., Cheng, X., & Jiang, C.: Composite differential evolution with modified oracle penalty method for constrained optimization problems. Mathematical problems in engineering, 2014, 1-15 (2014).

[3] 汪逸晖, 高亮. 乌鸦搜索算法的改进及其在工程约束优化问题中的应用[J]. 计算机集成制造系统, 2021, 27(07): 1871-1883.

[4] Naruei I, Keynia F. A new optimization method based on COOT bird natural life model[J]. Expert Systems with Applications, 2021, 183: 115352.

[5] Braik M S . Chameleon Swarm Algorithm: A Bio-inspired Optimizer for Solving Engineering Design Problems[J]. Expert Systems with Applications, 2021, 174(1):114685.

[6] Yang Z ,  Deng L B ,  Wang Y , et al. Aptenodytes Forsteri Optimization: Algorithm and applications[J]. Knowledge-Based Systems, 2021, 232:107483-.

[7] Abdollahzadeh B ,  Gharehchopogh F S ,  Mirjalili S . African Vultures Optimization Algorithm: A New Nature-Inspired Metaheuristic Algorithm for Global Optimization Problems[J]. Computers & Industrial Engineering, 2021, early:1.

[8] Mohammadi-Balani A , MD Nayeri,  Azar A , et al. Golden Eagle Optimizer: A nature-inspired metaheuristic algorithm[J]. Computers & Industrial Engineering, 2020, 152:107050.

[9] Hashim F A ,  Houssein E H ,  Mai S M , et al. Henry gas solubility optimization: A novel physics-based algorithm[J]. Future Generation Computer Systems, 2019, 101.

[10] Peraza-Vázquez H, Peña-Delgado A F, Echavarría-Castillo G, et al. A bio-inspired method for engineering design optimization inspired by dingoes hunting strategies[J]. Mathematical Problems in Engineering, 2021, 2021: 1-19.