匈牙利匹配先前在损失函数那块已经介绍过,但讲述了并不清晰,而且准确来说,匈牙利匹配所用的cost值与损失函数并没有关系,因此今天我们来看一下匈牙利匹配这块的代码与其原理。
前面已经说过,DETR将目标检测看作集合预测问题,在最后的预测值与真实值匹配过程,其实可以看做是一个二分图匹配问题,该问题的解决方法便是匈牙利算法。
首先我们来了解一下相关概念:
相关概念
集合预测
目标检测通常建模为集合预测问题,是将所有物体一起预测出来,而不像自回归模型(Autoregressive model,AR),需要一个一个物体进行预测,下一个物体依赖上一个物体预测结果。比如:DETR最后一张图片,真值有2个bounding box(框,简称:bbox),DETR中会固定预测出100个bbox框(预测的结果包含框的位置、大小以及框中目标具体类别),这些生成的bbox就是集合预测结果。集合预测在推理阶段如何给出推理结果?在训练阶段如何给出loss?
推理阶段:100个bbox集合在推理阶段通过0.7的阈值进行区分。大于阈值认为是前景图,也就是那几只海鸟,小于阈值bbox是no object 背景图。注意:预测的时候是将100个bbox同时预测出来的,不像自回归模型一个一个生成的。其实也有道理:预测左边那只海鸟并不需要右边那只海鸟预测的bbox,不同bbox没有逻辑上的关系需要建模。这里有个问题:推理阶段计算的什么结果>0.7?
训练阶段:真值有2个bbox,但是预测了100个bbox,怎样建模和计算这100个bbox和真值的loss?画个简图,方便说明。
如何匹配?
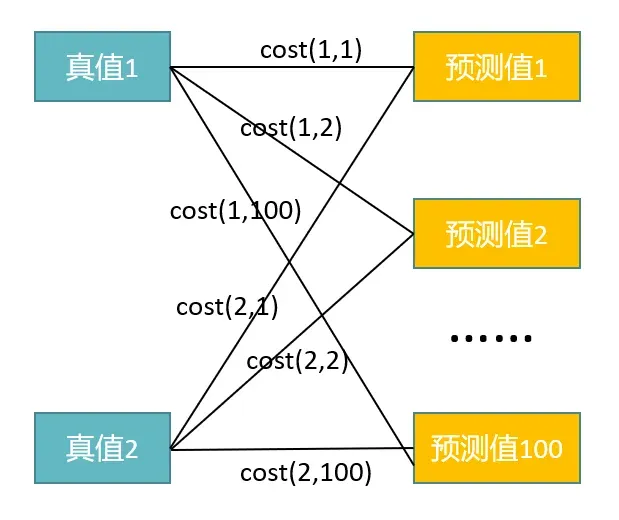
简单来说二分图:顶点是不相交的子集(真值集和预测集),每条边所依附的顶点分属于这2个子集,2个子集中的顶点不被线连接。
匹配:在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。
二分图匹配:找到一组边集合,这组边集合没有共同的顶点,举个例子:cost(1,1)和cost(2,100)是二分图匹配;cost(1,2)和cost(2,2)不是一个二分图匹配,因为其有共同依附顶点预测2。另外,cost可以组织成[2,100]的矩阵,匈牙利算法的输入就是这个矩阵,源码分析中会详细介绍。
二分图匹配
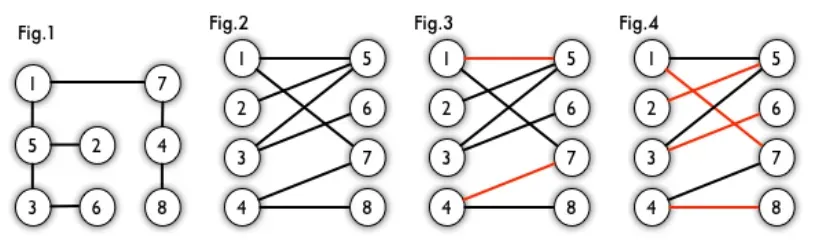
我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点,其他顶点为未匹配点;1-5、4-7为匹配边,其他边为非匹配边。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
举例来说:如下图所示,如果在某一对男孩和女孩之间存在相连的边,就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对,使得每对儿都互相喜欢呢?图论中,这就是完美匹配问题。如果换一个说法:最多有多少互相喜欢的男孩/女孩可以配对儿?这就是最大匹配问题。
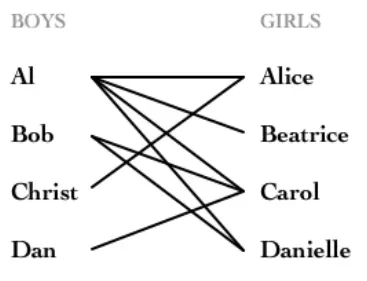
求解最大二分图匹配所用的算法便是匈牙利算法,那么该如何去做呢?
目标:找到预测值和真值cost最小的二分图匹配(找到满足条件的边集合),搜索算法是匈牙利算法。当然也可以不使用匈牙利算法,最简单的思路是将预测结果进行一个全排列 ,真值和前2个预测结果cost总和,进行全局比较,取出最小cost的排列情况。这个运算量并不低,耗时也比较长。
在学习匈牙利算法前,首先我们先来明确几个定义。
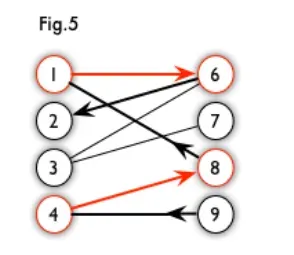
交替路:从一个未匹配点出发(右),依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路:从一个未匹配点出发(右),走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。
例如,图 5 中的一条增广路如图 6 所示(图中的匹配点均用红色标出):
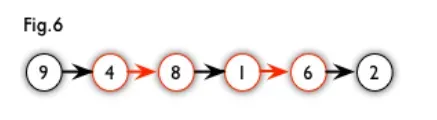
增广路有一个重要特点:非匹配边比匹配边多一条。因此,研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目比原来多了 1 条。
我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理)。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前,先讲一下匈牙利树。
匈牙利树
匈牙利树一般由 BFS 构造(类似于 BFS 树)。从一个未匹配点出发运行 BFS(唯一的限制是,必须走交替路),直到不能再扩展为止。例如,由图 7,可以得到如图 8 的一棵 BFS 树:(红色为匹配边)
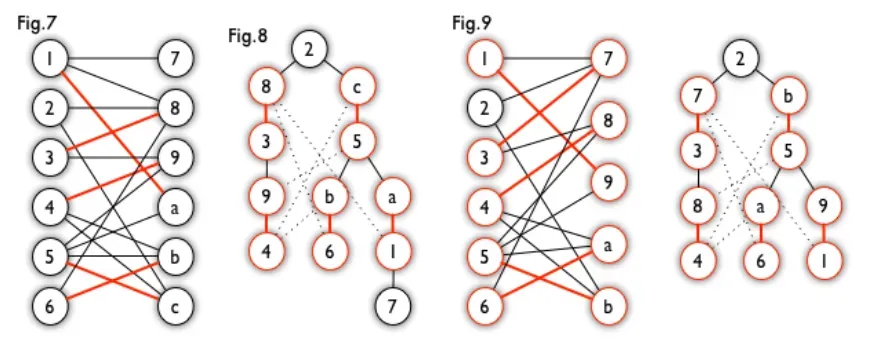
这棵树存在一个叶子节点为非匹配点(7 号),但是匈牙利树要求所有叶子节点均为匹配点(重点),因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点,那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示(顺便说一句,图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路,沿这条增广路扩充后将得到一个完美匹配)。
匈牙利树就是存在的可连接的匹配点都列出来(BFS)
最后再看一下由增广路径的定义可以推出的三个结论:
①P的路径长度必定为奇数,第一条边和最后一条边都不属于M,因为两个端点分属两个集合,且未匹配(单独的一条连接两个未匹配点的边显然也增广路径).
②P经过取反操作可以得到一个更大的匹配M
③M为G的最大匹配当且仅当不存在相对于M的增广路径
DETR中的匈牙利匹配
在DETR中使用匈牙利算法进行预测框与真实框的匹配是如何实现的呢,其实是pytorch已经给我们写好了接口,我们只需要将cost矩阵传入即可。这其实便是匈牙利算法应用中的指派问题,而稍有不同的是,对于匈牙利算法的标准型其适用的条件为:
- 目标函数求min;
- 效率矩阵为n阶方阵;
- 效率矩阵中所有元素Cij≥0,且为常数。
而在DETR模型中,很明显其构成的代价矩阵并不是个方阵,那么该如何解决呢?其实很容易,假设我们的真实框为20个,预测框为100个,那么就将真实框扩充到100,其代价阵用0填充即可。
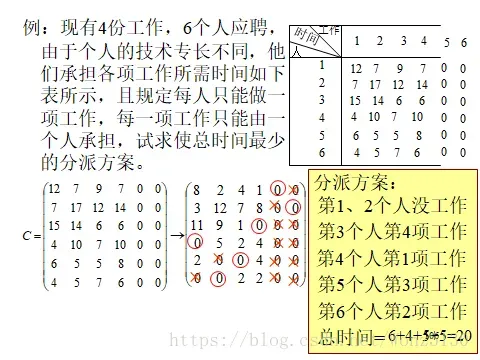
cost计算
cost计算又称为bipartite matching loss(其实是二分图匹配问题,之所以叫loss,可能是因为类似loss,需要找到cost最小的二分图匹配),使用匈牙利算法求解。注意:匈牙利算法找到的是和当前真值代价最小的预测结果,并不是最终loss。
bipartite matching loss公式:
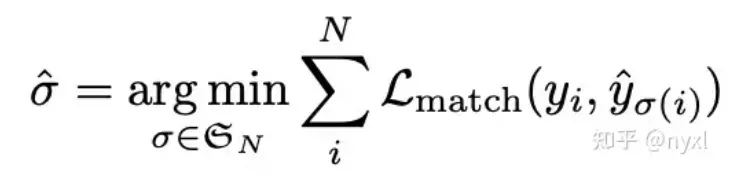
N 表示预测结果数量,DETR固定为100,其实也是object queries的数量,暂时先理解为固定值。
yi = (ci,bi) 表示真值,ci表示当前bbox图像类别;bi 表示bbox真值且有四个维度,分别是中心点的横纵坐标和bbox的宽、高。真值数量< N,假设真值有2个,为表达方便padding到100个,padding内容为 空集,理解成空就行。


真值和预测结果之间的cost应该如何计算?即 Lmatch
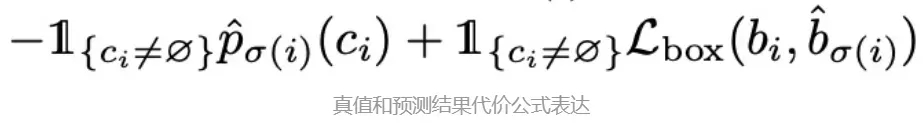


IoU(intersection of union,简单理解就是预测框和真值框的面积交集除以并集)。直观理解,bbox真值和预测结果的cost为L1 loss+IoU loss。为什么是这个组合?如果仅保留1个loss对结果有什么影响?
论文中用实验给出了解释:
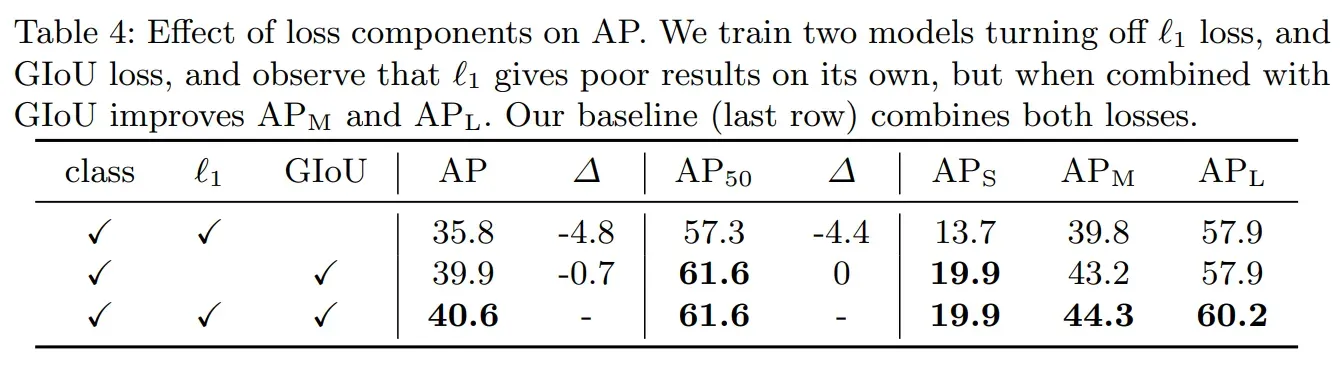
表格表示使用不同loss组合,AP值变化的情况。可以看到GIoU对最后结果的影响比L1大,尤其在小物体的识别上。综合来看,L1 loss+GIoU loss效果是最好的。为什么在L1 loss存在的情况下还需要增加GIoU?L1 loss比较适合回归任务,但是有个问题,随着bbox预测的结果越大,L1的值也越大,明显不是太合理,所以增加了一个IoU loss的惩罚,来降低预测bbox的大小带来的影响。如果不做这个惩罚,模型都会倾向预测出大框,这样模型收益(loss减少)最大,从而在大物体检测效果上会更好,所以这也是为什么去掉GIoU后,对小物体检查效果的影响比大物体高的原因。

计算出真值和预测结果的cost后,使用匈牙利算法求解,可以得到和真值cost最小的预测结果排列组合情况。再强调:这里仅仅是找到预测框,而并不是真正的loss。需要注意,在代码中分类的概率是不增加log的,因为这样2边的cost才能在同一个数量级下,为什么需要将不同的cost控制在同一个数量级下?可以想象分类的概率如果在100以上,而bbox的cost在10左右,那模型就会努力降低分类的loss,bbox的loss学习的并不会很好,预测类别准了,但是位置和大小不对,这也不是我们想要的。公式右边是预测结果和真值最小cost的表达,是通过匈牙利算法获取的。
算法解析
代码在models/matcher.py中
bs, num_queries = outputs["pred_logits"].shape[:2]
# We flatten to compute the cost matrices in a batch
out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1) # [batch_size * num_queries, num_classes]
out_bbox = outputs["pred_boxes"].flatten(0, 1) # [batch_size * num_queries, 4]
# Also concat the target labels and boxes
tgt_ids = torch.cat([v["labels"] for v in targets])
tgt_bbox = torch.cat([v["boxes"] for v in targets])
# Compute the classification cost. Contrary to the loss, we don't use the NLL,
# but approximate it in 1 - proba[target class].
# The 1 is a constant that doesn't change the matching, it can be ommitted.
cost_class = -out_prob[:, tgt_ids]
# Compute the L1 cost between boxes
cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1)
# Compute the giou cost betwen boxes
cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox), box_cxcywh_to_xyxy(tgt_bbox))
# Final cost matrix
C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou
C = C.view(bs, num_queries, -1).cpu()
sizes = [len(v["boxes"]) for v in targets]
indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))]
return [(torch.as_tensor(i, dtype=torch.int64), torch.as_tensor(j, dtype=torch.int64)) for i, j in indices]
输入outputs结构
这里的outputs即DETR模型的输出结果,其经过了预测头输出后的到的维度为:【2,100,7】,【2,100,4】
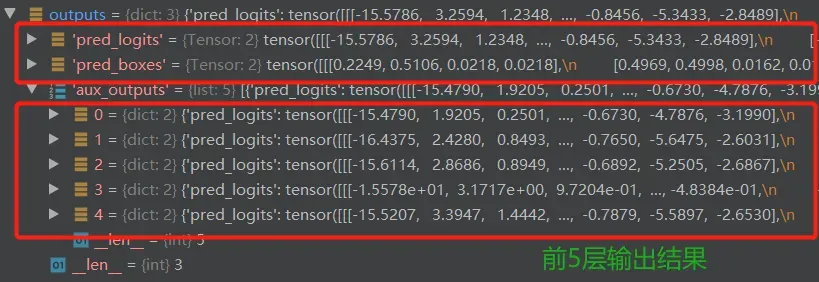
pred_logits:图片类别预测结果。维度=[2,100,7],数据集中图片共有6个类别+1(无类别),object queries大小设置为100(也就是总共100个框),batch_size=2(本地debug,内存有限见谅)。pred_logits为object queries预测图片类别结果分布向量。
pred_bbox,预测bbox结果。维度=[2,100,4],每个bbox为4维向量(中心点的二维坐标和图片的宽和高),object queries的大小设置100,batch_size=2。也就是说,pred_bbox为object queries预测的bbox结果。
预测结果和真值结构重构
bs为batch_size大小,num_queries为预测框数量(源码中设定的是100)。
bs, num_queries = outputs["pred_logits"].shape[:2]
out_pred,类别预测向量去掉batch维度,维度=[200,7],后面接softmax,获取所有batch中object queries预测类别分布情况,注意这里没有计算交叉熵,所以这里不是计算loss,而是cost(距离)。
out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1)
out_bbox,bbox预测结果去掉batch维度,维度=[200,4]。object queries预测的结果框,每个batch固定设置100个框,2个batch就预测出200个框。
out_bbox = outputs["pred_boxes"].flatten(0, 1)
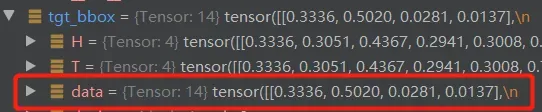
tgt_id:图片类别真值,维度=[14]。总共2张图片,第一张图片13个物体,第二张图片有1个物体,所以concat有14维。
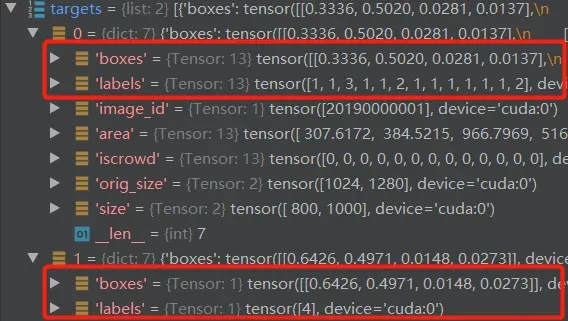
tgt_ids,真值框对应类别id编号
tgt_ids = torch.cat([v["labels"] for v in targets])
tgt_ids:tensor([1, 1, 3, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 4], device='cuda:0')
tgt_bbox:图片框真值,维度=[14,4]。与out_bbox对应。
tgt_bbox = torch.cat([v["boxes"] for v in targets])
类别损失计算:
cost_class = -out_prob[:, tgt_ids]
这里开始时博主没有明白其意思,原来是其损失公式发生了变化,我们来捋一捋。
首先out_prob为【200,7】,其内为200个框中对7个类别的预测概率值,tgt_ids为真值中的类别id,此时他是使用这个id去取所有预测该类别的概率值
out_prob结构如下:
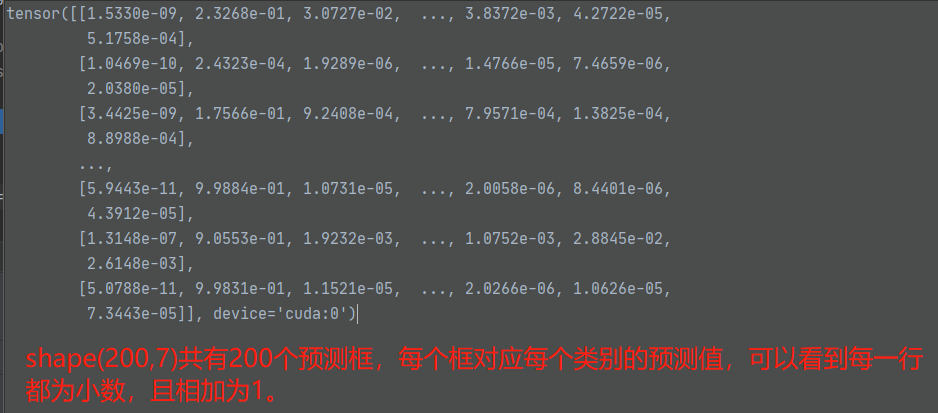
最终得到cost_class的shape为【200,14】,即每个真值类别都的到了这200个框的预测值,例如在第一个真值类别的cost_class中有200个框的预测,原本用1-预测该类为其损失,但1是一个常数,也就无关紧要,这也是为何out_prob前有个负号的原因。最终的cost_class内部的值也都为负数。
分类和bbox cost
cost_class:cost_class获取out_pred中tgt_id对应的图片类别
预测概率,表示分类预测结果的代价,维度=[200,14]。类别cost没有和目标值计算loss。具体来说,out_pred总共有200个框,每个框都有这7个类别上的概率分布,cost_class =-out_prob[:, tgt_ids]将每个框在这14个类别标签上的预测结果取出来,构建出分类的cost。这个理解很重要,需要理解为什么维度是[200,14],这也正好对应公式:
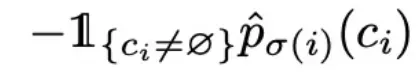
cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1)
cost_bbox:计算out_bbox和tgt_bbox的距离,维度=[200,4]。这两个数据维度并不相同,torch.cdis计算L1距离,也就是200个预测框和14个真值框两两计算L1距离,所以每一行表示的是当前预测框和14个真值框的L1距离。其shape为【200,14】


cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox), box_cxcywh_to_xyxy(tgt_bbox))
cost_giou:不用理解具体操作,维度=[200,14]。表示内容同上,唯一不同的是这里表示的是iou距离。
这里需要用到几个函数来将xywh转换为(x1,y1),(x2,y2)的形式
def box_cxcywh_to_xyxy(x):
x_c, y_c, w, h = x.unbind(-1)
b = [(x_c - 0.5 * w), (y_c - 0.5 * h),
(x_c + 0.5 * w), (y_c + 0.5 * h)]
return torch.stack(b, dim=-1)
计算giou距离的generalized_box_iou方法位于utils/box_ops.py文件中
def generalized_box_iou(boxes1, boxes2):
"""
The boxes should be in [x0, y0, x1, y1] format
Returns a [N, M] pairwise matrix, where N = len(boxes1)
and M = len(boxes2)
"""
# degenerate boxes gives inf / nan results
# so do an early check
assert (boxes1[:, 2:] >= boxes1[:, :2]).all()
assert (boxes2[:, 2:] >= boxes2[:, :2]).all()
iou, union = box_iou(boxes1, boxes2)
lt = torch.min(boxes1[:, None, :2], boxes2[:, :2])
rb = torch.max(boxes1[:, None, 2:], boxes2[:, 2:])
wh = (rb - lt).clamp(min=0) # [N,M,2]
area = wh[:, :, 0] * wh[:, :, 1]
return iou - (area - union) / area
二分图匹配结果计算
注意:这里获取的是二分图匹配结果,也就是从所有预测框中找到和真值cost最小的框的组合情况,不是模型需要梯度下降的loss。
C为不同类别的cost分别赋予了一个系数(cost_bbox=5,cost_class=1,cost_iou=2),维度=[200,14]。再还原batch维度= [2,100,14]。这里对应的是cost矩阵,表示每个预测框(object queries)对应真值框的cost(距离),现在的目标是找到预测框和真值框cost最小的排列组合情况。
以上描述通过以下代码实现:
即将刚刚得到的cost_class,cost_bbox,cost_giou按照一定比例权重组合起来构成cost矩阵。
C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou
再次将cost矩阵转换为【2,100,14】形式
C = C.view(bs, num_queries, -1).cpu()
最后将cost送入执行匈牙利匹配过程:
sizes = [len(v["boxes"]) for v in targets]#shape:[13,1]
indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))]
linear_sum_assignment:传入的是代价矩阵C。因为第1张图真值有13个框,所以C矩阵第一列,维度=[2,100,13],C矩阵第二列,维度=[2,100,1](这里的7值得是框的个数,而非类别)。为什么要这样取数据?假设去掉batch维度,那么C矩阵被分解为[200,13]和[200,1],也就是200个object queries和前13个真值框的cost矩阵、200个object queries和后1个真值框的cost矩阵。而实际上应该是不同的100个object querie分别与13个,1个真实框的cost矩阵才对。
indices:表示匈牙利算法计算的最优匹配结果看懂这个结果很重要!
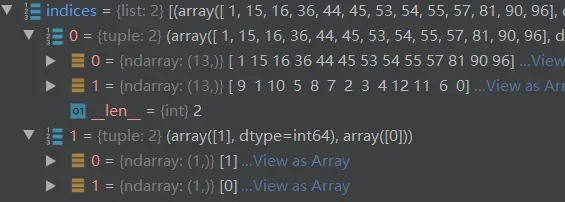
解释一下结果表示什么,一个batch中有2个sample,每个sample里固定有100个object query,以第二张图片为例,(array([1]), array([2]))对于第2个sample,编号为1的object query筛选出cost最小真值框是0号;同理对于第一个sample也是一样一一对应的,这个结果用在后面计算loss上。注意:每个真值框都能不重复的匹配一个object query,当真值数量<object queries 数量时,没有匹配上真值框的是模型认为的背景图;当真值数量> object queries数量,有些真值就无法匹配上object query。
此外,关于匈牙利匹配的实现过程,我们这里只是给出了cost矩阵的构造,完成预测框与真实框的匹配则是直接调用了linear_sum_assignment方法,该方法是官方封装好的,位于scipy.optimize之中,且该算法的输入代价矩阵可不为方阵。即scipy匈牙利算法的函数名为:scipy.optimize.linear_sum_assignment,该方法的输入参数为cost矩阵(一个array数组),返回值有两个分别是row_index,col_index,代表匹配值。
我们来看看其具体实现:
linear_sum_assignment
首先是矩阵array化
cost_matrix = np.asarray(cost_matrix)
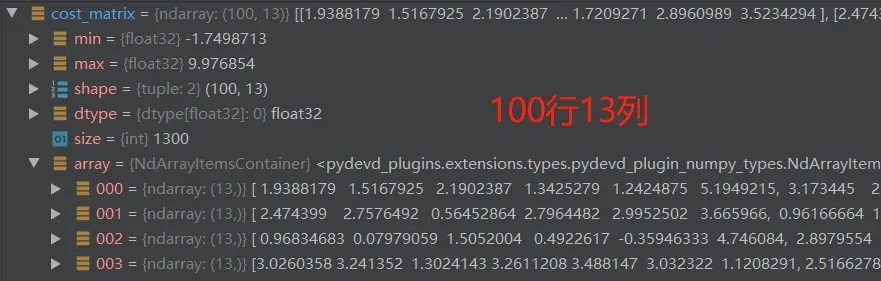
判断其是否为2维的,因为代价矩阵必须是2维的。
if len(cost_matrix.shape) != 2:
raise ValueError("expected a matrix (2-D array), got a %r array"
% (cost_matrix.shape,))
随后由单精度转为双精度后求最小值,并取出较小的那个维度并生成addary。
cost_matrix = cost_matrix.astype(np.double)
a = np.arange(np.min(cost_matrix.shape))
#a=[ 0 1 2 3 4 5 6 7 8 9 10 11 12]
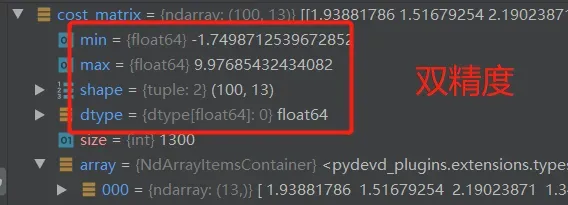
# The algorithm expects more columns than rows in the cost matrix.
if cost_matrix.shape[1] < cost_matrix.shape[0]:
b = _lsap_module.calculate_assignment(cost_matrix.T)
#b:[96 15 53 54 55 36 90 45 44 1 16 81 57]
indices = np.argsort(b)
#indices:[ 9 1 10 5 8 7 2 3 4 12 11 6 0]
return (b[indices], a[indices])
else:
b = _lsap_module.calculate_assignment(cost_matrix)
return (a, b)
代码注释中提到其想要让列的数量比行多。因此若是出现行比列多的情况,如现在,就要进行一个矩阵转置,随后再进行计算。最终输出indices

如此便完成了匹配过程了。
值得注意的是,匈牙利匹配过程说不更新梯度的,这在代码的forward中也有体现。

文章出处登录后可见!
