时间序列信号处理（一）—–变分模态分解（VMD)

1.简述变分模态分解

变分模态分解–vmd，适用于非线性时间序列信号，主要是利用求解变分问题的思想去对信号进行提取，在不丢失原始信号特征的情况下，把一个原始信号分解成多个不同中心频率的信号，即不在同一个调制信号内。

2.以轴承信号为例

安装vmd库，直接pip install vmdpy 即可

import matplotlib.pyplot as plt
import numpy as np
from vmdpy import VMD

读取信号

ball_18_0 = np.loadtxt('E:/12k1/0HP/inner18.txt')
data = ball_18_0[2048*2:2048*3]

设置参数，但分解层数K和二次惩罚系数α需要仔细考虑设定，特别是K值，对分解效果影响巨大。

# 参数设置
alpha = 2000      # moderate bandwidth constraint
tau = 0.            # noise-tolerance (no strict fidelity enforcement)
K = 5            # 3 modes
DC = 0             # no DC part imposed
init = 1           # initialize omegas uniformly
tol = 1e-7

u, u_hat, omega = VMD(data, alpha, tau, K, DC, init, tol)

绘制分解信号图

plt.figure(figsize=(10, 8))
for i in range(K):
    plt.subplot(K+1, 1, 1)
    plt.plot(data)
    plt.title("outer")
    plt.subplot(K+1, 1, i+2)
    plt.plot(u[i, :], linewidth=0.2, c='r')
    plt.ylabel('u{}'.format(i + 1))
plt.tight_layout()
plt.show()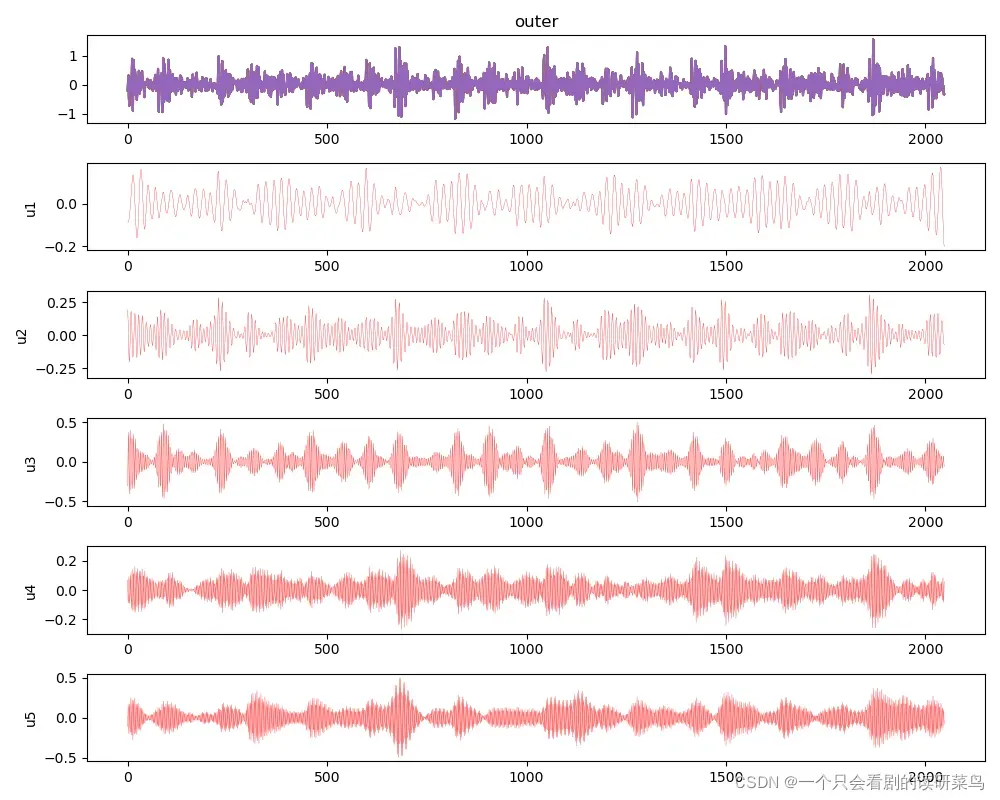

 最后绘出其频谱图

Fs = 12000
Ts = 1.0/Fs
t = np.arange(N)
k = np.arange(N)
T = N/Fs
frq = k/T
frq1 = frq[range(int(N/2))]


lt.figure(figsize=(10, 8))
for i in range(K):
    plt.subplot(K + 1, 1, 1)
    data_f = abs(np.fft.fft(data)) / N
    data_f1 = data_f[range(int(N / 2))]
    plt.plot(frq1, data_f1)
    plt.title("outer")
    plt.subplot(K+1, 1, i + 2)
    data_f2 = abs(np.fft.fft(u[i, :])) / N
    data_f3 = data_f2[range(int(N / 2))]
    plt.plot(frq1, data_f3, 'red')
    plt.xlabel('pinlv(hz)')
    plt.ylabel('u{}'.format(i + 1))
plt.tight_layout()
plt.show()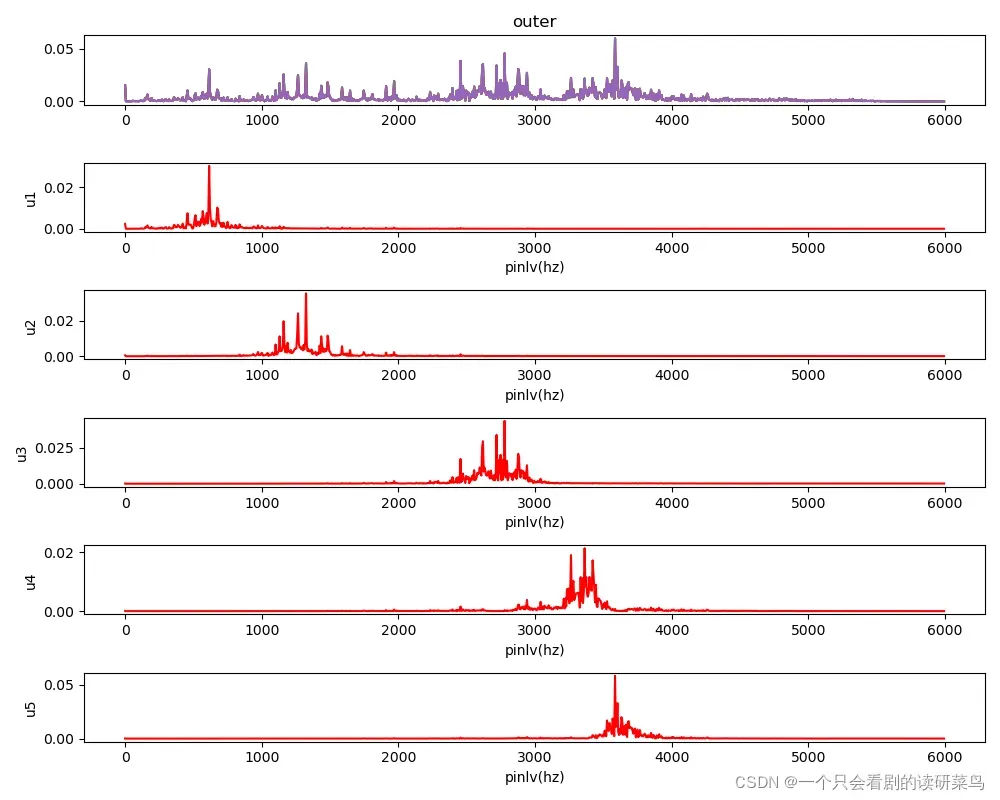

 由上述结果可知，分解出来的信号基本上不在同一个频率段，分解效果很好。