前言

NeRF从2020年发展至今，仅仅三年时间，而Follow的工作已呈井喷之势，相信在不久的将来，NeRF会一举重塑三维重建这个业界，甚至重建我们的四维世界（开头先吹一波）。NeRF的发展时间虽短，有几篇工作却在我研究的领域开始呈现万精油趋势：
* PixelNeRF-—泛化法宝
* MipNeRF—-近远景重建
* NeRF in the wild—-光线变换下的背景重建
* Neus—-用NeRF重建Surface
* Instant-NGP—-多尺度Hash编码实现高效渲染

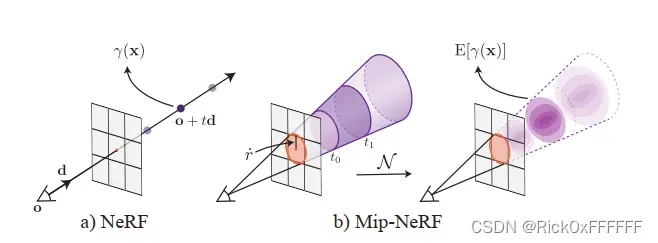
Abstract

由于远景近景的分辨率不同，导致经典NeRF对于多尺度场景的表达存在明显瑕疵：NeRF对于近景的重建比较模糊而对于远景的重建出现锯齿。简单粗暴的策略是supersampling，但是费时费力。相较于NeRF使用的位置编码（PE）方式，Mip-NeRF提出了积分位置编码的方式（IPE）.这种编码方式可以多尺度地描述空间中的信息分布，make sense.

NeRF

Positional Encoding:

$\gamma (x)=[\sin (x),\cos (x),...,\sin (2^{L-1}x),\cos (2^{L-1}x)]^T$

MLP:

$\forall t_k \in \mathbf{t}, [\tau_k,\mathbf{c}_k]=MLP(\gamma(\mathbf{r}(t_k);\Theta)$

Final Predicted Color of the Pixel:

$\mathbf{C}(\mathbf{r};\Theta,\mathbf{t})=\sum_{k}T_{k}(1-\exp(-\tau_k(t_{k+1}-t_k)))\mathbf{c}_k \newline with, T_k=exp(-\sum_{k'<k}\tau_{k'}(t_{k+1}-t_k))$

Loss Function：

$\min_{\Theta^c,\Theta^f} \sum_{r\in R}(\Vert C^*(r)-C(r;\Theta^c,\mathbf{t} ^c) \Vert^2_2+ \newline \Vert C^*(r)-C(r;\Theta^f,sort(\mathbf{t} ^c \cup \mathbf{t}^f )) \Vert^2_2)$

其中 $\mathbf{t}^f$ 是根据coarse modelinferene出的 $\omega_k=T_k(1-\exp(-\tau_k(t_{k+1}-t_k)))$ 经过inverse transform sampling求解出的。

Mip-NeRF

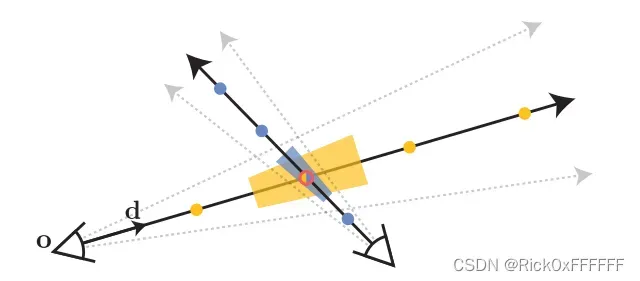
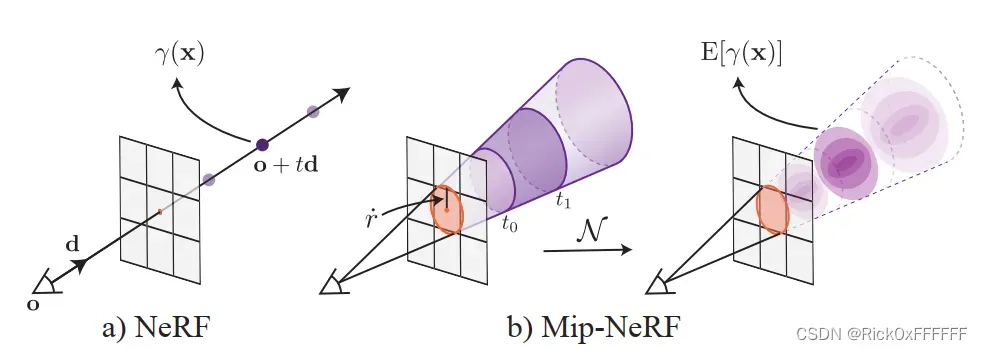
NeRF通过point-sampling的方式对每个像素–>所对应的射线进行位置编码，而忽略了每个采样点所包含的Shape, Volume等信息。

这导致了图中所示交汇处的黄点与蓝点会inference出相似的point-sampled feature. Mip-NeRF企图对Shape, Volume进行编码解决NeRF这一困境。

MipNeRF对一段ray所代表的锥台区域的定义如下:

红框部分图示如下：

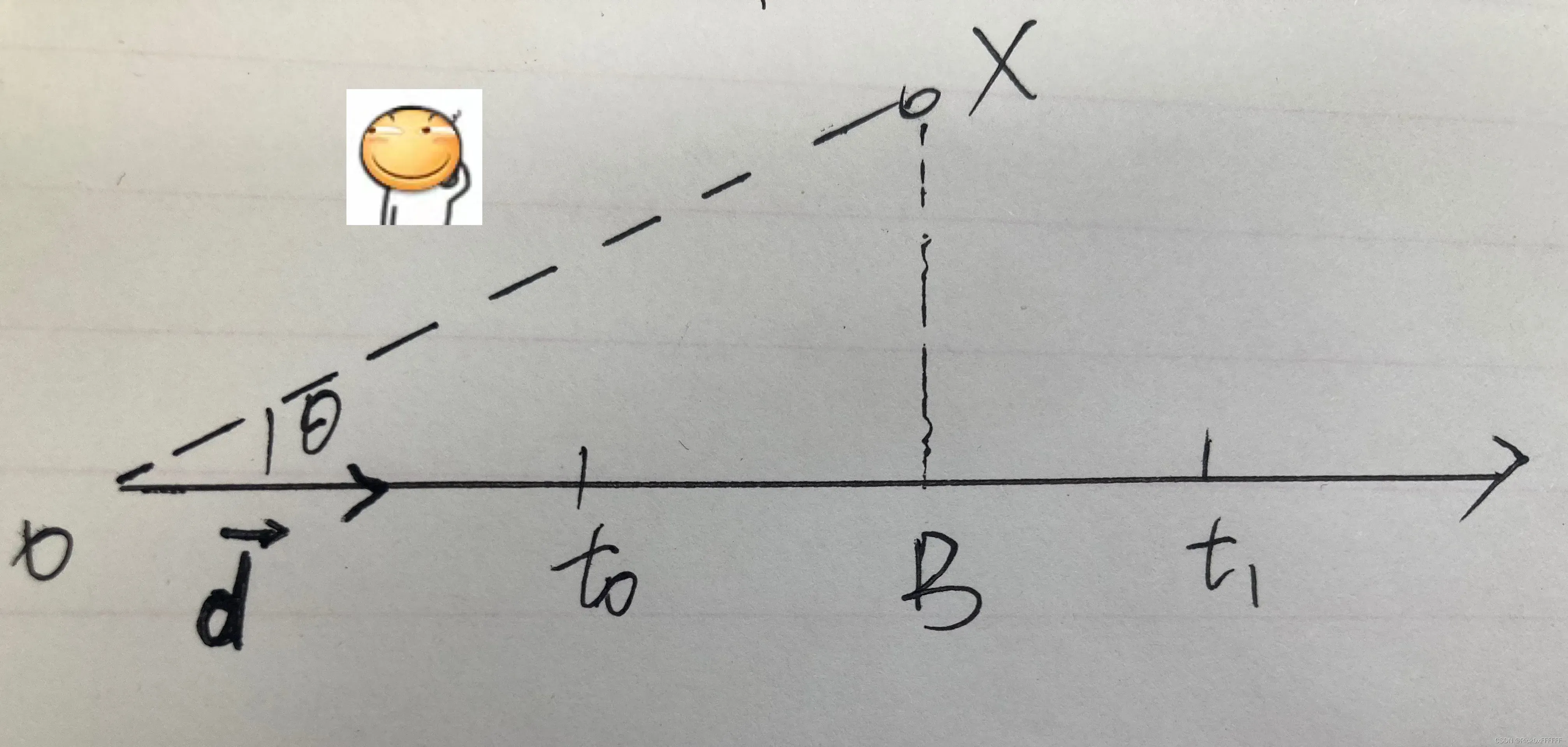
OB即为红框中间部分求解结果，在 $[t_0,t_1]$ 之间

$\theta_0,\theta_1$ 分别代表蓝框右式和左式。

期望位置编码为：

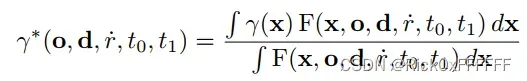
但这个公式没有闭式解，作者转而利用多元高斯求近似值，那就是求解 $(\mathbf{\mu},\mathbf{\Sigma})$ . 因为锥台是关于ray对称的，因此期望值应该在ray上，关于期望position,只需要求解ray上的期望distance，令其为 $\mathbf{\mu}_t$ . 以及沿ray线的 $\sigma^2_t$ ,以及垂直于ray的圆面所对应的 $\sigma^2_r$ .

先给结论，公式推导见公式推导章节：

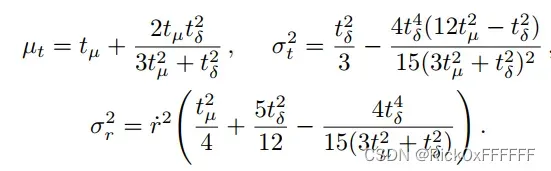
将均值与方差从锥台坐标系转换到世界坐标系下：

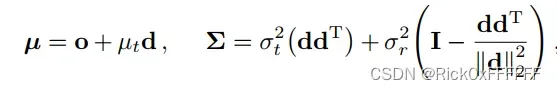
进行Positional Encoding, 令:

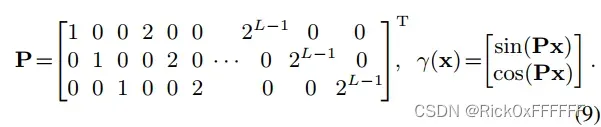
and

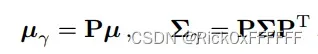
根据下式可求解IPE闭式解：

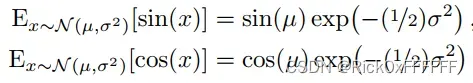
最后得到的IPE编码为：

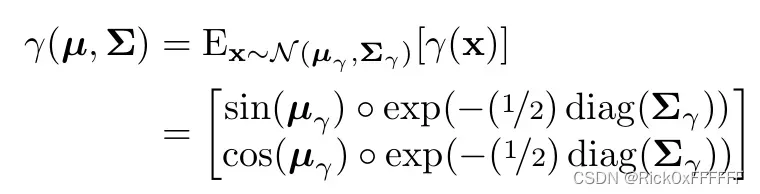
公式推导：

下面来说（ $\mathbf{\mu}_t$ , $\sigma^2_t$ , $\sigma^2_r$ )分别是怎么求解的

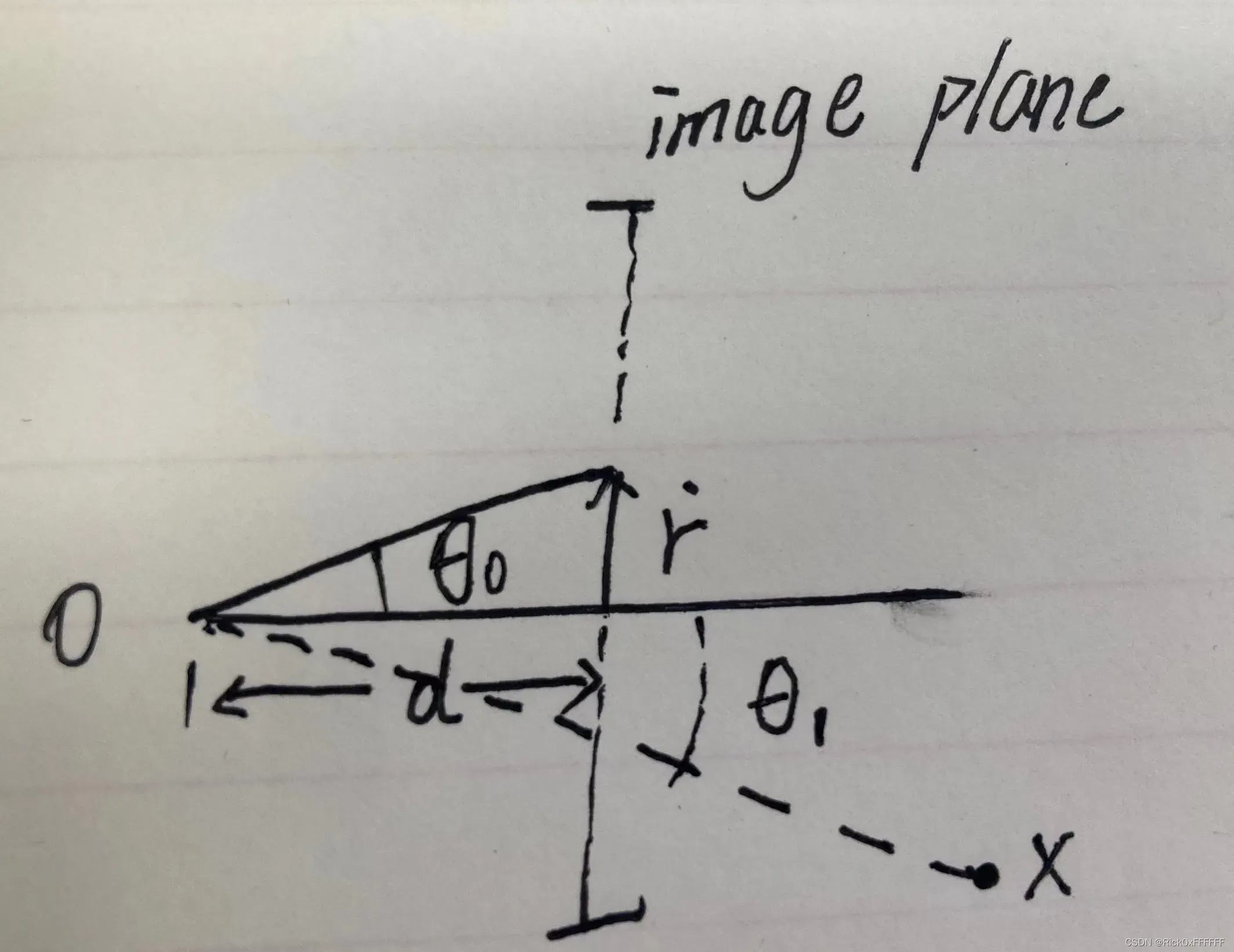
作者在supplement里面给出了推导过程，以下结合推导过程进行一些说明

$(x,y,z)=\varphi(r,t,\theta)=(rt\cos \theta,rt\sin \theta,t), \theta \in [0,2\pi), t\geq 0. \Vert r \Vert \leq \dot{r}$

此公式中需注意的是， $t$ 是一个关于原点到成像平面像素中心的距离 $d$ 的比例系数（这句话有点绕，见下图）

所以说，当 $t=1,r=\dot{r}$ 时，x和y就在刻画该像素的红色圆圈上。同理，当 $t=1,r\leq \dot{r}$ 时，该区域就是描述像素平面上该红色圆圈以内区域。为了求解锥台的三维积分，我们需要求解出描述三维空间的微分，如下所示：

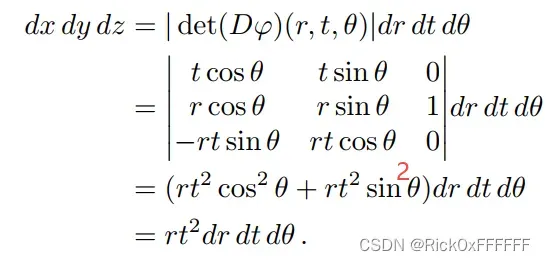
因此，锥台内的体积

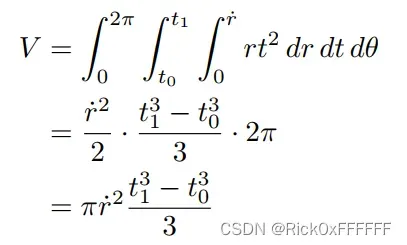
$t$ 的期望为：

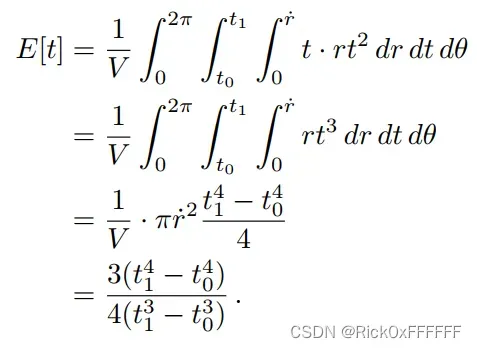
$t^{2}$ 的期望为：

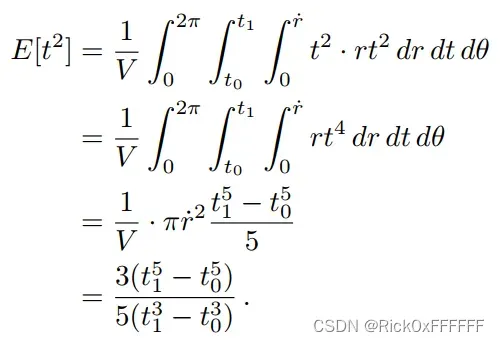
$x^2$ 的期望为：

$\mu_t=E(t)$ :

$\sigma^2=E(t^2)-E^2(t)$

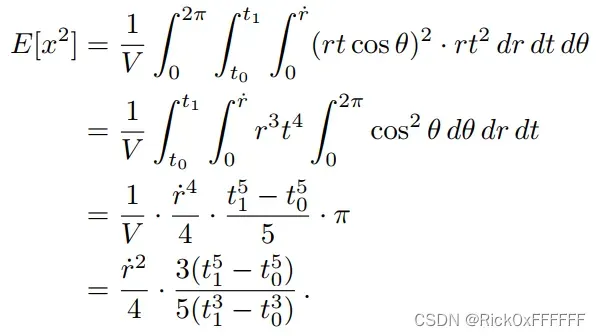
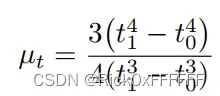
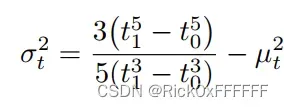
文章中说r的方差可以用x的或者y的来代替，这个是为啥我还需要再研究下，欢迎大佬们留言。

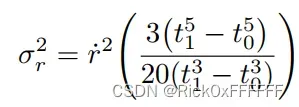
为了计算的稳定性，令 $t_1=(t_0+t_1)/2, t_{\delta}=(t_1-t_0)/2$ ，将上式经过等式变换后得到：

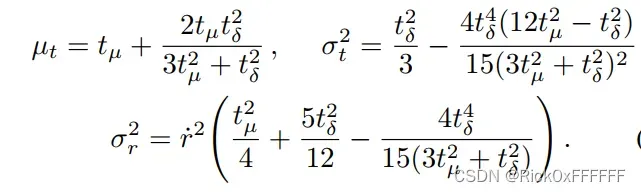
参考文献：

Barron, Jonathan T., et al. “Mip-nerf: A multiscale representation for anti-aliasing neural radiance fields.” Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021.

Barron, Jonathan T., et al. “Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields Supplemental Material.”

文章出处登录后可见！

已经登录？立即刷新

NeRF必读：Mip-NeRF总结与公式推导

前言

Abstract

NeRF

Mip-NeRF

公式推导：

相关推荐