终于肝完了!有一说一,这一次难度肉眼可见的提升,终于明白程序员为什么会秃顶了(头发真的禁不住薅啊),祝大家好运!
第1关:循环结构-while与for循环
第1题 编程计算如下公式的值1^2+3^2+5^2+…+995^2+997^2+999^2并输出结果
第2题 用while语句完成程序逻辑,求如下算法可以求根号x的近似值。(例如,x为3时,算法输出约为1.7320508)。
算法如下:
-
输入
x,若x为负数,则输出“无实数解”,算法结束; -
令
g=x/2; -
通过如下公式计算误差值,如果
∣x−g∗g∣<10−6,输出g,算法结束; -
否则,将
(g+x/g)/2作为新的猜测值,仍记为g。 -
重复步骤3和4
第3题:
用for循环完成下列程序,计算3位数的水仙花数 水仙花数是三位整数,且各位数字的立方之和等于该数,比如,因为
![]()
所以153是水仙花数。
第一关还是简单的热热身,熟悉for与while的基本用法,下一关!
from math import *
########## 第1题 ##############
i = 1 # 当前计算的值
s = 0 # 计算出来的和
# 第1题
########### begin ##########
while i<1000:
s += i**2
i=i+2
######### end ####
print(s)
########## 第2题 ##############
x = int(input())
if x<0:
print('无实数解')
else:
g = x/2
#######begin##############
# 请输入while循环控制语句
while abs(x-g*g)>pow(10,-6):
g=(g+x/g)/2
#######end#################
print("%.4f" %g)
########## 第3题 ##############
#计算并输出三位数内的水仙花数
#判断一个三位数是否是水仙花数,如果是输出1,否则输出0
def isflower(x):
# 函数说明:
#参数 x为一个3位数
#返回值为1或0
####### Begin #########
a,b,c=x//100,x//10%10,x%10
t=(a**3)+(b**3)+(c**3)
if t==x:
return 1
else:
return 0
####### End ########
#函数调用求三位数内的水仙花数并输出
####### Begin #########
# 请在此输入for循环表达式
for i in range(100,1000):
if isflower(i)==1:
print(i)
####### End ########第2关:循环嵌套-特殊图形的输出
第1题:从键盘输入m行n列,在屏幕上输出m行n列的*行图案 例如输入6,7 输出为:

第2题:从键盘输入m行,在屏幕上输出m行的直角图案
例如输入:8 输出为:

第3题:从键盘输入m行,在屏幕上输出m行的等腰三角形图案
例如输入9 输出为:

第二关已经稍微有一点难度了,常规做法是从头到尾双重循环,当然,也可逃课:
例如,第一题也可以这么写:
m,n = eval(input())
print(('*'*n+'\n')*m)第二题也可以这么写:
n = eval(input())
for i in range(n):
print('*'*(2*i-1))接下来是双重循环的所有代码:
#第一题:从键盘输入m行n列,在屏幕上输出m行n列的*行图案
m,n= eval(input())
#请在下面编写代码
# ********** Begin ********** #
for i in range (0,m):
for j in range (0,n):
print('*',end='')
print('',end="\n")
# ********** End ********** #
#第二题:从键盘输入m行,在屏幕上输出m行的直角图案
m=eval(input())
#请在下面编写代码
# ********** Begin ********** #
for i in range (0,m):
for j in range (0,2*i+1):
print('*',end='')
print('',end="\n")
# ********** End ********** #
#第三题:从键盘输入m行,在屏幕上输出m行的等腰三角形图案,试着用函数的方式来实现图形的绘制
def drawPic(n):
#函数说明
#参数n代表图案的行数
#函数无返回值
#请在下面编写代码完成
# ********** Begin ********** #
for i in range (0,m):
for j in range (0,m-i-1):
print(' ',end='')
for j in range (0,2*i+1):
print('*',end='')
print('',end="\n")
# ********** End *********** #
m=eval(input())
drawPic(m)第3关:循环综合-特殊数问题
第1题-斐波那契数列
在数学上,斐波那契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n – 1)+F(n – 2)(n ≥ 3,n ∈ N*)斐波那契 请完成求第n项斐波那契数的程序并输出结果 输入输出格式如下: 输入:5 输出:5
第2题-条件数的显示
用while语句完成程序,输出0至N之间的所有同时为2、3和5的倍数的数。 输入输出格式如下:用空格作为分隔符 输入:100 输出:0 30 60 90
第3题-素数问题
完成程序,输出输出0至N之间的素数。 输入输出格式如下:用空格作为分隔符
输入:10 输出:2 3 5 7
第4题-最大公约数与最小公倍数
完成程序,求最大公约数计算。从键盘接收两个整数,编写程序求出这两个整数的最大公约数和最小公倍数。(最大公约数可用辗转相除法求,最小公倍数则用两数的乘积除以最大公约数) 输入输出格式如下: 输入:12,18 输出: 最大公约数:6 最小公倍数:36
第三关对我们的数学提出了要求。第一题斐波那契数列,如果用F(n)=F(n – 1)+F(n – 2)(n ≥ 3,n ∈ N*)来直观表达,我们可以用列表递归的方式表达:
#用递归的方法,加上for循环,把每次循环产生的新项增加到数列最后,最后一次性输出list
def fubonacci3(n):
list = []
for i in range(n):
if i == 0 or i == 1:
list.append(1)
else:
list.append(list[i-2] + list[i-1])
return list
而最简单的方式就是不断的两个变量同时赋值,形成斐波那契数列。
第五题就是从小到大不断的寻找公约数,然后不断的赋值给它,当它不再被赋值时就是最大公约数
#第一题
#定义一个求第n项斐波那契数的函数
def fibNumber(n) :
#函数说明
#参数n为第n项斐波那契数,第1,2项为1,1
#返回第n项值
#********** Begin ********** #
a,b = 0,1
for i in range (n):
a,b = b,a+b
return a
#********** End ********** #
#请不要修改下面的代码
m = int(input())
print(fibNumber(m))
print(20*'*'+'\n',end='')
#第二题:可试着用非函数的方式写程序,注意输出数据格式
n =eval(input())
# 请在下面编写代码
# ********** Begin ********** #
i=0
while i<=n:
if i%5==0 and i%3==0 and i%2==0:
print (i,end=' ')
i=i+10
# ********** End ********** #
print('\n'+20*'*'+'\n',end='')
#第三题
#定义一个判断x是否是素数的程序
def isPrime(x):
#函数说明:
#参数x为>=2的整数
#返回值为1或0
# ********** Begin ********** #
for i in range(2,x):
if x%i ==0:
return 0
return 1
# ********** End ********** #
# 请不要修改下面的代码
N = int(input())
#求0-N之间的素数并输出,注意数据的输出格式
# ********** Begin ********** #
for i in range (2,N+1):
if isPrime(i)==1:
print(i,end=' ')
# ********** End ********** #
print('\n'+20*'*'+'\n',end ='')
#第四题
#定义一个求两个数的最大公约数的函数
def gcd(a,b):
#函数说明
#参数a,b为两个整数,并且a>b
#返回两个数的最大公约数
# ********** Begin ********** #
for i in range(1,max(a,b)+1):
if a%i==0 and b%i==0:
j = i
return j
# ********** End ********** #
# 请不要修改下面的代码
m,n = eval(input())
#函数调用求最大公约数保存在gcdnum中
# ********** Begin ********** #
gcdnum = gcd (m,n)
# ********** End ********** #
print("最大公约数:%d"% gcdnum)
print("最小公倍数:%d"%((m*n)/gcdnum))
print(20*'*',end='') 第4关:循环综合-数列问题
第1题—-求π/4
用循环的方式求π/4≈ 1-1/3+1/5-1/7+……直到最后一项绝对值小于le−6(即10−6)为止,结果保留小数点后10位
第2题—-数列和
完成程序,求:1-3!+5!-7!……(-1)n-1(2n-1)!,求前n的项的和。 输出格式如下: 输入:4 输出:数列前4项的和为-4925
第3题—-求sin(X)
完成程序,从键盘输入x的值,求
![]()
直到最后一项绝对值小于le−7(即10−7)为止(注:x为弧度值),结果保留小数点后10位。 说明:输入角度值,再转换成弧度值 输出格式如下: 输入:30 输出:output=0.4999999919
第四关 个人感觉第四关的难点在于初值的赋值以及while语句中的前后顺序,弄清楚了就如同砍瓜切菜。
#第1题:用循环的方式求π/4≈ 1-1/3+1/5-1/7+......直到最后一项绝对值小于1e−6(即10−6)为止,保留小数点后10位
import math
# ********** Begin ********** #
S=0
i=1
t=1
flag=1
while abs(i)>pow(10,-6):
S+=i
t+=2
flag=-flag
i=(1/t)*(flag)
# ********** End ********** #
# 请不要修改下面的代码
print("数列和为:%.10f" % S )
#0.7853986634
#第2题求:1-3!+5!-7!......(-1)n-1(2n-1)!,求前n的项的和
#函数定义求前n项数列和
def sumSequ(n):
#函数说明
#参数n为数列前n项
#返回前n项的和
# 请在下面编写代码
# ********** Begin ********** #
i=1;
t=1;
Sum=0;
flag=1;
while i<=n :
Sum=Sum+t*flag
i+=1
t=t*(2*i-2)*(2*i-1)
flag=-flag
return Sum
# ********** End ********** #
# 请不要修改下面的代码
m =int(input()) #从键盘输入 m值
s = sumSequ(m) #函数调用求数列和
print("数列前%d项的和为%d"%(m,s))
#第3题
from math import *
def calSinx(x):
#函数说明:
#参数x为弧度值
#返回数列和的结果,保留小数点后10位
#请在下面编写代码
# ********** Begin ********** #
S=0
i=x
t=1
while abs(i)>pow(10,-7):
S += i
t+=2
i=-(i*x*x)/((t-1)*t)
return S
# ********** End ********** #
# 请不要修改下面的代码
theta= eval(input()) #输入角度值
x =radians(theta)
Sx = calSinx(x)
print("output=%.10f"%(Sx)) 第5关:循环综合-天天向上的力量
任务一:俗语“三天打鱼两天晒网”,一年下来能力值又会是多少呢?请补全代码完成程序编写 #三天打鱼两天晒网 dayup, dayfactor = 1.0, 0.01
任务二:如果按工作日5天学习,周末2天休息每天相比前一天下降1%,工作日要努力到什么程度,一年后的水平才能与每天努力1%取得的效果一样呢?请补全代码完成程序编写。以0.001为dayfactor的增量值。
任务三:尽管每天坚持,但人的能力发展并不是无限的,它符合特定模型,假设能力增长符合以下模型:以7天为一周期,连续学习3天能力值不变,但从第4天开始至第7天每天能力增长为前一天的1%,如果7天中有一天间断学习,则周期从头计算,请编写程序,如果初始能力为1,固定每10天休息一天, 365天后能力值是多少,请补全代码完成程序编写。
第五关 终于来到了最后一关,这一关绝对是我目前遇到的最难一关。先不说绕来绕去的逻辑,光是这大段的文字已经能让人头痛一会了,这题光是题干我都读了半个小时。我来帮大家梳理一下:
任务一:做三休二,效率固定,较为简单
任务二:做五休二,这里注意工作日的工作效率为变量,而休息日的遗忘效率为不变量,注意区别。变量范围记得一定是小于等于而非直接等于,可能有微小误差导致循环停不下来。
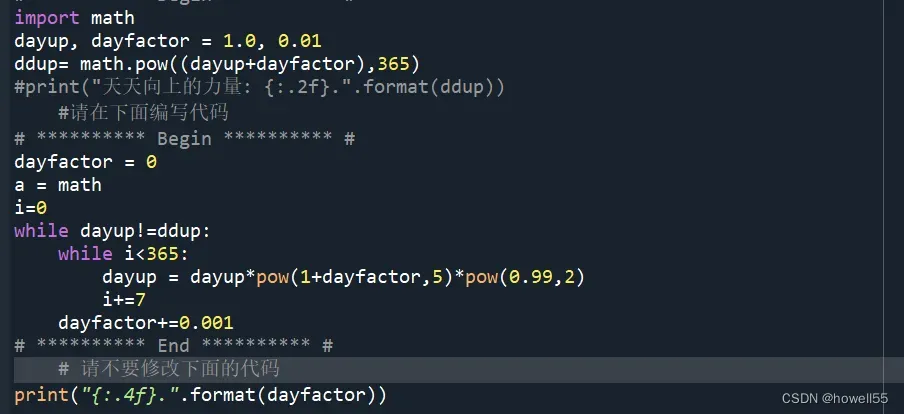
上面是错误示范!!!双重循环+等于才停止的双重buff直接给CPU干烧了!
任务三:做九休一,又遇到每七天一个轮回,通俗的来说遇到七的倍数与十的倍数都要避让,虽然这题这样做做对了,但是我还是有一个疑问,休息的时候不会遗忘吗?![]()
from math import *
#任务一:三天打鱼两天晒网
dayup, dayfactor = 1.0, 0.01
#请在下面编写代码
# ********** begin ********** #
i=0
while i<365:
dayup = dayup*pow((1+dayfactor),3)*pow((1-dayfactor),2)
i+=5
# ********** End ********** #
# 请不要修改下面的代码
print("{:.2f}.".format(dayup))
#任务二:天天向上的力量
import math
dayup, dayfactor = 1.0, 0.01
ddup= math.pow((dayup+dayfactor),365)
#print("天天向上的力量: {:.2f}.".format(ddup))
#请在下面编写代码
# ********** Begin ********** #
def dayup(df):
dayup = 1
for i in range(365):
if i % 7 in [6, 0]:
dayup = dayup * (1 - 0.01)
else:
dayup = dayup * (1 + df)
return dayup
dayfactor = 0.01
while dayup(dayfactor) <= ddup:
dayfactor += 0.001
# ********** End ********** #
# 请不要修改下面的代码
print("{:.4f}.".format(dayfactor))
#任务三:天天向上续
from math import *
Restday = 10 #休息10天,
dayup, dayfactor = 1.0, 0.01 #初始值
#请在下面编写代码
# ********** Begin ********** #
for i in range(365):
if 0<i%10<=3 or 0<i%7<=3:
dayup=dayup
else:
dayup=1.01*dayup
# ********** End ********** #
# 请不要修改下面的代码
print("{:.2f}".format(dayup))#文章出处登录后可见!
