目录
引言
数据格式
运行代码
Holt-Winters模型主体
程序入口
参数讲解
开始训练
预测结果
引言
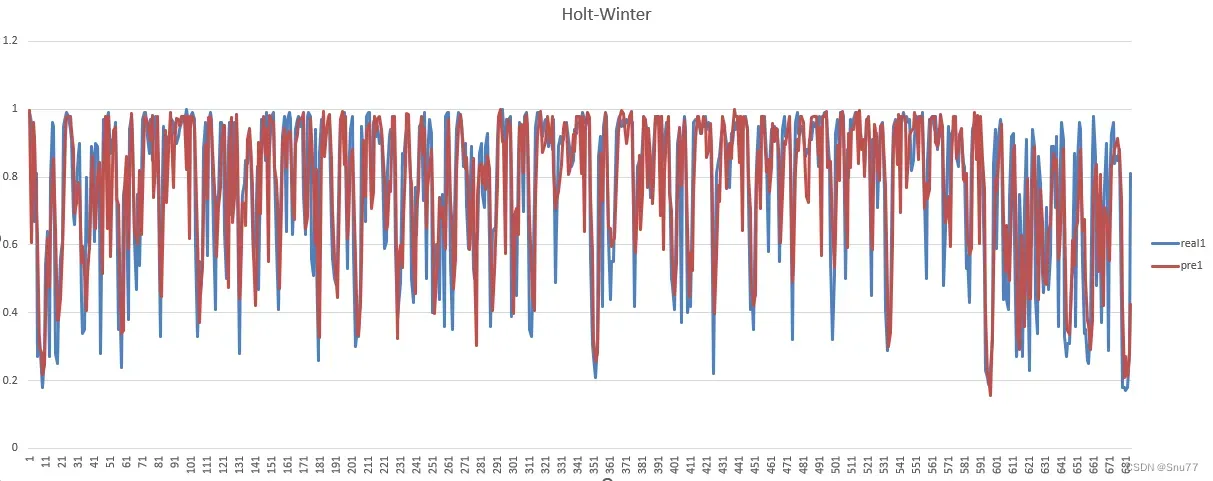
话不多说上来先上预测精度分析图,其中MAE的误差大概在0.11,以下数据均是预测未知数据，而不是训练数据的预测图。
开始之前我们先来简单了解一下Holt-Winters模型
Holt-Winters模型，也称为三重指数平滑模型，是一种经典的时间序列预测模型，用于处理具有趋势和季节性的时间序列数据。
Holt-Winters模型基于指数平滑法，通过对历史数据进行加权平均来预测未来的值。它使用三个指数平滑系数来估计未来的趋势、季节性和平稳项，从而可以对未来的值进行预测。
Holt-Winters模型的三个指数平滑系数分别为：α、β和γ。其中，α表示对当前观测值的加权系数，β表示对趋势的加权系数，γ表示对季节性的加权系数。这些系数可以通过利用K-折交叉验证最小化平均绝对误差或平均平方误差来确定。
Holt-Winters模型大致可以分为三种类型：加法模型、乘法模型和季节性模型。加法模型适用于季节性变化的幅度相对稳定的情况，乘法模型适用于季节性变化的幅度随着趋势的变化而变化的情况，季节性模型则适用于季节性变化的周期相对稳定的情况。
本文主要选择一种模型来进行实现(季节性模型)同时利用K-折交叉验证法来确定其中三个平滑系数α、β和γ以验证最好的系数,从而达到最高的预测精度极限。
下面来接介绍一下什么是K-折交叉验证
K-折交叉验证（K-fold cross-validation）是一种常用的模型评估方法，用于评估机器学习模型的性能和泛化能力。它将原始数据集分成K个子集，称为“折叠”（fold），其中K-1个子集用于训练模型，1个子集用于测试模型。这个过程重复K次，每个子集都会轮流作为测试集，最终得到K个模型的性能评估结果，这些结果可以平均或加权平均得到模型的最终性能评估结果。
K-折交叉验证的优点是可以有效地利用数据集，减少因数据划分不合理而引入的偏差，提高模型的泛化能力。同时，K-折交叉验证可以避免过拟合和欠拟合等问题，提高模型的稳定性和可靠性。
数据格式
在正式开始之前需要先了解一下，holt-winter模型是单元变量预测模型,所以其只接受单个时间变量的时间序列预测,所以其数据只需要一列即可,就是你需要预测的数据我们这里拿官方的数据ETTh1来进行举例
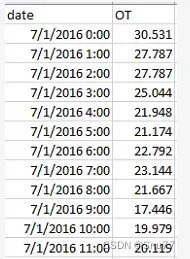
数据是这种格式即可,当然你也可以只有OT一列数据也可以,但是你要确保你的数据要符合时间序列,因为你的顺序不能够打乱，因为我们需要时间date这一列主要是为了确保数据是有序的，当然如果你确定你的数据是有序的你也可以只读取进来一列数据即可！！！
运行代码
Holt-Winters模型主体
大家可以新建一个py文件将以下所有代码复制进去加上你的数据即可运行出结果！！
import pandas as pd
import numpy as np
from scipy.optimize import minimize # 优化函数
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import TimeSeriesSplit
class HoltWinters:
def __init__(self, series, slen, alpha, beta, gamma, n_preds, scaling_factor=1.96):
self.series = series
self.slen = slen
self.alpha = alpha
self.beta = beta
self.gamma = gamma
self.n_preds = n_preds
self.scaling_factor = scaling_factor
def initial_trend(self):
"""
初始化趋势，使用第一个原始数据周期内的数据
依据现有的数据，除非输入的原始数据发生变化，否则为常数
:return: 初始化的趋势
"""
sum = 0.0
for i in range(self.slen):
sum += float(self.series[i + self.slen] - self.series[i]) / self.slen
return sum / self.slen
def initial_seasonal_components(self):
"""
初始化季节性参数
:return: 季节性对于当周期平均值的平均变化值
"""
seasonals = {}
season_averages = []
# 现有数据的周期个数
n_seasons = int(len(self.series) / self.slen)
# let's calculate season averages
# 最后一个周期会有稍微的影响，但影响不大
# 每个周期平均值，从第一个周期开始，共有n个周期的数据
for j in range(n_seasons):
season_averages.append(sum(self.series[self.slen * j:self.slen * j + self.slen]) / float(self.slen))
# let's calculate initial values
# 周期中第i天的季节性增长（对比周期内的平均值）
# 数据个数为一个周期的长度，index为一个周期内的第几个值，从0开始
# 与原始数据相关，并不是一个固定值
for i in range(self.slen):
sum_of_vals_over_avg = 0.0
for j in range(n_seasons):
sum_of_vals_over_avg += self.series[self.slen * j + i] - season_averages[j]
seasonals[i] = sum_of_vals_over_avg / n_seasons
return seasonals
def triple_exponential_smoothing(self):
"""
三次指数平滑
:return:
"""
# 预测结果
self.result = []
# 平滑值
self.Smooth = []
# 季节性
self.Season = []
# 趋势性
self.Trend = []
# 预测标准差
self.PredictedDeviation = []
self.UpperBond = []
self.LowerBond = []
# 对于当周期的平均值，每一时刻的平均变化值，为初始值
seasonals = self.initial_seasonal_components()
for i in range(len(self.series) + self.n_preds):
if i == 0: # components initialization
smooth = self.series[0]
trend = self.initial_trend()
self.result.append(self.series[0])
self.Smooth.append(smooth)
self.Trend.append(trend)
self.Season.append(seasonals[i % self.slen])
self.PredictedDeviation.append(0)
self.UpperBond.append(self.result[0] +
self.scaling_factor *
self.PredictedDeviation[0])
self.LowerBond.append(self.result[0] -
self.scaling_factor *
self.PredictedDeviation[0])
continue
if i >= len(self.series): # predicting
m = i - len(self.series) + 1
self.result.append((smooth + m * trend) + seasonals[i % self.slen])
# self.result.append(max(0,min(1, (smooth + m * trend) + seasonals[i % self.slen])))
# when predicting we increase uncertainty on each step
# 每一步增加预测的波动性
self.PredictedDeviation.append(self.PredictedDeviation[-1] * 1.01)
else:
val = self.series[i]
last_smooth, smooth = smooth, self.alpha * (val - seasonals[i % self.slen]) + (1 - self.alpha) * (
smooth + trend)
trend = self.beta * (smooth - last_smooth) + (1 - self.beta) * trend
seasonals[i % self.slen] = self.gamma * (val - smooth) + (1 - self.gamma) * seasonals[i % self.slen]
self.result.append(smooth + trend + seasonals[i % self.slen])
# self.result.append(max(0,min(1, smooth + trend + seasonals[i % self.slen])))
# Deviation is calculated according to Brutlag algorithm.
self.PredictedDeviation.append(self.gamma * np.abs(self.series[i] - self.result[i])
+ (1 - self.gamma) * self.PredictedDeviation[-1])
self.UpperBond.append(self.result[-1] +
self.scaling_factor *
self.PredictedDeviation[-1])
self.LowerBond.append(self.result[-1] -
self.scaling_factor *
self.PredictedDeviation[-1])
self.Smooth.append(smooth)
self.Trend.append(trend)
self.Season.append(seasonals[i % self.slen])
def timeseriesCVscore(params, series, loss_function=mean_squared_error, slen=7):
"""
Returns error on CV
params - vector of parameters for optimization
series - dataset with timeseries
slen - season length for Holt-Winters model
"""
# errors array
errors = []
values = series.values
alpha, beta, gamma = params
# set the number of folds for cross-validation
# tscv = TimeSeriesSplit(n_splits=50, test_size=4)
tscv = TimeSeriesSplit(n_splits=5, test_size=4)
# iterating over folds, train model on each, forecast and calculate error
for train, test in tscv.split(values):
model = HoltWinters(series=values[train], slen=slen,
alpha=alpha, beta=beta, gamma=gamma, n_preds=len(test))
model.triple_exponential_smoothing()
predictions = model.result[-len(test):]
actual = values[test]
error = loss_function(predictions, actual)
errors.append(error)
return np.mean(np.array(errors)) # 返回了一个损失函数的平均值以上的部分就是Holt-Winters的程序内部，其中有一些个人阅读时候的个人理解,大家可以在阅读时候进行一个参考,
程序入口
下面的代码就是程序的入口,我们复制粘贴到文件的最后面即可，下面我将介绍其中每一行的具体含义！！
if __name__ == '__main__':
data = pd.read_csv('')
# initializing model parameters alpha, beta and gamma
cycle = '在这里输入你数据的周期'
pre_len = '这里输入你要预测未来多久的数据'
# Minimizing the loss function
opt = minimize(timeseriesCVscore, x0=[0, 0, 0],
args=(data, mean_squared_error,),
method="TNC", bounds=((0, 1), (0, 1), (0, 1))
)
# Take optimal values...
alpha, beta, gamma = opt.x
model = HoltWinters(data, slen=cycle,
alpha=alpha,
beta=beta,
gamma=gamma,
n_preds=pre_len, scaling_factor=2)
model.triple_exponential_smoothing()
print(model.result)
参数讲解
首先data = pd.read_csv(”)这一行很好理解就是读取你的数据,首先要求你的数据需要是csv格式的文件,然后读取来的数据要满足第二节所述的数据格式（如果你的文件是其他格式你也可以更换类似于read_excel()即可）
data = pd.read_csv('')当我们将数据读取进来之后,我们可以对数据进行一个按照时间排序的操作(如果你的数据只有目标值列而没有时间列则忽略掉本段代码) 这一段代码如果你们没有也可以运行如果需要排序则可以自己复制粘贴到对应位置即可
data.sort_values(by=['date'], inplace=True)之后的两行，这两行是一个是你数据拥有的周期性,因为holt-winter模型主要的参数还是你数据的一个周期来预测未来某一时段的数据,所有你要知道你数据所拥有的周期性,可以通过数据建模的方式或者根据你的经验来分析(如果大家不会可以评论区留言我可以给大家出用powerbi,matplotlib，excel来建模从而分析数据的教程)
cycle = '在这里输入你数据的周期'
pre_len = '这里输入你要预测未来多久的数据'这一段代码如果大家了解深度学习就可以理解为模型训练的一个过程,其中
timeseriesCVscore是一个K-折交叉验证的方法来求出损失值最小的方法,
x0就是Holt-Winters模型的三个参数α、β和γ我们初始时将其设置为0
args=(data,mean_squared_error) 其中data就是你们读取进来的数据, mean-squared_error就是一个军方损失函数,就是用前面的K-折交叉验证来求这一损失函数的最小值
method=’TNC’就是模型训练的从而收敛的方法,其有很多选项如下大家可以多做实验从而得到一个最好损失结果,
– ‘Nelder-Mead’ :ref:`(see here) <optimize.minimize-neldermead>`
– ‘Powell’ :ref:`(see here) <optimize.minimize-powell>`
– ‘CG’ :ref:`(see here) <optimize.minimize-cg>`
– ‘BFGS’ :ref:`(see here) <optimize.minimize-bfgs>`
– ‘Newton-CG’ :ref:`(see here) <optimize.minimize-newtoncg>`
– ‘L-BFGS-B’ :ref:`(see here) <optimize.minimize-lbfgsb>`
– ‘TNC’ :ref:`(see here) <optimize.minimize-tnc>`
– ‘COBYLA’ :ref:`(see here) <optimize.minimize-cobyla>`
– ‘SLSQP’ :ref:`(see here) <optimize.minimize-slsqp>`
– ‘trust-constr’:ref:`(see here) <optimize.minimize-trustconstr>`
– ‘dogleg’ :ref:`(see here) <optimize.minimize-dogleg>`
– ‘trust-ncg’ :ref:`(see here) <optimize.minimize-trustncg>`
– ‘trust-exact’ :ref:`(see here) <optimize.minimize-trustexact>`
– ‘trust-krylov’ :ref:`(see here) <optimize.minimize-trustkrylov>`
每一个方法都不一样,不同的数据也可能适合不同的方法大家可以多尝试尝试,
bounds就是限制α、β和γ的范围其通常都是位于0-1之间的一个数字,我们限制其一下不要让其超出范围！
opt = minimize(timeseriesCVscore, x0=[0, 0, 0],
args=(data, mean_squared_error,),
method="TNC", bounds=((0, 1), (0, 1), (0, 1))
)之后的代码就是将我们训练好的三个参数α、β和γ取出来
alpha, beta, gamma = opt.x下面的代码就是正式到我们预测的部分了,其中的大部分参数我们都已经讲过了,除了其中的scaling_factor大家可以将其理解为一个平滑的参数，之后就是我们对输出结果作了一个三指数的平滑操作可以让数据更加平滑从而提高精度！！！
model = HoltWinters(data, slen=cycle,
alpha=alpha,
beta=beta,
gamma=gamma,
n_preds=pre_len, scaling_factor=2)
model.triple_exponential_smoothing()最后我们打印一下结果即可
print(model.result)
开始训练
将上述准备工作全部做完以后我们就可以运行我们的程序开始训练了！
运行你们保存代码的文件,控制台就会输出训练过程
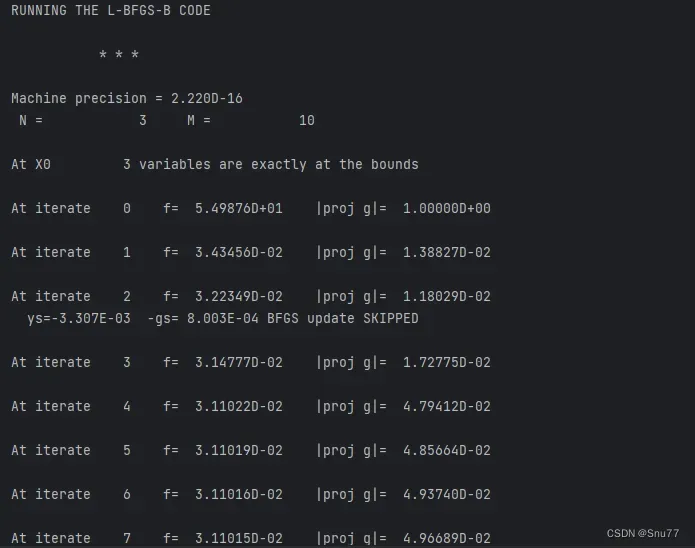我这里选用的method是L-BFGS-B这个对于我的数据而言我能拿到更高的精度,其控制台输出如上图所示,直到其最终收敛！
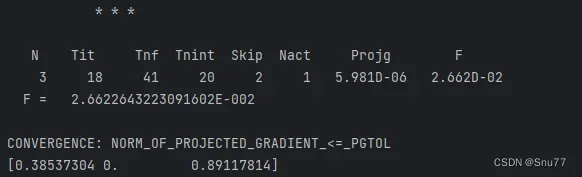
可以看到控制台收敛以后打印出了 α、β和γ三个参数,其中α=0.38537304、β=0和γ=0.89117814
α表示对当前观测值的加权系数，β表示对趋势的加权系数，γ表示对季节性的加权系数。
预测结果
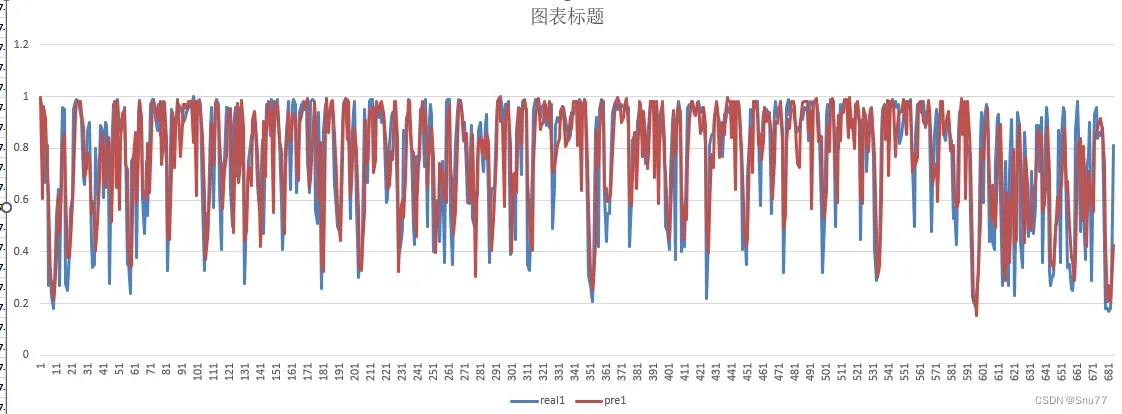
我将所有的结果输出下来并进行了保存到本地的csv文件中并用excel画出了如图可以看出预测值和真实值之间的误差还是有一定误差的！
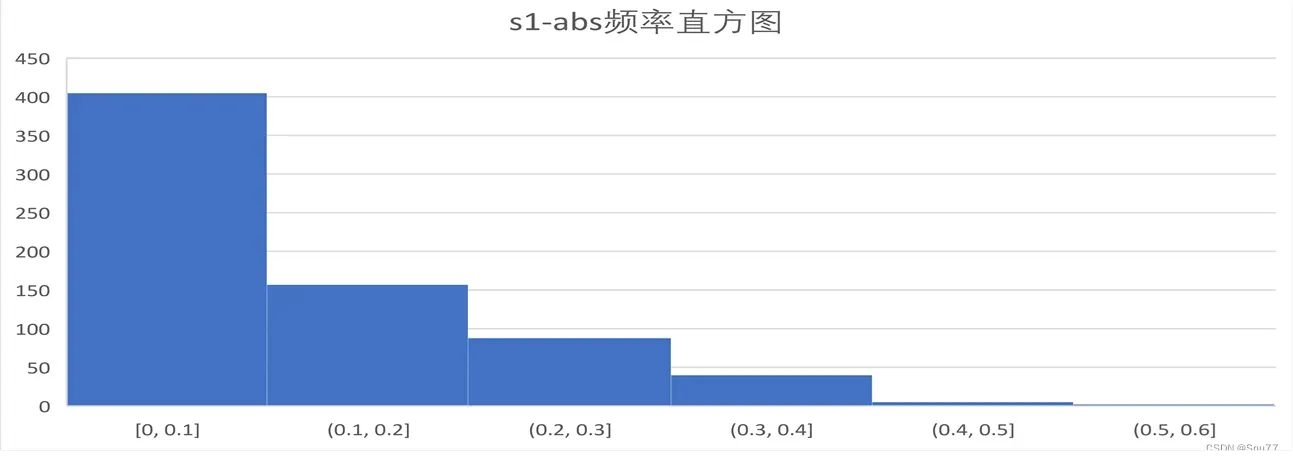
这个图可以看出我们的误差MAE大部分都集中在0-0.1之间预测效果还是可以的！
到此Holt-Winters模型的使用就讲解完了！！！！！希望大家都能运行出一个好的结果！
其它时间序列预测模型讲解
后期我会讲一些最新的预测模型包括transform, Informer，TPA-LSTM,ARIMA,XGBOOST,Holt-winter，移动平均法等等一系列关于时间序列预测的模型,包括深度学习和机器学习方向的模型我都会讲,你可以根据需求选取适合你自己的模型进行预测，如果有需要可以+个关注，包括本次模型我自己的代码和数据大家有需要我也会放出百度网盘下载链接！！
—————————————————–MTS-Mixers————————————————————
【全网首发】(MTS-Mixers)(Python)(Pytorch)最新由华为发布的时间序列预测模型实战案例(一)(包括代码讲解)实现企业级预测精度包括官方代码BUG修复Transform模型
——————————————————–LSTM—————————————————————–
时间序列预测模型实战案例(三)(LSTM)(Python)(深度学习)时间序列预测(包括运行代码以及代码讲解)
如果大家有不懂的也可以评论区留言一些报错什么的大家可以讨论讨论看到我也会给大家解答如何解决！
文章出处登录后可见！
