【大道至简】机器学习算法之隐马尔科夫模型(Hidden Markov Model, HMM)详解（2）—计算问题：前向算法和后向算法原理详解公式推导及Python实现

☕️ 本文系列文章汇总：
（1）HMM开篇：基本概念和几个要素
（2）HMM计算问题：前后向算法
（3）HMM学习问题：Baum-Welch算法
（4） HMM预测问题：维特比算法
☕️ 本文来自专栏：大道至简之机器学习系列专栏
❤️各位小伙伴们关注我的大道至简之机器学习系列专栏，一起学习各大机器学习算法
❤️还有更多精彩文章（NLP、热词挖掘、经验分享、技术实战等），持续更新中……欢迎关注我，个人主页：https://blog.csdn.net/qq_36583400，记得点赞+收藏哦！
📢个人GitHub地址：https://github.com/fujingnan

先总结一波：

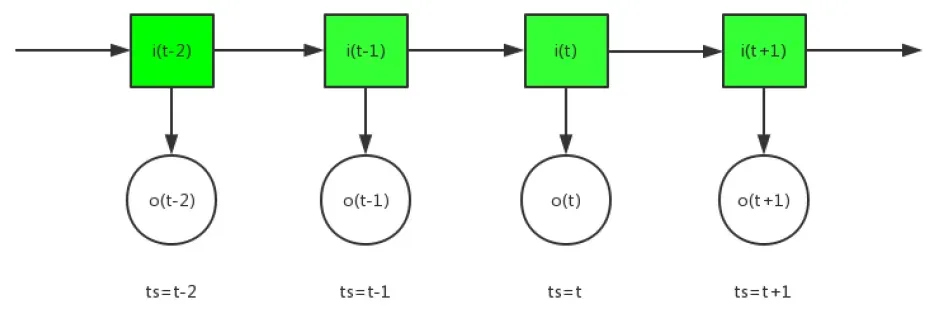
通俗点讲，前向算法是从源头向终点出发，每走一步都要利用先前的经验来判断这一步怎么走；后向算法是从终点开始向本源出发，每走一步都通过已有的现象来判断其更深层的原因。

数学点讲，前向算法：给定隐马尔科夫模型λ，定义到时刻t为止的这部分观测序列为o1,o2,…,ot且时刻t的状态值为 $i_{t}=q_{i}$ 的概率为前向概率，记作：

$\alpha _{t}(i)=P(o_{1},o_{2},...,o_{t},i_{t}=q_{i}|\lambda)$

算法流程：

输入：隐马尔科夫模型λ以及观测序列O；
输出：观测序列的概率P(O|λ)
（1）计算初值：
$\alpha_{1}(i)=\pi_{i}b_{i}(o_{1}), i=1,2,...,N$ (1)
（2）递推向后计算每一步的概率，对t=1,2,…,T-1：
$\alpha_{t+1}(i)=\left [ \sum_{j=1}^{N}\alpha_{t}(j)a_{ji} \right ]b_{i}(o_{t+1}),i=1,2,...,N$ (2)
（3）最终概率：
$P(O|\lambda)=\sum_{i=1}^{N}\alpha_{T}(i)$ (3)

后向算法：给定隐马尔科夫模型λ，定义在时刻t状态为 $q_{i}$ 的条件下，从t+1到T的这部分观测序列为 $o_{t+1},o_{t+2},...,o_{T}$ 的概率称为后向概率，记作：

$\beta_{t}(i)=P(o_{t+1},o_{t+2},...,o_{T}|i_{t}=q_{i},\lambda)$

算法流程：

输入：隐马尔科夫模型λ，观测序列O
输出：观测序列概率P(O|λ)
（1）计算初值。
$\beta_{T}(i)=1, \quad i=1,2,...,N \qquad (1)$
（2）对t=T-1，T-2，…，1时刻往前计算：
$\beta_{t}(i)=\sum_{j=1}^{N}a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j), \quad i=1,2,...,N \qquad (2)$
（3）计算最终结果：
$P(O|\lambda)=\sum_{i=1}^{N}\pi_{i}b_{i}(o_{1})\beta_{1}(i) \qquad (3)$

上一篇文末我们提到了隐马尔科夫模型的三个基本问题：概率计算问题、学习问题、预测问题。那么本篇我们就来讲一下概率计算问题。

在讲概率计算问题之前，先来回顾一下隐马尔科夫模型的概念：

概念：隐马尔科夫模型描述了一个由隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成每一个观测从而产生观测随机序列的过程。换句话说，就是它是一个具有时间序列特点的模型，这个时间序列有三个显要特点：1）每一个时间点包含了一个隐藏值；2）当前时刻的隐藏值在下一时刻会以特定的概率发生转移，不同概率转移成不同的隐藏值，且转移后的隐藏值将“定居”在下一时刻，当前时刻的隐藏值保持不变；3）每一刻所包含的隐藏值会以特定的概率产生一个观测值，不同的隐藏值、不同的概率均会产生不同观测值。

其中，每个时间点（状态）用i表示，其包含的隐藏值（状态值）用q表示，所有时间点组成的序列称为状态序列，用I表示， $I=\{i_{1, }i_{2},...,i_{T}\}$ ，所有可能的隐藏值组成了状态集合，用Q表示， $Q=\{q_{1},q_{2},...,q_{N}\}$ ，每个时间点产生的观测事件（观测）用o表示，观测的结果（观测值）用v表示，时间序列下的观测事件称为观测序列，用O表示， $O=\{o_{1},o_{2},...,o_{T}\}$ ，所有可能的观测结果组成观测集合，用V表示， $V=\{v_{1},v_{2},...,v_{M}\}$ 。不同状态值相互转换的概率组成状态转移概率矩阵A，不同状态值产生不同观测值的概率组成观测概率矩阵B。

数学模型：λ=(π，A，B)，π是初始转移概率向量，A是状态转移概率矩阵，B是观测概率矩阵。

应用：

1. 如果已经有了一个隐马尔科夫模型λ后，可以计算该模型产生特定观测序列O的概率是多少；

2. 如果只有一个观测序列，那么可以通过计算估计出一个模型λ，且该模型参数的条件下能够产生你所观测到的结果的可能性最大；

3. 如果已经有了一个隐马尔科夫模型λ，并且得到了一个观测序列O，可以求出最有可能的对应的状态序列I。

上述第一个应用就是本章将要讲的概率计算问题。

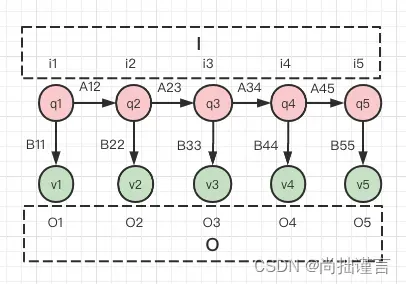
图1 隐马尔科夫模型示意图

一、何为概率计算

不要把问题想复杂了，概率计算问题就是我们常规意义上的条件概率的计算。那么在隐马尔科夫模型的应用1中，我们的已知条件是什么呢？显然是λ：π、A、B以及O。所以啊，我们要求的就是在λ已知的情况下，生成观测O的概率，即P(O|λ)。

但是需要注意的是，不管从哪个角度来分析，P(O|λ)都少不了隐变量I，即状态序列，再怎么说，λ也包含了A，而A就是和I有关系的，所以，上述概率需要把I加上并转化成边缘概率对I的积分形式，即：

$P(O|\lambda )=\sum_{I}P(O,I|\lambda)=\sum_{I}P(O|I,\lambda)P(I|\lambda)$

如果这个式子的变换还没有反应过来，可以参考我写过的【大道至简】机器学习算法之EM算法(Expectation Maximization Algorithm)详解(附代码)—通俗理解EM算法。_尚拙谨言的博客-CSDN博客_em算法代码实现所以我们就来分别计算一下P(O|I, λ)和 P(I|λ)就可以了，注意这里头假设状态序列I的长度为T，而我们的状态一共有N种可能。

来吧，上述两者的计算其实也是常规计算，对于条件概率P(I|λ)来说，因为我们已经知道了A，而A表示各个状态之间转移的概率，所以啊，要想知道某个整个I的概率，那就是每个小i的概率连乘，通俗点就是“这个概率发生的条件下那个概率发生的概率，这个概率发生且那个概率发生的条件下那那个概率发生的概率……”。所以：

$P(I|\lambda)=\pi_{i_{1}}a_{i_{1}i_{2}}a_{i_{2}i_{3}}...a_{i_{T-1}i_{T}}$

而我们又已知了B，它表示每个隐状态产生每种观测结果的概率，所以在给定某个I和B的条件下，我们已知的观测序列O出现的概率为每个观测值v出现的概率的连乘：

$P(O|I,\lambda)=b_{i_{1}}(o_{1})b_{i_{2}}(o_{2})...b_{i_{T}}(o_{T})$

这个式子的理解和 P(I|λ) 的理解是一样的。

所以，我们最终的概率为：

$\begin{aligned} P(O|\lambda) &= \sum_{I}P(O|I,\lambda)P(I|\lambda)\\ &= \sum_{I}\pi_{i_{1}}a_{i_{1}i_{2}}a_{i_{2}i_{3}}...a_{i_{T-1}i_{T}}b_{i_{1}}(o_{1})b_{i_{2}}(o_{2})...b_{i_{T}}(o_{T}) \end{align}$

我们来分析一下时间复杂度啊，现在我们的状态序列I长度为T，每个状态i都有N种可能取值，所以I一共可以取N^T种可能，即需要计算N^T这么多次，对于每一种可能，由于我们的观测序列是已知的，所以每一种可能的状态序列中的每一个状态，都需要计算一次观测概率，T个状态就需要计算T次观测概率（1+1+…+1=T），综合就是每种可能的状态序列需要计算T次，所以N^T种状态序列就需要计算T*N^T次，也就是上述计算方式的时间复杂度为 $O(TN^T)$ 。这么高的时间复杂度，当T很大时，上述方法我们啧啧啧、、、看看就好。

上述方法也叫直接计算法或者叫暴力求解法，学过数据结构算法的小伙伴，应该都知道，很多暴力求解法都有更优化的方法来实现，那就是—动态规划。所以隐马尔科夫模型概率计算问题也不例外，我们当然有更好的方式来求解啦，这就是我们下面将要介绍的两种方法：前向计算法和后向计算法。

二、前向算法

前向和后向算法都是解决HMM概率计算问题的有力武器，其基本思想类似动态规划。先来介绍一下什么是前向算法。

简单来说，就是当前时刻的概率只和前一时刻的概率有关，而前一时刻的概率，又由再前前时刻的概率计算而来，以此类推，每一次计算当前时刻概率的时候，都只用到前一时刻的概率即可，因为它已经包含了前面所有时刻的概率计算的信息了，这样一来，计算的复杂度将大大降低。

正儿八经的定义前向概率：给定隐马尔科夫模型λ，定义到时刻t为止的这部分观测序列为o1,o2,…,ot且时刻t的状态值为 $i_{t}=q_{i}$ 的概率为前向概率，记作：

$\alpha _{t}(i)=P(o_{1},o_{2},...,o_{t},i_{t}=q_{i}|\lambda)$

先抛出算法流程，后面会用课本上的例子逐一讲解：

输入：隐马尔科夫模型λ以及观测序列O；
输出：观测序列的概率P(O|λ)
（1）计算初值：
$\alpha_{1}(i)=\pi_{i}b_{i}(o_{1}), i=1,2,...,N$ (1)
（2）递推向后计算每一步的概率，对t=1,2,…,T-1：
$\alpha_{t+1}(i)=\left [ \sum_{j=1}^{N}\alpha_{t}(j)a_{ji} \right ]b_{i}(o_{t+1}),i=1,2,...,N$ (2)
（3）最终概率：
$P(O|\lambda)=\sum_{i=1}^{N}\alpha_{T}(i)$ (3)

用人话解释一下：上面公式（1），意思是在初始时刻的时候，当状态转移概率π分别为i=1,2,…,N种概率的情况下，分别计算生成的观测值b为o1的概率，即为初始前向概率；公式（2）中，递推意指利用当前步已知的概率来计算下一时刻的前向概率，在时刻为t的时候，当状态转移概率a为第i种概率时，计算当前时刻由状态j从第一种情况到第N种情况向第i种状态转移的概率之和，为下一时刻的状态出现的概率 $P(i_{t+1}=q_{i_{t+1}}|i_{t}=q_{i_{t}})$ ，再乘以b，即在该状态出现概率的条件下生成观测 $o_{t+1}$ 的概率，称为t+1时刻的前向概率，这里有几个i，就要分别算出几个α，令t=t+1，重复上述过程，最终将所有的α相加，得到P(O|λ)。

如果还是云里雾里没关系，我们下面会用课本上一个很好地例子细细说明。现在先来看下前向算法的时间复杂度：感观上理解，对于一个状态序列来讲，假如序列长度为T，一共有N种可能的状态，那么对于相邻的两个状态，当前时刻的状态有N种可能，转移到下一时刻的状态也有N种可能，所以两个状态间的转移就有N^2种可能，因为我们这边是递推的过程，每次计算下一时刻的状态只需要用到当前状态即可，所以一共需要计算T次，每次都有N^2种可能，T次就有T*N^2种可能，故时间复杂度为 $O(TN^2)$ 。每次计算都可以直接用前一次计算的结果而避免了重复计算，这可比直接计算的暴力求解法快太多了。

现在我们一起来分析一下课本上的例子，例子来源于《统计学习方法》李航第二版 P200页：

在例子中，我们已经有了模型λ的各个参数A、B和π了，且我们已经观测到了结果，那就是第一次取到的是红球、第二次是白球，第三次是红球，观测序列为 $(o_{1},o_{2},o_{1})$ 对于各个已知量的理解，如果不清楚的，请一定回看上一篇中第三节。

解答：

1. 计算第一个观测值出现的概率

$\alpha_{1}(i)=\pi_{i}b_{i}(o_{1}), i=1,2,...,N$

分析：如果要让第一个观测值为红球，那么由初始概率向量可以看出有以下几种可能：

1）红球是从盒子1中取出的。当前盒子为盒子1的概率为0.2，从盒子1中取到红球的概率为 $b_{1}(o_{1})$ ，所以“当前盒子为1，且从盒子1中取得红球的概率”为：

$\alpha_{1}(1)=\pi_{1}b_{1}(o_{1})=0.2\times 0.5=0.1$

2）红球是从盒子2中取出的。当前盒子为盒子2的概率为0.4，从盒子2中取到红球的概率为 $b_{2}(o_{1})$ ，所以“当前盒子为2，且从盒子2中取得红球的概率”为：

$\alpha_{1}(2)=\pi_{2}b_{2}(o_{1})=0.4\times 0.4=0.16$

3）红球是从盒子3中取出的。当前盒子为盒子3的概率为0.4，从盒子3中取到红球的概率为 $b_{3}(o_{1})$ ，所以“当前盒子为3，且从盒子3中取得红球的概率”为：

$\alpha_{1}(3)=\pi_{3}b_{3}(o_{1})=0.4\times 0.7=0.28$

2. 计算第二个观测值出现的概率

$\alpha_{t+1}(i)=\left [ \sum_{j=1}^{N}\alpha_{t}(j)a_{ji} \right ]b_{i}(o_{t+1}),i=1,2,...,N$

向后递推计算。

分析：当第二个观测值为白球，那么它有以下几种可能：

1）【如果当前盒子为1】

a. 上一时刻状态为盒子1且从盒子1中取到的是红球，且当前时刻状态为盒子1，且从当前的盒子1中取得白球。上一时刻状态为盒子1且从盒子1中取到的是红球的概率为 $\alpha_{1}(1)$ ，上一时刻为盒子1转移到当前时刻为盒子1的概率为0.5，从盒子1中取得白球的概率为0.5，所以“上一时刻状态为盒子1且从盒子1中取到的是红球，且当前时刻状态为盒子1，且从当前的盒子1中取得白球”的概率为：

$\alpha_{2}(1\Rightarrow 1)=\alpha_{1}(1)a_{11}b_{1}(o_{2})=0.1\times0.5\times0.5=0.025$

b. 上一时刻状态为盒子2且从盒子2中取到的是红球，且当前时刻状态为盒子1，且从当前的盒子1中取得白球。上一时刻状态为盒子2且从盒子2中取到的是红球的概率为 $\alpha_{1}(2)$ ，上一时刻为盒子2转移到当前时刻为盒子1的概率为0.3，从盒子1中取得白球的概率为0.5，所以“上一时刻状态为盒子2且从盒子2中取到的是红球，且当前时刻状态为盒子1，且从当前的盒子1中取得白球”的概率为：

$\alpha_{2}(2\Rightarrow 1)=\alpha_{1}(2)a_{21}b_{1}(o_{2})=0.16\times0.3\times0.5=0.024$

c. 上一时刻状态为盒子3且从盒子3中取到的是红球，且当前时刻状态为盒子1，且从当前的盒子1中取得白球。上一时刻状态为盒子3且从盒子3中取到的是红球的概率为 $\alpha_{1}(3)$ ，上一时刻为盒子3转移到当前时刻为盒子1的概率为0.2，从盒子1中取得白球的概率为0.5，所以“上一时刻状态为盒子3且从盒子3中取到的是红球，且当前时刻状态为盒子1，且从当前的盒子1中取得白球”的概率为：

$\alpha_{2}(3\Rightarrow 1)=\alpha_{1}(3)a_{31}b_{1}(o_{2})=0.28\times0.2\times0.5=0.028$

所以，当前盒子为1，且观测值为白球的概率为以上可能性相加：

$\alpha_{2}(1)=0.025+0.024+0.028=0.077$

2）【如果当前盒子为2】

a. 上一时刻状态为盒子1且从盒子1中取到的是红球，且当前时刻状态为盒子2，且从当前的盒子2中取得白球。上一时刻状态为盒子1且从盒子1中取到的是红球的概率为 $\alpha_{1}(1)$ ，上一时刻为盒子1转移到当前时刻为盒子2的概率为0.2，从盒子2中取得白球的概率为0.6，所以“上一时刻状态为盒子1且从盒子1中取到的是红球，且当前时刻状态为盒子2，且从当前的盒子2中取得白球”的概率为：

$\alpha_{2}(1\Rightarrow 2)=\alpha_{1}(1)a_{12}b_{2}(o_{2})=0.1\times0.2\times0.6=0.012$

b. 上一时刻状态为盒子2且从盒子2中取到的是红球，且当前时刻状态为盒子2，且从当前的盒子2中取得白球。上一时刻状态为盒子2且从盒子2中取到的是红球的概率为 $\alpha_{1}(2)$ ，上一时刻为盒子2转移到当前时刻为盒子2的概率为0.5，从盒子2中取得白球的概率为0.6，所以“上一时刻状态为盒子2且从盒子2中取到的是红球，且当前时刻状态为盒子2，且从当前的盒子2中取得白球”的概率为：

$\alpha_{2}(2\Rightarrow 2)=\alpha_{1}(2)a_{22}b_{2}(o_{2})=0.16\times0.5\times0.6=0.048$

c. 上一时刻状态为盒子3且从盒子3中取到的是红球，且当前时刻状态为盒子2，且从当前的盒子2中取得白球。上一时刻状态为盒子3且从盒子3中取到的是红球的概率为 $\alpha_{1}(3)$ ，上一时刻为盒子3转移到当前时刻为盒子2的概率为0.3，从盒子2中取得白球的概率为0.6，所以“上一时刻状态为盒子3且从盒子3中取到的是红球，且当前时刻状态为盒子2，且从当前的盒子2中取得白球”的概率为：

$\alpha_{2}(3\Rightarrow 2)=\alpha_{1}(3)a_{32}b_{2}(o_{2})=0.28\times0.3\times0.6=0.0504$

所以，当前盒子为2，且观测值为白球的概率为以上可能性相加：

$\alpha_{2}(2)=0.012+0.048+0.0504=0.1104$

3）【如果当前盒子为3】

a. 上一时刻状态为盒子1且从盒子1中取到的是红球，且当前时刻状态为盒子3，且从当前的盒子3中取得白球。上一时刻状态为盒子1且从盒子1中取到的是红球的概率为 $\alpha_{1}(1)$ ，上一时刻为盒子1转移到当前时刻为盒子3的概率为0.3，从盒子3中取得白球的概率为0.3，所以“上一时刻状态为盒子1且从盒子1中取到的是红球，且当前时刻状态为盒子3，且从当前的盒子3中取得白球”的概率为：

$\alpha_{2}(1\Rightarrow 3)=\alpha_{1}(1)a_{13}b_{3}(o_{2})=0.1\times0.3\times0.3=0.009$

b. 上一时刻状态为盒子2且从盒子2中取到的是红球，且当前时刻状态为盒子3，且从当前的盒子3中取得白球。上一时刻状态为盒子2且从盒子2中取到的是红球的概率为 $\alpha_{1}(2)$ ，上一时刻为盒子2转移到当前时刻为盒子3的概率为0.2，从盒子3中取得白球的概率为0.3，所以“上一时刻状态为盒子2且从盒子2中取到的是红球，且当前时刻状态为盒子3，且从当前的盒子3中取得白球”的概率为：

$\alpha_{2}(2\Rightarrow 3)=\alpha_{1}(2)a_{23}b_{3}(o_{2})=0.16\times0.2\times0.3=0.0096$

c. 上一时刻状态为盒子3且从盒子3中取到的是红球，且当前时刻状态为盒子3，且从当前的盒子3中取得白球。上一时刻状态为盒子3且从盒子3中取到的是红球的概率为 $\alpha_{1}(3)$ ，上一时刻为盒子3转移到当前时刻为盒子3的概率为0.5，从盒子3中取得白球的概率为0.3，所以“上一时刻状态为盒子3且从盒子3中取到的是红球，且当前时刻状态为盒子3，且从当前的盒子3中取得白球”的概率为：

$\alpha_{2}(3\Rightarrow 3)=\alpha_{1}(3)a_{33}b_{3}(o_{2})=0.28\times0.5\times0.3=0.042$

所以，当前盒子为3，且观测值为白球的概率为以上可能性相加：

$\alpha_{2}(3)=0.009+0.0096+0.042=0.0606$

3. 计算第三个观测值出现的概率

按照第二个观测值一模一样的分析逻辑，我们很容易可以得到第三个观测值的概率，这里不再赘述，直接写结果：

a. 如果第三个观测值是从盒子1取得的红球，其概率为：

$\alpha_{3}(1)=\sum_{i=1}^{3}\left [ \alpha_{2}(i)a_{i1} \right ]b_{1}(o_{3})=0.04187$

b. 如果第三个观测值是从盒子2取得的红球，其概率为：

$\alpha_{3}(2)=\sum_{i=1}^{3}\left [ \alpha_{2}(i)a_{i2} \right ]b_{2}(o_{3})=0.03551$

c. 如果第三个观测值是从盒子3取得的红球，其概率为：

$\alpha_{3}(3)=\sum_{i=1}^{3}\left [ \alpha_{2}(i)a_{i3} \right ]b_{3}(o_{3})=0.05284$

所以，第三个观测值为红球的概率为以上3种可能性相加：

$P(O|\lambda)=\sum_{i=1}^{3}\alpha_{3}(i)=0.13022$

P(O|λ) 也是本例的最终结果，为什么呢？因为按照动态规划的思想，当前概率已经包含了前面所有情况的概率计算结果，也就是假如我们要知道第二个观测值为白球的所有可能性，那么就是 $\sum_{i=1}^{3}\alpha_{2}(i)=0.077+0.1104+0.0606=0.248$ 。

至此，我们的前向计算方法就讲解完毕。虽然推导过程看上去有点绕，比较复杂，但是如果用代码实现，只需要写好动态规划的公式即可，一切就交给计算机处理就好了。相信大家对前向计算的方法已经有了一个较清晰的认识了。

既然有前向算法，那就存在后向算法，下面我们再介绍一下后向算法。

三、后向算法

后向算法是这么定义的：给定隐马尔科夫模型λ，定义在时刻t状态为 $q_{i}$ 的条件下，从t+1到T的这部分观测序列为 $o_{t+1},o_{t+2},...,o_{T}$ 的概率称为后向概率，记作：

$\beta_{t}(i)=P(o_{t+1},o_{t+2},...,o_{T}|i_{t}=q_{i},\lambda)$

对于后向算法的理解，从定义出发非常重要。我看网上包括很多教学视频，对这部分内容的讲解几乎是一笔带过，基本上都是说：~~和前向算法类似，只不过这边是反过来计算而已，这里不再多说了，大家自己看书~~。我觉得这么说是很不负责任的，因为对于大多数数学天赋没那么好的人真的仔细理解后向算法，还是需要花点时间的，如果没有人指点，可能真的就需要费很大劲（我就是）。为了让大伙不再走太多弯路，我接下来尽最大可能把自己已经搞明白的知识给大家分享。

输入：隐马尔科夫模型λ，观测序列O
输出：观测序列概率P(O|λ)
（1）计算初值。
$\beta_{T}(i)=1, \quad i=1,2,...,N \qquad (1)$
（2）对t=T-1，T-2，…，1时刻往前计算：
$\beta_{t}(i)=\sum_{j=1}^{N}a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j), \quad i=1,2,...,N \qquad (2)$
（3）计算最终结果：
$P(O|\lambda)=\sum_{i=1}^{N}\pi_{i}b_{i}(o_{1})\beta_{1}(i) \qquad (3)$

其实后向算法我个人认为最不好理解的就是 $\beta_{T}(i)=1$ 这个东西，我尝试着从多个角度去深刻理解它，都失败了，怎么都说不通，最后我回归到定义，终于搞明白了，所以各位，定义，定义是非常重要的！顺便插一嘴，我们平时的生活中，会遇到各种各样复杂的问题，如果我们从复杂的问题本身来思考，往往会越思考越复杂，因为问题本来就是基于复杂的表象呈现的，你在一个复杂的问题上思考，肯定是解决不了的，就好比要求你在一个残次的设备上做出惊世绝品，不敢说不可能，只能说很难。这个时候，我们往往要回归复杂问题的本源来思考，因为大多数复杂问题无非就是一个个简单的小问题组成的，如果你能学会将大问题不断深入递推的分解成小问题，然后按照关联性排序和分层，逐个分析，找到最根本的问题突破它，往往能助你找到大问题的解决方法。所以，本源思维非常之重要。

好了，看下这个T时刻的β为啥是1吧。定义上说， $\beta_{t}(i)$ 表示已知时刻t状态为 $q_{i}$ 的条件下，从t+1到T的这部分观测序列为 $o_{t+1},o_{t+2},...,o_{T}$ 的概率，那么在T时刻呢？把T带到定义里一目了然： $\beta_{T}(i)$ 表示已知时刻T状态为 $q_{i}$ 的条件下，从T到T的这部分观测序列为 $o_{T}$ 的概率。那么由于T时刻的状态已知，不管T时刻的状态是哪个，从T时刻到T时刻本身的状态概率显然是1，换句通俗点的话说：你是你自己的概率显然是1，而T时刻本身的观测值又是已知的，T时刻的状态已知，它产生的观测又已知，那么T时刻的已知状态产生已知观测的概率是个必然事件，为1。一切都是在T时刻自身上算，啥啥都已知，概率为1，不管几个1相乘，仍为1，所以T时刻的β值必然是1。

解释了初始β为1的原因后，我们就可进行下一步的计算了。还是以前向算法中的那个例子来举例。

已知模型的参数如下：

（1）现在第三个观测值是红球的情况有以下三种：

1）第三个观测值为红球来自盒子1的概率为： $\beta_{3}(1)=1$ ；

2）第三个观测值为红球来自盒子2 的概率为： $\beta_{3}(2)=1$ ；

3）第三个观测值为红球来自盒子3的概率为： $\beta_{3}(3)=1$ ；

（2）那么第二个观测值为白球有以下几种可能：

1）第二个观测值为白球来自盒子1且第三个观测值为红球来自盒子1、第二个观测值为白球来自盒子1且第三个观测值为红球来自盒子2、第二个观测值为白球来自盒子1且第三个观测值为红球来自盒子3。所以当第二个状态为盒子1的条件下，第三时刻观测序列为“红球”的后向概率为上述三种情况相加：

$\begin{align*} \beta_{2}(1)&=a_{11}b_{3}(1)\beta_{3}(1)+a_{12}b_{3}(2)\beta_{3}(2)+a_{13}b_{3}(3)\beta_{3}(3)\\&=0.5\times0.5\times1+0.2\times0.4\times1+0.3\times0.7\times1\\&=0.54 \end{aligned}$

2）第二个观测值为白球来自盒子2且第三个观测值为红球来自盒子1、第二个观测值为白球来自盒子2且第三个观测值为红球来自盒子2、第二个观测值为白球来自盒子2且第三个观测值为红球来自盒子3。所以当第二个状态为盒子2的条件下，第三时刻观测序列为“红球”的后向概率为上述三种情况相加：

$\begin{aligned} \beta_{2}(2)&=a_{21}b_{3}(1)\beta_{3}(1)+a_{22}b_{3}(2)\beta_{3}(2)+a_{23}b_{3}(3)\beta_{3}(3)\\&=0.3\times0.5\times1+0.5\times0.4\times1+0.2\times0.7\times1\\&=0.49 \end{}$

3）第二个观测值为白球来自盒子3且第三个观测值为红球来自盒子1、第二个观测值为白球来自盒子3且第三个观测值为红球来自盒子2、第二个观测值为白球来自盒子3且第三个观测值为红球来自盒子3。所以当第二个状态为盒子3的条件下，第三时刻观测序列为“红球”的后向概率为上述三种情况相加：

$\begin{aligned} \beta_{2}(3)&=a_{31}b_{3}(1)\beta_{3}(1)+a_{32}b_{3}(2)\beta_{3}(2)+a_{33}b_{3}(3)\beta_{3}(3)\\&=0.2\times0.5\times1+0.3\times0.4\times1+0.5\times0.7\times1\\&=0.57 \end{}$

（3）第一个观测值为红球有以下几种可能：

1）第一个观测值为红球来自盒子1且第二个观测值为白球来自盒子1、第一个观测值为红球来自盒子1且第二个观测值为白球来自盒子2、第一个观测值为红球来自盒子1且第二个观测值为白球来自盒子3。所以当第一个状态为盒子1的条件下，从第二时刻到第三时刻观测序列为“白球，红球”的后向概率为上述三种情况相加：

$\begin{aligned} \beta_{1}(1)&=a_{11}b_{2}(1)\beta_{2}(1)+a_{12}b_{2}(2)\beta_{2}(2)+a_{13}b_{2}(3)\beta_{2}(3)\\&=0.5\times0.5\times0.54+0.2\times0.6\times0.49+0.3\times0.3\times0.57\\&=0.2451 \end{}$

2）第一个观测值为红球来自盒子2且第二个观测值为白球来自盒子1、第一个观测值为红球来自盒子2且第二个观测值为白球来自盒子2、第一个观测值为红球来自盒子2且第二个观测值为白球来自盒子3。所以当第一个状态为盒子2的条件下，从第二时刻到第三时刻观测序列为“白球，红球”的后向概率为上述三种情况相加：

$\begin{aligned} \beta_{1}(2)&=a_{21}b_{2}(1)\beta_{2}(1)+a_{22}b_{2}(2)\beta_{2}(2)+a_{23}b_{2}(3)\beta_{2}(3)\\&=0.3\times0.5\times0.54+0.5\times0.6\times0.49+0.2\times0.3\times0.57\\&=0.2622 \end{}$

3）第一个观测值为红球来自盒子3且第二个观测值为白球来自盒子1、第一个观测值为红球来自盒子3且第二个观测值为白球来自盒子2、第一个观测值为红球来自盒子3且第二个观测值为白球来自盒子3。所以当第一个状态为盒子3的条件下，从第二时刻到第三时刻观测序列为“白球，红球”的后向概率为上述三种情况相加：

$\begin{aligned} \beta_{1}(3)&=a_{31}b_{2}(1)\beta_{2}(1)+a_{32}b_{2}(2)\beta_{2}(2)+a_{33}b_{2}(3)\beta_{2}(3)\\&=0.2\times0.5\times0.54+0.3\times0.6\times0.49+0.5\times0.3\times0.57\\&=0.2277 \end{}$

你以为结束了？注意看后向算法的定义：定义 $\beta_{t}(i)$ 是从t+1到T时刻的概率，所以截止到上述我们求得的 $\beta_{1}(i)$ 只是初始状态为π的条件下，从第二个状态到第三个状态这部分的观测序列为(白球，红球)时的概率，但是很显然我们要求的是从第一时刻到第三时刻状态下观测序列为（红球，白球，红球）的概率，也就是t=1到t=3这部分观测序列为（红球，白球，红球）的概率，由定义可知，要求这部分的概率，就需要知道t-1时刻的状态值，幸运的是，我们知道！就是我们的π，所以本例中第一时刻作如下分析：

1）当初始状态为盒子1时，从第一时刻到第三时刻观测序列为“红球，白球，红球”的后向概率为：

$\begin{aligned} \beta_{1}'(1)&=\pi_{1}b_{1}(1)\beta_{1}(1)\\&= 0.2\times0.5\times0.2451\\&=0.02451 \end{}$

2）当初始状态为盒子2时，从第一时刻到第三时刻观测序列为“红球，白球，红球”的后向概率为：

$\begin{aligned} \beta_{1}'(2)&=\pi_{2}b_{2}(1)\beta_{1}(2)\\&= 0.4\times0.4\times0.2622\\&=0.041952 \end{}$

3）当初始状态为盒子3时，从第一时刻到第三时刻观测序列为“红球，白球，红球”的后向概率为：

$\begin{aligned} \beta_{1}'(3)&=\pi_{3}b_{3}(1)\beta_{1}(3)\\&= 0.4\times0.7\times0.2277\\&=0.063756 \end{}$

综上所述，从时刻1到时刻3观测序列为“红球，白球，红球”的概率为：

$\begin{aligned} P(O|\lambda)&=\sum_{i=1}^{N}\pi_{i}b_{i}(o_{1})\beta_{1}(i)\\&=\beta'_{1}(1)+\beta'_{1}(2)+\beta'_{1}(3) \\&=0.02451+0.041952+0.063756\\&=0.130218\end{}$

至此后向算法的讲解完毕。通过以上例子可以看出，利用前向算法和后向算法求解P(O|λ)的结果几乎是一样的，说明这两种算法对于计算隐马尔科夫模型概率计算问题都是有效的，当然也说明咱们这一波繁杂的计算是对的(捏一把冷汗==)。

四、代码实现

代码地址：ml_algorithm/隐马尔科夫模型 at master · fujingnan/ml_algorithm · GitHub

（1）版本一：

import numpy as np

class FB:
    def __init__(self, pi, A, B, V):
        """
        初始化模型参数
        :param pi: 初始状态概率向量
        :param A: 已学习得到的状态转移概率矩阵，这里直接引用课本中的例子10.2
        :param B: 已学习得到的概率矩阵，这里直接引用课本中的例子10.2
        :param V: 已知的观测集合，同样使用例子中的值
        """
        self.pi = pi
        self.A = A
        self.B = B
        self.V = V

    def cal_prob(self, O, opt):
        if opt == 'f':
            metrix = self.forward(O)
            # 计算P(O|λ) 公式10.17
            return sum(metrix[-1])
        elif opt == 'b':
            # 计算P(O|λ) 公式10.21
            metrix = self.backward(O)
            return sum(metrix[-1])


    def forward(self, O):
        """
        前向算法
        :param O: 已知的观测序列
        :return: P(O|λ)
        """
        row, col = len(O), self.A.shape[0]
        alpha_t_plus_1 = np.zeros((row, col), dtype=float)
        for t, o in enumerate(O):
            if t == 0:
                # 初值α 公式10.15
                for i, p in enumerate(self.pi):
                    obj_index = self.V.index(o)
                    alpha_t_plus_1[t][i] = p * self.B[i][obj_index]
            else:
                # 递推 公式10.16
                for i in range(self.A.shape[0]):
                    alpha_ji = 0.
                    # 公式10.16里中括号的内容
                    for j, a in enumerate(alpha_t_plus_1[t-1]):
                        alpha_ji += (a * self.A[j][i])
                    obj_index = self.V.index(o)
                    # 公式10.16
                    alpha_t_plus_1[t][i] = alpha_ji * self.B[i][obj_index]

        return alpha_t_plus_1

    def backward(self, O):
        """
        后向算法
        :param O: 已知的观测序列
        :return: P(O|λ)
        """
        row, col = len(O), self.A.shape[0]
        betaT = np.zeros((row+1, col), dtype=float)

        for t, o in enumerate(O[::-1]):
            if t == 0:
                # 初值β 公式10.19
                betaT[t][:] = [1] * self.A.shape[0]
                continue
            else:
                # 反向递推 公式10.20
                for i in range(self.A.shape[0]):
                    beta_t = 0.
                    obj_index = self.V.index(O[t - 1])
                    for j, b in enumerate(betaT[t-1]):
                        beta_t += (self.A[i][j] * self.B[j][obj_index] * b)
                    betaT[t][i] = beta_t
        betaT[-1][:] = [self.pi[i] * self.B[i][self.V.index(O[0])] * betaT[-2][i] for i in range(self.A.shape[0])]
        return betaT

if __name__ == '__main__':
    from time import time
    # 课本例子10.2
    pi = [0.2, 0.4, 0.4]
    a = np.array([
        [0.5, 0.2, 0.3],
        [0.3, 0.5, 0.2],
        [0.2, 0.3, 0.5]
    ])
    b = np.array([
        [0.5, 0.5],
        [0.4, 0.6],
        [0.7, 0.3]
    ])
    O = ['红', '白', '红']
    f = FB(pi=pi, A=a, B=b, V=['红', '白'])
    # start = time()
    resf = f.forward(O)
    resb = f.backward(O)
    # print(time()-start)
    print('α：{}\n前向算法的概率计算结果：{}'.format(resf, f.cal_prob(O, opt='f')))
    print('β：{}\n后向算法的概率计算结果：{}：'.format(resb, f.cal_prob(O, opt='b')))

（2）版本二（优化1）：

import numpy as np

class FB:
    def __init__(self, pi, A, B, V):
        """
        初始化模型参数
        :param pi: 初始状态概率向量
        :param A: 已学习得到的状态转移概率矩阵，这里直接引用课本中的例子10.2
        :param B: 已学习得到的概率矩阵，这里直接引用课本中的例子10.2
        :param V: 已知的观测集合，同样使用例子中的值
        """
        self.pi = np.array(pi)
        self.A = np.array(A)
        self.B = np.array(B)
        self.V = V

    def cal_prob(self, O, opt):
        if opt == 'f':
            metrix = self.forward(O)
            # 计算P(O|λ) 公式10.17
            return sum(metrix[-1])
        elif opt == 'b':
            # 计算P(O|λ) 公式10.21
            metrix = self.backward(O)
            return sum(metrix[-1])


    def forward(self, O):
        """
        前向算法
        :param O: 已知的观测序列
        :return: P(O|λ)
        """
        row, col = len(O), self.A.shape[0]
        alpha_t_plus_1 = np.zeros((row, col), dtype=float)
        obj_index = self.V.index(O[0])
        # 初值α 公式10.15
        alpha_t_plus_1[0][:] = self.pi * self.B[:].T[obj_index]
        for t, o in enumerate(O[1:]):
            t += 1
            # 递推 公式10.16
            obj_index = self.V.index(o)
            for i in range(self.A.shape[0]):
                # 公式10.16
                alpha_ji = alpha_t_plus_1[t-1][:] @ self.A[:].T[i]
                alpha_t_plus_1[t][i] = alpha_ji * self.B[i][obj_index]

        return alpha_t_plus_1

    def backward(self, O):
        """
        后向算法
        :param O: 已知的观测序列
        :return: P(O|λ)
        """
        row, col = len(O), self.A.shape[0]
        betaT = np.zeros((row+1, col), dtype=float)
        # 初值β 公式10.19
        betaT[0][:] = [1] * self.A.shape[0]
        for t, o in enumerate(O[::-1][1:]):
            t += 1
            # 反向递推 公式10.20
            obj_index = self.V.index(O[t-1])
            for i in range(self.A.shape[0]):
                beta_t = self.A[i][:] * self.B[:].T[obj_index] @ betaT[t-1][:].T
                betaT[t][i] = beta_t
        betaT[-1][:] = [self.pi[i] * self.B[i][self.V.index(O[0])] * betaT[-2][i] for i in range(self.A.shape[0])]
        return betaT

if __name__ == '__main__':
    # 课本例子10.2
    from time import time
    pi = [0.2, 0.4, 0.4]
    a = np.array([
        [0.5, 0.2, 0.3],
        [0.3, 0.5, 0.2],
        [0.2, 0.3, 0.5]
    ])
    b = np.array([
        [0.5, 0.5],
        [0.4, 0.6],
        [0.7, 0.3]
    ])
    O = ['红', '白', '红']
    f = FB(pi=pi, A=a, B=b, V=['红', '白'])
    start = time()
    resf = f.forward(O)
    resb = f.backward(O)
    print(time() - start)
    print(f.cal_prob(O, opt='f'))

（3）版本三（优化2）：

import numpy as np

class FB:
    def __init__(self, pi, A, B, V):
        """
        初始化模型参数
        :param pi: 初始状态概率向量
        :param A: 已学习得到的状态转移概率矩阵，这里直接引用课本中的例子10.2
        :param B: 已学习得到的概率矩阵，这里直接引用课本中的例子10.2
        :param V: 已知的观测集合，同样使用例子中的值
        """
        self.pi = np.array(pi)
        self.A = np.array(A)
        self.B = np.array(B)
        self.V = V

    def cal_prob(self, O, opt):
        if opt == 'f':
            metrix = self.forward(O)
            # 计算P(O|λ) 公式10.17
            return sum(metrix[-1])
        elif opt == 'b':
            # 计算P(O|λ) 公式10.21
            metrix = self.backward(O)
            return sum(metrix[-1])


    def forward(self, O):
        """
        前向算法
        :param O: 已知的观测序列
        :return: P(O|λ)
        """
        row, col = len(O), self.A.shape[0]
        alpha_t_plus_1 = np.zeros((row, col), dtype=float)
        obj_index = self.V.index(O[0])
        # 初值α 公式10.15
        alpha_t_plus_1[0][:] = self.pi * self.B[:].T[obj_index]
        for t, o in enumerate(O[1:]):
            t += 1
            # 递推 公式10.16
            obj_index = self.V.index(o)
            alpha_ji = alpha_t_plus_1[t - 1][:].T @ self.A
            alpha_t_plus_1[t][:] = alpha_ji * self.B[:].T[obj_index]

        return alpha_t_plus_1

    def backward(self, O):
        """
        后向算法
        :param O: 已知的观测序列
        :return: P(O|λ)
        """
        row, col = len(O), self.A.shape[0]
        betaT = np.zeros((row+1, col), dtype=float)
        # 初值β 公式10.19
        betaT[0][:] = [1] * self.A.shape[0]
        for t, o in enumerate(O[::-1][1:]):
            t += 1
            # 反向递推 公式10.20
            obj_index = self.V.index(O[t-1])
            beta_t = self.A * self.B[:].T[obj_index] @ betaT[t-1][:].T
            betaT[t][:] = beta_t
        betaT[-1][:] = [self.pi[i] * self.B[i][self.V.index(O[0])] * betaT[-2][i] for i in range(self.A.shape[0])]
        return betaT

if __name__ == '__main__':
    from time import time
    # 课本例子10.2
    pi = [0.2, 0.4, 0.4]
    a = np.array([
        [0.5, 0.2, 0.3],
        [0.3, 0.5, 0.2],
        [0.2, 0.3, 0.5]
    ])
    b = np.array([
        [0.5, 0.5],
        [0.4, 0.6],
        [0.7, 0.3]
    ])
    O = ['红', '白', '红']
    f = FB(pi=pi, A=a, B=b, V=['红', '白'])
    start = time()
    resf = f.forward(O)
    resb = f.backward(O)
    print(time() - start)
    print(f.cal_prob(O, opt='b'))

五、总结

通过以上分析，我们深入理解了概率计算问题中重要的两种算法：前向算法和后向算法。前向算法主要是利用上一时刻的计算结果来推算出下一时刻的结果，即已知当前情况，那么下一步的情况是啥。后向算法主要是已知当前时刻的状态以及下一时刻起到终止时刻的结果来推算从当前时刻到终止时刻的结果的概率。通俗点讲，前向算法是从源头向终点出发，每走一步都要利用先前的经验来判断这一步怎么走；后向算法是从终点开始向本源出发，每走一步都通过已有的现象来判断其更深层的原因。

本人不擅长画图，所以喜欢图文并茂的同学，这里推荐一篇博客大家可以参考着看：用摸鱼学来解释隐马尔可夫模型(HMM) – 知乎

不管是哪种算法，我们都要掌握，因为它们的思想实在是太重要了！！！

现在我们解决了已知模型λ和观测结果，求观测结果发生的概率计算问题，那么问题来了，如果我只是知道观测结果而还没有得到一个模型咋整？这就是下一篇我们要介绍的隐马尔科夫模型另一个经典问题：学习问题。
小伙伴们，点赞+关注，学习不迷路哦~

文章出处登录后可见！

已经登录？立即刷新