🤵‍♂️ 个人主页：@艾派森的个人主页

✍🏻作者简介：Python学习者
🐋 希望大家多多支持，我们一起进步！😄
如果文章对你有帮助的话，
欢迎评论 💬点赞👍🏻 收藏 📂加关注+

目录

推断统计与参数检验

假设检验 

两配对样本t检验

两配对样本t检验的应用

 【SPSS】专栏正在不断更新中，感兴趣的小伙伴可以点个订阅支持一下

推断统计与参数检验

推断统计

• 推断统计方法是根据样本数据推断总体特征的方法
• 推断统计包括参数估计 (点估计和区间估计)和假设检验两大类 

参数检验 VS 非参数检验

• 参数检验（参数假设检验）

总体分布已知 （如总体为正态分布）的情况下,根据样本数据对总体分布的统计参数(如均值、方差等)进行推断

• 非参数检验（非参数假设检验）

总体分布未知的情况下,根据样本数据对总体的分布形式或数字特征进行推断 

假设检验 

假设检验的基本思想

1 首先，对总体参数值提出假设

2 然后，利用样本告知的信息去验证先前提出的假设是否成立

• 如果样本数据不能够充分证明和支持假设,则应拒绝假设
• 如果样本数据能够充分证明和支持假设,则不能推翻假设 

小概率原理：

• 发生概率很小的随机事件在某一次特定的实验中是几乎不可能发生的
• 小概率原理是假设检验所依据的原理 

假设检验的基本步骤

1.提出原假设(记为H0 )和备择假设(记为H1 ) 通常，将希望推翻的假设放在原假设上

2.选择检验统计量：检验统计量服从或近似服从某种已知的理论分布

3.计算概率P值：在认为原假设成立的条件下,根据样本数据和检验统计量计算 概率P值,该概率值间接地给出了样本值(或更极端值)在原假设成 立条件下发生的概率，即：P(拒绝H0|H0为真) 

4.给定显著性水平α,并作出统计决策：显著性水平α是在原假设H0正确的前提下却拒绝原假设的概率，即“弃真”概率，一般设定为 0.05或0.01 若概率P值小于等于α，拒绝原假设；否则，不能拒绝原假设 

两配对样本t检验

 两配对样本t检验介绍

• 配对样本的含义：可以是个案在“前” “后”两种状态下某属性的两种不同特征
• 配对样本的特征
  • 两个样本的样本量相同
  • 两个样本观测值的先后顺序是一 一对应的，不能随意更改
• 目的：利用来自两个总体的配对样本，推断两个总体的均值是否存在显著差异

例如：为研究某减肥茶是否有显著的减肥效果，需要对抽取的肥胖人群喝茶前与喝茶后的体重进行分析。

两配对样本t检验的基本步骤

        两配对样本t检验是通过单样本t检验来实现的，即最终转化成对 差值样本总体均值是否与0有显著差异做检验。

1 提出原假设 H0 :μ1 -μ2=0

2 选择检验统计量

3 计算检验统计量的观测值和概率P值

4 给定显著性水平α，并作出决策

两配对样本t检验的应用

【案例】 为研究某种减肥茶是否具有明显的减肥效果，某机构对35名肥胖志愿者进行了减肥跟踪调研。首先将其喝减肥茶以前的体重记录下来，三个月后再依次将这35名志愿者喝茶后的体重记录下来。通过这两组样本数据的对比分析，推断减肥茶是否具有明显的减肥作用。 

操作步骤：

①选择菜单【分析】—-> 【比较均值】—-> 【配对样本T检验】

②选择配对检验变量到【配对变量(V)】框中

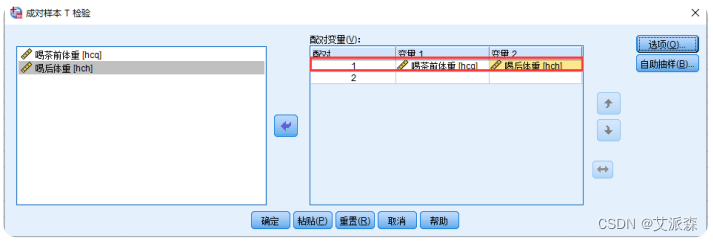
③分析结果如下： 

        结论：由第一个表可以看出，喝茶前与喝茶后样本的平均值有较大差异，这种差距是由偶然的还是系统性的，还需要进一步检验。

        第二个表描述了喝茶前后的线性相关性，说明喝茶前与喝茶后体重的线性相关程度较弱。

        第三个表中t检验统计量观测值对应的双侧概率P值接近0，小于显著性水平α，应该拒绝原假设，即认为减肥前后体重差的总体平均值与0有显著不同，意味着喝茶前与喝茶后的体重平均值存在显著差异，可以认为该减肥茶具有显著的减肥效果。