【Pytorch深度学习实战】（10）生成对抗网络（GAN）

 🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎

📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃

🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝​

📣系列专栏 – 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

目录

 🖍foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟👋

生成对抗网络 GAN 的基本原理

说到GAN第一篇要看的paper当然是Ian Goodfellow大牛的Generative Adversarial Networks（arxiv：https://arxiv.org/abs/1406.2661），这篇paper算是这个领域的开山之作。

GAN的基本原理其实非常简单，这里以生成图片为例进行说明。假设我们有两个网络，G（Generator）和D（Discriminator）。正如它的名字所暗示的那样，它们的功能分别是：

• G是一个生成图片的网络，它接收一个随机的噪声z，通过这个噪声生成图片，记做G(z)。
• D是一个判别网络，判别一张图片是不是“真实的”。它的输入参数是x，x代表一张图片，输出D（x）代表x为真实图片的概率，如果为1，就代表100%是真实的图片，而输出为0，就代表不可能是真实的图片。

在训练过程中，生成网络G的目标就是尽量生成真实的图片去欺骗判别网络D。而D的目标就是尽量把G生成的图片和真实的图片分别开来。这样，G和D构成了一个动态的“博弈过程”。

最后博弈的结果是什么？在最理想的状态下，G可以生成足以“以假乱真”的图片G(z)。对于D来说，它难以判定G生成的图片究竟是不是真实的，因此D(G(z)) = 0.5。

这样我们的目的就达成了：我们得到了一个生成式的模型G，它可以用来生成图片。

以上只是大致说了一下GAN的核心原理，如何用数学语言描述呢？这里直接摘录论文里的公式：

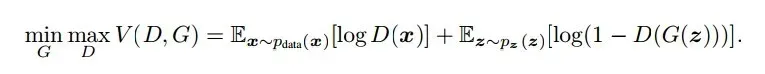
简单分析一下这个公式：

• 整个式子由两项构成。x表示真实图片，z表示输入G网络的噪声，而G(z)表示G网络生成的图片。
• D(x)表示D网络判断真实图片是否真实的概率（因为x就是真实的，所以对于D来说，这个值越接近1越好）。而D(G(z))是D网络判断G生成的图片的是否真实的概率。
• G的目的：上面提到过，D(G(z))是D网络判断G生成的图片是否真实的概率，G应该希望自己生成的图片“越接近真实越好”。也就是说，G希望D(G(z))尽可能得大，这时V(D, G)会变小。因此我们看到式子的最前面的记号是min_G。
• D的目的：D的能力越强，D(x)应该越大，D(G(x))应该越小。这时V(D,G)会变大。因此式子对于D来说是求最大(max_D)

下面这幅图片很好地描述了这个过程：

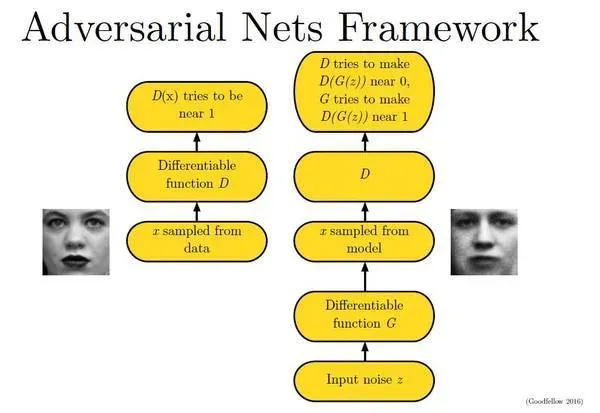
那么如何用随机梯度下降法训练D和G？论文中也给出了算法：

这里红框圈出的部分是我们要额外注意的。第一步我们训练D，D是希望V(G, D)越大越好，所以是加上梯度(ascending)。第二步训练G时，V(G, D)越小越好，所以是减去梯度(descending)。整个训练过程交替进行。

生成对抗网络Pytorch的实现

import os
import torch
import torchvision
import torch.nn as nn
from torchvision import transforms
from torchvision.utils import save_image


# 设备配置
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 超参数
latent_size = 64
hidden_size = 256
image_size = 784
num_epochs = 200
batch_size = 100
sample_dir = 'samples'

# 如果不存在则创建目录
if not os.path.exists(sample_dir):
    os.makedirs(sample_dir)

# 图像处理
# transform = transforms.Compose([
#                 transforms.ToTensor(),
#                 transforms.Normalize(mean=(0.5, 0.5, 0.5),   # 3 for RGB channels
#                                      std=(0.5, 0.5, 0.5))])
transform = transforms.Compose([
                transforms.ToTensor(),
                transforms.Normalize(mean=[0.5],   # 1 for greyscale channels
                                     std=[0.5])])

# MNIST 数据集
mnist = torchvision.datasets.MNIST(root='../../data/',
                                   train=True,
                                   transform=transform,
                                   download=True)

# 数据加载器
data_loader = torch.utils.data.DataLoader(dataset=mnist,
                                          batch_size=batch_size, 
                                          shuffle=True)

# 鉴别器
D = nn.Sequential(
    nn.Linear(image_size, hidden_size),
    nn.LeakyReLU(0.2),
    nn.Linear(hidden_size, hidden_size),
    nn.LeakyReLU(0.2),
    nn.Linear(hidden_size, 1),
    nn.Sigmoid())

# 生成器
G = nn.Sequential(
    nn.Linear(latent_size, hidden_size),
    nn.ReLU(),
    nn.Linear(hidden_size, hidden_size),
    nn.ReLU(),
    nn.Linear(hidden_size, image_size),
    nn.Tanh())

# 设备设置
D = D.to(device)
G = G.to(device)

# 二元交叉熵损失和优化器
criterion = nn.BCELoss()
d_optimizer = torch.optim.Adam(D.parameters(), lr=0.0002)
g_optimizer = torch.optim.Adam(G.parameters(), lr=0.0002)

def denorm(x):
    out = (x + 1) / 2
    return out.clamp(0, 1)

def reset_grad():
    d_optimizer.zero_grad()
    g_optimizer.zero_grad()

# 开始训练
total_step = len(data_loader)
for epoch in range(num_epochs):
    for i, (images, _) in enumerate(data_loader):
        images = images.reshape(batch_size, -1).to(device)
        
        # 创建稍后用作 BCE 损失输入的标签
        real_labels = torch.ones(batch_size, 1).to(device)
        fake_labels = torch.zeros(batch_size, 1).to(device)

        # ================================================================== #
        #                               训练判别器                           #
        # ================================================================== #

        # 使用真实图像计算 BCE_Loss 其中 BCE_Loss(x, y): - y * log(D(x)) - (1-y) * log(1 - D(x))
        # 损失的第二项总是为零，因为 real_labels == 1
        outputs = D(images)
        d_loss_real = criterion(outputs, real_labels)
        real_score = outputs
        
        # 使用假图像计算 BCELoss
        # 损失的第一项总是为零，因为 fake_labels == 0
        z = torch.randn(batch_size, latent_size).to(device)
        fake_images = G(z)
        outputs = D(fake_images)
        d_loss_fake = criterion(outputs, fake_labels)
        fake_score = outputs
        
        # 反向传播和优化
        d_loss = d_loss_real + d_loss_fake
        reset_grad()
        d_loss.backward()
        d_optimizer.step()
        
        # ================================================================== #
        #                             训练生成器                             #
        # ================================================================== #

        # 用假图像计算损失
        z = torch.randn(batch_size, latent_size).to(device)
        fake_images = G(z)
        outputs = D(fake_images)
        
        # 我们训练 G 最大化 log(D(G(z)) 而不是最小化 log(1-D(G(z)))
        # 原因见第3节最后一段。 https://arxiv.org/pdf/1406.2661.pdf
        g_loss = criterion(outputs, real_labels)
        
        # 反向传播和优化
        reset_grad()
        g_loss.backward()
        g_optimizer.step()
        
        if (i+1) % 200 == 0:
            print('Epoch [{}/{}], Step [{}/{}], d_loss: {:.4f}, g_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}' 
                  .format(epoch, num_epochs, i+1, total_step, d_loss.item(), g_loss.item(), 
                          real_score.mean().item(), fake_score.mean().item()))
    
    # 保存真实图片
    if (epoch+1) == 1:
        images = images.reshape(images.size(0), 1, 28, 28)
        save_image(denorm(images), os.path.join(sample_dir, 'real_images.png'))
    
    # 保存采样图像
    fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)
    save_image(denorm(fake_images), os.path.join(sample_dir, 'fake_images-{}.png'.format(epoch+1)))

# 保存模型checkpoints 
torch.save(G.state_dict(), 'G.ckpt')
torch.save(D.state_dict(), 'D.ckpt')