本文重点在第三部分“词嵌入”及对Word2vec的介绍,前面的知识主要用于小白对词表示和一些定义、名称的理解,和对一些方法不足的思考。
一、词表示
1.1 词表示的定义
词表示是一种将自然语言中的词转换为机器可理解含义的过程
其中意思(meaning)的定义 (Webster Dictionary) • The thing one intends to convey especially by language • The logical extension of a word
1.2 词表示的目标
计算词与词的相似度 • WR(Star) ≃ WR(Sun) • WR(Motel) ≃ WR(Hotel)
推测词与词的关系 • WR(China) − WR(Beijing) ≃ WR(Japan) – WR(Tokyo) • WR(Man) ≃ WR(King) − WR(Queen) + WR(Woman) • WR(Swimming) ≃ WR(Walking) − WR(Walk) + WR(Swim)
如何表示词的意思,使得机器可以理解?
1.3 过去的一些词表示方法
1.3.1 使用相关词集合,如同义词或上位词来对一个词进行表示
例如:WordNet是一个包含同义词和上位词的词典
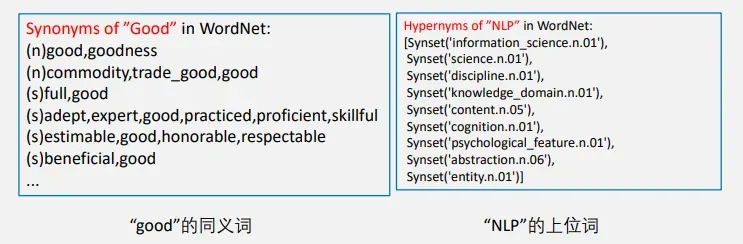
同义词/上位词表示的不足:
丢失语义上的细微差别:(“proficient”, “good”) 只在某些特定的上下文中为同义词
无法获得单词的新含义 :Apple (水果 → IT公司) ,Amazon (森林 → IT公司)
具有一定的主观性
数据稀疏
需要人工标注或更新
1.3.2 One-hot表示
将单词视为离散的符号,用单词的ID或one-hot表示,例如:
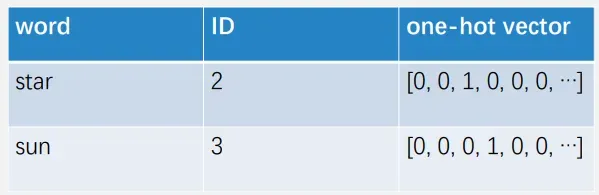
One-hot表示的不足
维度太高。
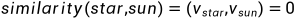 ,所有向量都互相正交,通过one-hot表示无法计算词与词的相似度
,所有向量都互相正交,通过one-hot表示无法计算词与词的相似度
1.3.3 上下文词表示 (Distributional Representation)
核心思想:一个词的意义应通过经常出现在其周围的词进行表示
基于统计学的自然语言处理中成功的想法之一
例如:使用上下文来表示单词stars
共现统计
词嵌入

接下来进行共现统计,基于计数的分布式词表示:
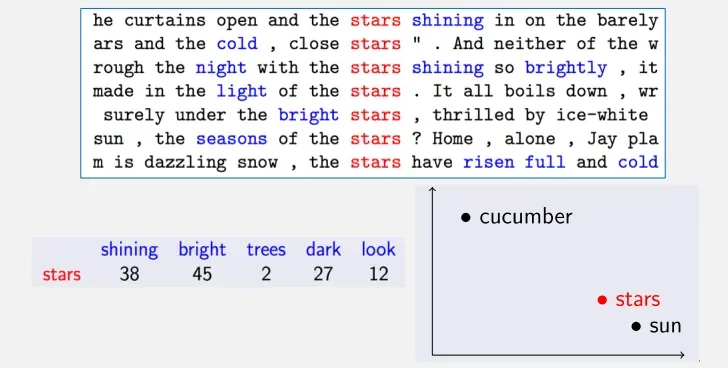
基于计数的分布式词表示其实也有一些细节上的不同:
Term-Term矩阵:矩阵中的数表示一个词出现在另一个词周围的次数
Term-Document矩阵:矩阵中的数表示一个词出现在某文档中的次数
Term-Term矩阵 (共现矩阵)
矩阵中的数表示一个词出现在另一个词周围的次数
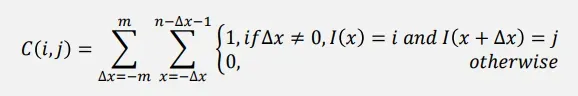
𝑛为句子的长度,𝑚为窗口长度
该共现矩阵同时获取句法和语义信息
窗口越小,词表示能包含越多句法信息 (𝑚 ∈ [1,3])
窗口越大,词表示能包含越多语义信息 (𝑚 ∈ [4,10])
例如:
语料
I like deep learning.
I like NLP.
I enjoy flying.
词表
I
Like
Deep
Learning
NLP
Enjoy
Flying
.
则 窗口长度为2时的Term-Term矩阵
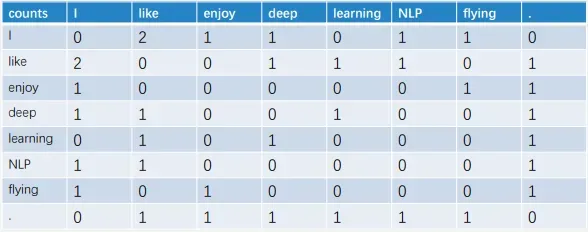
Term-Document矩阵
矩阵中的数表示一个词出现在文档中的次数(Document可以看作是一个最大的窗口,语义信息。)
例如:
语料
I like deep learning.
I like NLP.
I enjoy flying.
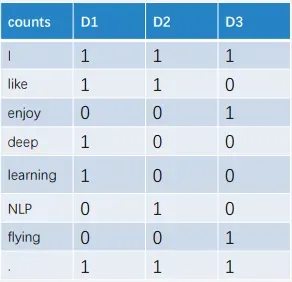
每个文档都由
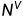 中的一个计 数向量 (一列) 表示
中的一个计 数向量 (一列) 表示
每个单词也由
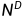 中的一个计 数向量 (一行) 表示
中的一个计 数向量 (一行) 表示
D表示语料中的文档数量,𝑉 表示词表大小
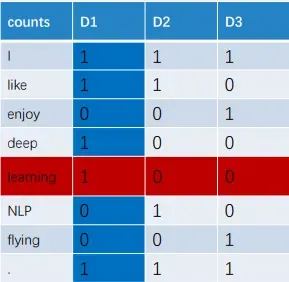
相似度计算
现有2个词向量𝑣和𝑤,可以通过点积计算他们的词间相似度
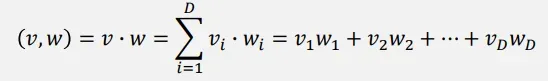
词向量长度反映该词的频度
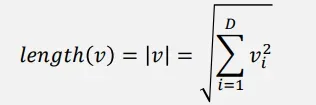
词向量长度越长表示该词出现得越频繁,点积值也更大。
可以基于向量长度对点积值进行标准化(不受长度影响),通常使用余弦相似度
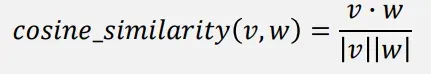
基于统计表示的不足
随词表增长规模变大→需要大量存储空间
低频词存在稀疏问题→导致后续语言处理模型表现不稳定
办法1:稠密向量
机器学习中的特征通常为低维稠密向量
稠密向量通常有更好的泛化能力
奇异值分解(SVD)介绍
M为𝑚 × 𝑛矩阵
M可以表示为𝑀 = 𝑈Σ𝑉*
U为𝑚 × 𝑘矩阵,行为原始行,但𝑘列分别为隐式空间中的一个维度,因此𝑘列向量 间两两正交
Σ为𝑘 × 𝑘奇异值对角矩阵,每一维度的值表示该维度的重要性
V*为𝑘 × 𝑛矩阵,列为原始列,但𝑘行分别与各奇异值相关
如果𝑘不够小,可以仅保留最大的𝑘个奇异值 (例如300),采用最小均方误 差逼近𝑀矩阵
SVD可以减小词向量的维度
SVD也可以应用于Term-Term矩阵 (共现矩阵),来得到稠密词向量
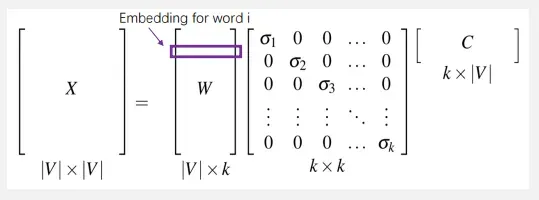
𝑋为Term-Term矩阵,𝑊中的每行为每个词w的𝑘维表示
办法2:词嵌入
分布式表示 (Distributed Representation)
通过对大规模文本语料的学习,为每一个词建立一个稠密向量表示
计算方法: word2vec
依旧是低维的稠密向量,思想来源于事物在人脑中的表示:分散在不同的神经元上,激活抑制的状态。单独的一个神经元激活或者一致的状态或许没什么用,但这些神经元组合在一起的激活抑制的状态所形成的低维的向量才有意义(组成某个词/句子意思等)
二、 分布式词表示
先来介绍一下语言模型
2.1 语言模型
关于词序列W的概率分布,即说出这句话/词的概率是多少
计算词序列的联合概率(覆盖率)
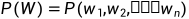
计算下一个词𝑤𝑛出现的条件概率
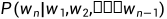
如何计算句子的概率?
假设: 下一个词的概率仅由它前面的词决定
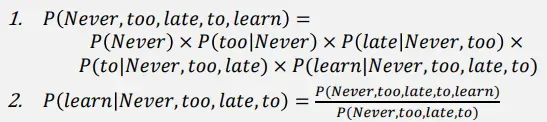
语言模型(下面这个公式的例子就是上面这个图片):
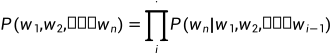
局限性:当句子长度很长时,句子概率的计算过程可能会很慢
办法:N-gram
限制前面的词的数量 (2 or 3)
用Back-off或smoothing方法处理新的单词组合
Markov假设
![]()
简化的语言模型

N-gram的不足
没有考虑1-2词之外的上下文信息
没有考虑词与词之间的相似度
The cat is walking in the bedroom
A dog was running in a room
N-gram没有考虑cat和dog,walking和running在语义和语法间的相似度
有鉴于此,我们需要神经语言模型
2.2 神经语言模型
神经语言模型是一种基于神经网络的语言模型,目的是学习词的分布式表示。
为每个词学习一个分布式向量
通过词的特征向量计算词序列的联合概率
学习优化词的分布式向量 (词嵌入矩阵E) 和模型其他参数 (映射矩阵W)
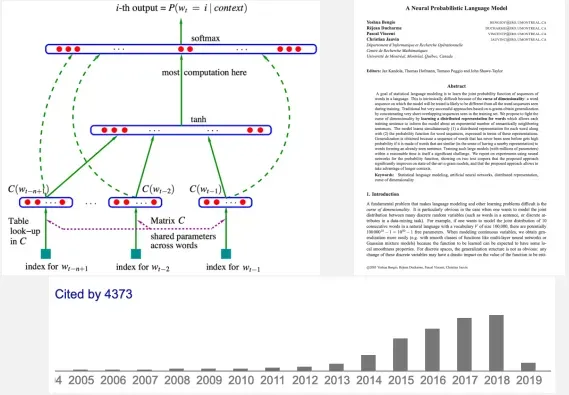
还是根据前面的词预测下一个词,如上图,把t-1、t-2、t-3这样低维的向量拼接在一起形成一个更高维的向量,然后经过非线性去预测下一个词。
首先将每个词与一个低维度的向量联系起来,即找到这个词的向量表示
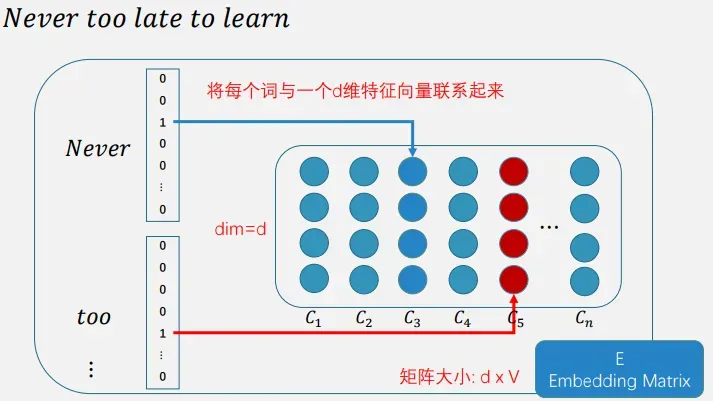
然后对找出来的前文的响亮的词进行拼接,非线性变换,map,然后就得到下一个词的概率。
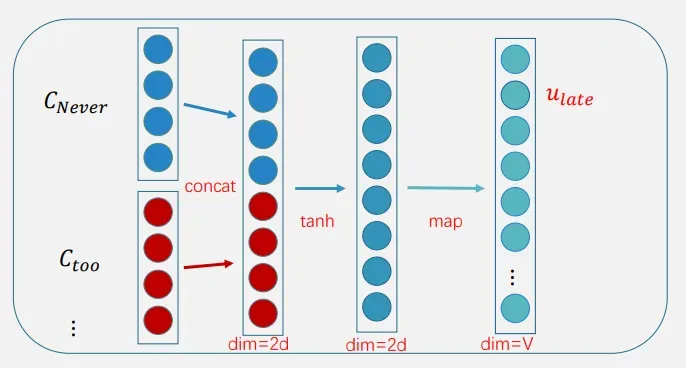
双曲正切函数 (tanh)
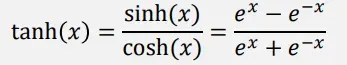
非线性函数,函数值在【−1,1】 , 图像如下
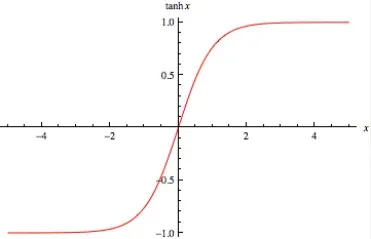
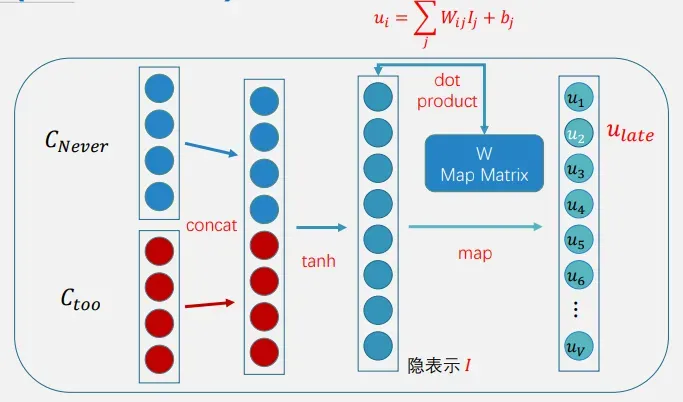
非线性变换之后要乘以一个映射矩阵加上偏置,得到不同词上的取值。
此时还没有得到下一个词的概率,需要进行softmax进行预测

损失计算 – 交叉熵损失函数


然后可以通过链式法则计算交叉熵损失函数的梯度值,进行反向传播。
可以使用随机梯度下降 (SGD) 等优化算法,训练某个权值𝑊𝑖𝑗来减小损失。同样的,可以对神经模型中各层的参数进行优化。
2.3 神经语言模型的挑战
词表可能会非常大,包含几万甚至几十万个不同的单词
参数过多
查询表 (词嵌入矩阵)
映射矩阵
计算量过大
非线性操作 (tanh)
每步都对每个词做softmax:假设词表中含有10万个单词,每一步都要计算10万次条件概率
word2vec可以作为解决问题的一个选择
三、*词嵌入 Word2vec
Word2vec使用浅层网络学习每个词的分布式向量表示
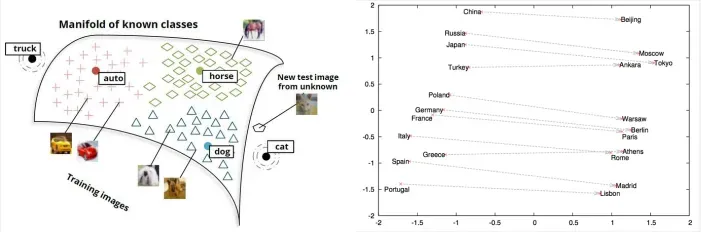
词向量可以捕捉复杂语义关系,例如
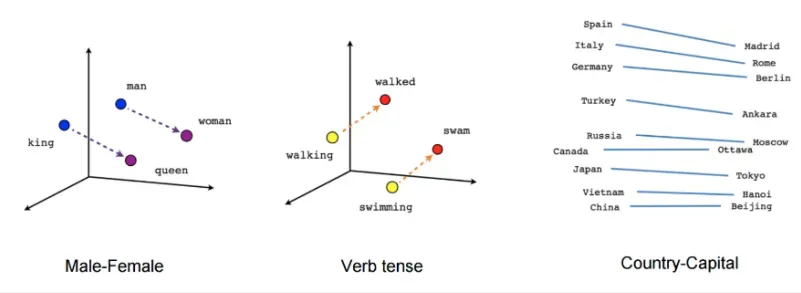
依旧是低维的稠密向量,思想来源于事物在人脑中的表示:分散在不同的神经元上,激活抑制的状态。单独的一个神经元激活或者一致的状态或许没什么用,但这些神经元组合在一起的激活抑制的状态所形成的低维的向量才有意义(组成某个词/句子意思等)
上图我们可以看到比较有意思的一幕,以最右侧国家和首都为例,国家都在左边,首都都在右边,且距离相近,连线也都基本平行。像左边一些表达性别、动词时态等的词也是一样,我们发现存在关系的一些词,在向量空间上也存在着一定的联系。
甚至可以这样计算:
WR(China) − WR(Beijing) ≃ WR(Japan) – WR(Tokyo)
WR(Man) ≃ WR(King) − WR(Queen) + WR(Woman)
WR(Swimming) ≃ WR(Walking) − WR(Walk) + WR(Swim)

又或者 向量German和向量airlines相加,得到的结果和他们的航空公交公司很像…
3.1 典型模型
Word2vec可以采用两种典型结构来获取词的分布式表示
连续词袋模型 (Continuous Bag-of-Words),CBOW
Skip-gram模型
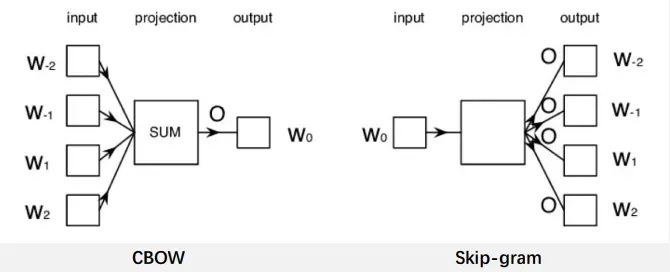
word2vec使用一个固定大小的窗口沿着句子滑动
在每一个窗口中,中间的词作为目标词,其他的词作为上下文
给出上下文词(前后的词),CBOW模型可以预测目标词(中间词)的概率
给出目标词(中间词),skip-gram模型可以预测上下文词(前后的词)的概率
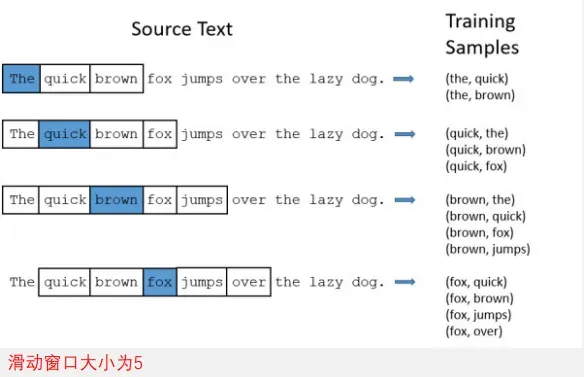
3.1.1 连续词袋模型,CBOW
在CBOW中,给出窗口中上下文的词,模型可以预测目标词
词袋假设:上下文词的顺序不影响模型的预测结果
假设窗口大小为5:��𝑒𝑣𝑒𝑟 𝑡𝑜𝑜 𝑙𝑎𝑡𝑒 𝑡𝑜 𝑙𝑒𝑎𝑟𝑛 ⇒ 𝑃(𝑙𝑎𝑡𝑒|[𝑛𝑒𝑣𝑒𝑟,𝑡𝑜𝑜,𝑡𝑜, 𝑙𝑒𝑎𝑟𝑛])
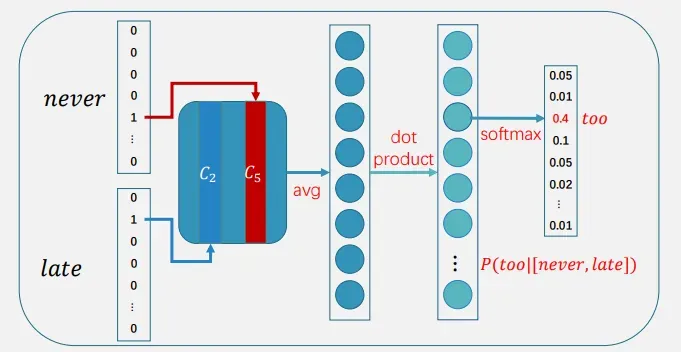
之前是把单独的词向量拿出来怕拼接在一起,现在是加在一起取平均。降低了向量维度。
然后这个“上下文平均向量”再与目标词(too)向量求点积,softmax,得到概率。
3.1.2 Skip-gram模型
在skip-gram架构中,模型通过窗口中的目标词预测上下文的词
假设窗口大小为5
𝑁𝑒𝑣𝑒𝑟 𝑡𝑜𝑜 𝑙𝑎𝑡𝑒 𝑡𝑜 𝑙𝑒𝑎𝑟𝑛
𝑃([𝑡𝑜𝑜, 𝑙𝑎𝑡𝑒]|𝑁𝑒𝑣𝑒𝑟), never去预测too,never去预测late
窗口继续滑动,𝑃([𝑁𝑒𝑣𝑒𝑟, 𝑙𝑎𝑡𝑒,𝑡𝑜]|𝑡𝑜𝑜), …
Skip-gram每一步预测一个上下文词,训练样例为
𝑃(𝑡𝑜𝑜|𝑁𝑒𝑣𝑒𝑟), 𝑃(𝑙𝑎𝑡𝑒|𝑁𝑒𝑣𝑒𝑟), 𝑃(𝑁𝑒𝑣𝑒𝑟|𝑡𝑜𝑜), 𝑃(𝑙𝑎𝑡𝑒|𝑡𝑜𝑜), 𝑃(𝑡𝑜|𝑡𝑜𝑜), …
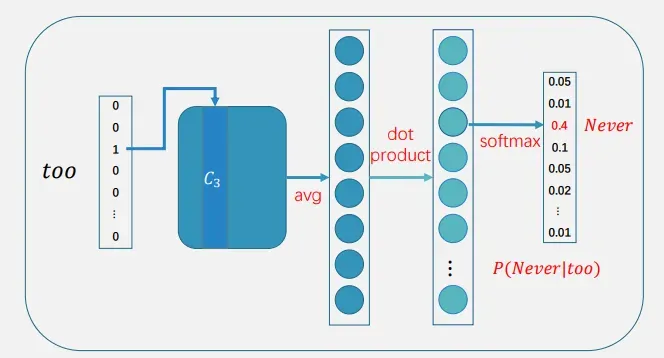
3.1.3 CBOW和Skip-gram
用softmax函数进行预测
用交叉熵损失函数衡量预测与真实分布之间的差异
最终用优化算法学习词向量和映射矩阵
完全softmax存在的问题
当词表过大时
每一步都对所有词做softmax,需要大量计算
需要提高计算的效率
word2vec中对此提出两个改进方案
负采样
分级softmax
3.1.4 负采样
词表通常很大,意味着模型在每一步都需要对大量参数进行更新
负采样在每一步中只选择较小比例的噪声词,对其词向量进行更新
将噪声词从目标词的上下文中区别开,专注于学习高质量的词向量
根据已有词表和已知上下文词,可以根据以下公式计算概率,随机选取一些不在上下文中的词
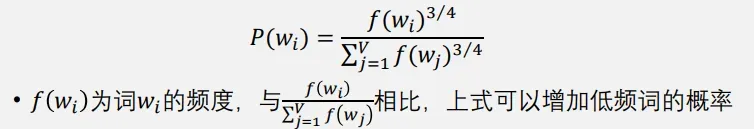
如果词𝑤𝑖 出现在词 𝑤𝑗 的上下文,那么词 𝑤𝑗 的表示相比于其他词的表示,应该更接近于词𝑤𝑖的表示
如下是skip-gram模型训练中的一步,如果不使用负采样,那么输出层中会计算所有词的概率,dim=V
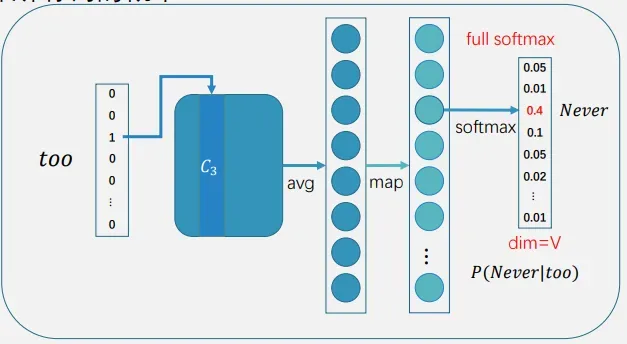
如果使用负采样,假设我们采样了4个负例,dim=5,点积时只需要和这5个点积就行了
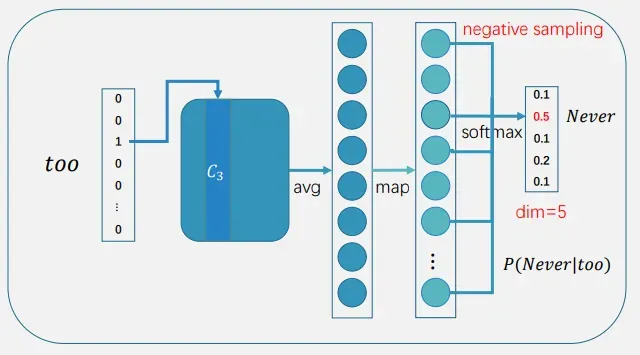
然后,我们可以在每一步计算损失,再优化参数 (无需优化全部参数)
假设参数矩阵大小为300 × 10,000,输出向量长度为5
使用负采样,仅需要更新300 × 5个参数,数量仅占全部参数的0.05%
3.1.5 分级softmax
分级softmax使用Huffman树,按词频对每一个词进行分组,将每一步的计算量由𝑉减小到log𝑉
一个词的概率可以按如下方式计算
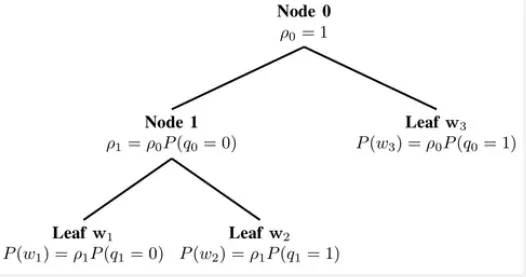
3.2 其他词嵌入的技巧
下采样 根据低频词更可能携带关键信息的假设,下采样按以下概率丢弃一个词,不学习和更新它的向量
![]()
𝑓(𝑤)为词频,𝑡为一个可调整的阈值
Soft滑动窗口 假设滑动窗口对较远的词权值应该更小
将滑动窗口的最大长度定义为𝑆𝑚𝑎𝑥,对每一个训练样例,实际的长度在1和𝑆𝑚𝑎𝑥间随机选择(近的词出现的多,正态分布)
由此,靠近目标词的一些词更有可能出现在窗口中
3.3 其他词向量模型:GloVe
全局向量 (GloVe) 模型采用一种无监督学习的算法,来获取每一个词的向量表示
GloVe模型目的在于将基于统计的矩阵分解(前者是滑动窗口)和基于上下文的skip-gram模型结合在一起
GloVe模型的主要思想是:词共现概率某种程度上暗含了该词的语义信息
Jeffrey Pennington, R Socher, CD Manning. GloVe: Global Vectors for Word Representation. EMNLP 2014
3.4 评估
3.4.1 类比推理
Google类比推理评测数据集
词对间的一种可能的类推关系: a:a* :: b:b* (a之于a* 如 b之于b*)
例如:Tokyo之于Japan 相当于 Paris之于France
14种关系 (其中9种词法,5种语义)
首都;货币;反义 …

如上图,根据Athens和Greece的关系推断Beijing和?的关系。
a*-a=b*-b =》 a*=b*-b+a
Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Efficient estimation of word representations in vector space. In Proceedings of International Conference on Learning Representations (ICLR).
3.4.2 词相似度
WordSimilarity-353 (WordSim353)
人工标注353对英语词的相似度

评估指标: Spearman相关性系数,模型计算词对相似度与人工标注词对相似度的相关性系数
Spearman相关性系数:一个无参数的排序相关性评估 (两组排序变量之间的统计独立性)
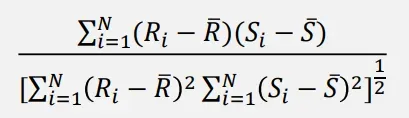
Model1:-0.5,Model2: 1.0
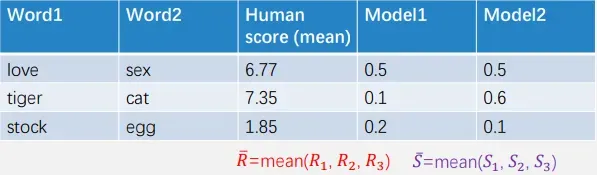
Finkelstein et al. Placing Search in Context: The Concept Revisited, ACM Transactions on Information Systems, 2002
文章出处登录后可见!
