内容

1.引言

2.激活函数类

2.1 Sigmoid

2.1.1 表达式与图像

2.1.2 优缺点

2.2 Tanh

2.2.1 表达式与图像

2.2.2 优缺点

2.3 Relu

2.3.1 表达式与图像

2.3.2 优缺点

2.4 Elu

2.4.1 表达式与图像

2.4.2 优缺点

3. 激活函数的选取

1.引言

上一篇文章我们提到了神经网络中前向传播中数据经过线性变换后会传入一个激活函数(activation function),以满足我们解决非线性问题的需求。

2.激活函数类

有四种常见的激活函数。

2.1 Sigmoid

2.1.1 表达式与图像

表达：

图片：

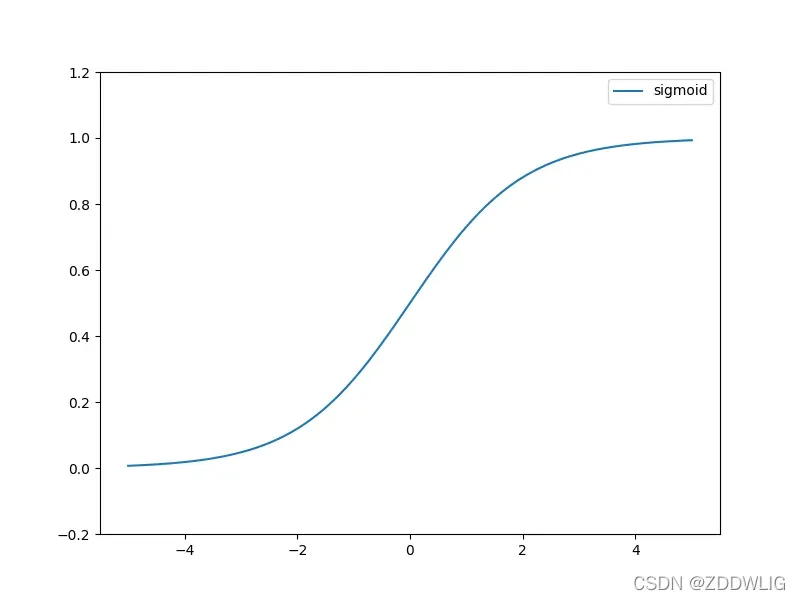
2.1.2 优缺点

优势：

1. 将整个实轴映射到区间，输出值适合作为下一层的输入值。

缺点：

1. 由于该函数的导数最大值只有0.25，经过一层梯度值变为原来的四分之一，经过多层后梯度值会变得越来越接近0，在反向传播时容易出现梯度消失。
2. 该函数图像不关于原点中心对称，称为不是0-均值的(zero-centered),会导致经过一层后梯度值同正或者同负，会使收敛缓慢。
3. 函数表达式包含指数，计算速度比较慢，训练时间长。

2.2 Tanh

2.2.1 表达式与图像

表达：

图片：

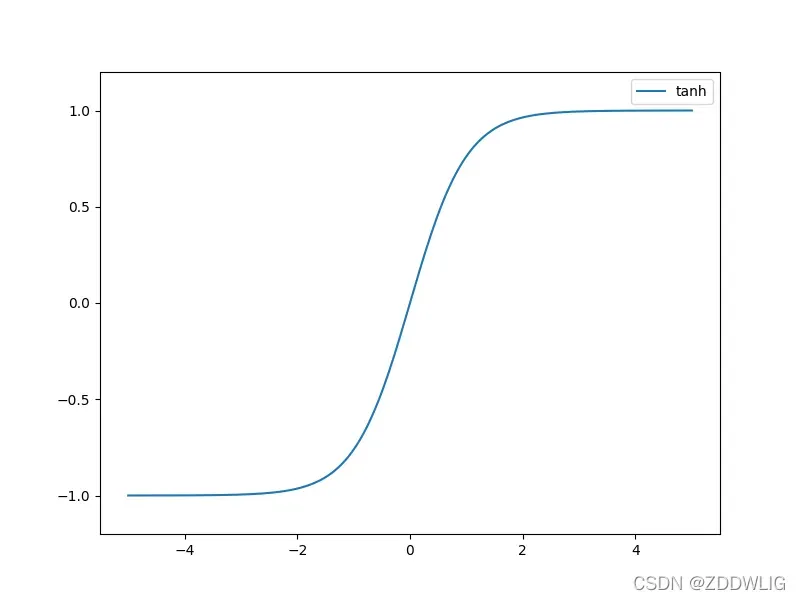
2.2.2 优缺点

优势：

1. 修正了Sigmoid函数非0-均值的问题。

缺点：

1. 爆炸梯度和消失梯度的线性仍然存在。
2. 运输缓慢

2.3 Relu

2.3.1 表达式与图像

表达：

图片：

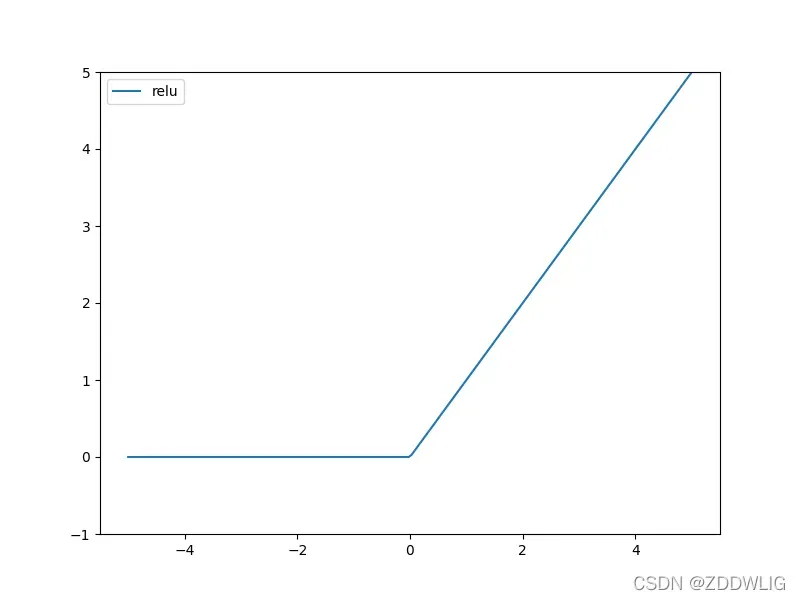
2.3.2 优缺点

优势：

1. 不存在梯度消失现象
2. 简单的表达式和快速的计算

缺点：

1. 非0-均值的
2. 为不可导点，但是可以采用次梯度(sub-gradient)解决
3. 由于该函数负半轴恒为0，参数设置不当可能会导致部分神经元的值始终不发生改变，该现象称为神经元死亡(Dead ReLU Problem)

2.4 Elu

2.4.1 表达式与图像

表达：

图片：

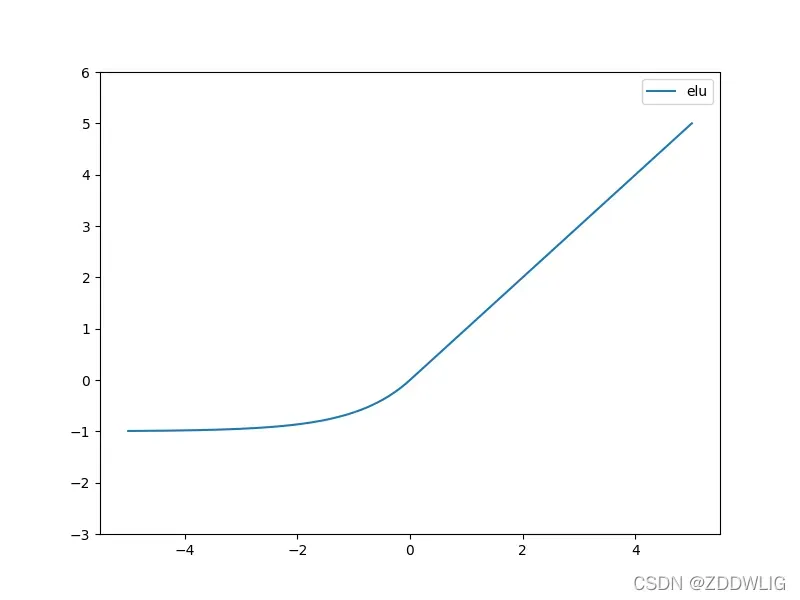
2.4.2 优缺点

优势：

1. 近似0-均值的
2. 避免神经元死亡

缺点：

1. 包含指数，计算速度稍慢

3. 激活函数的选取

那么我们如何选择激活函数呢？

首先，深度学习中我们一般不选取Sigmoid函数，Tanh函数倒是可以一试，通常使用Relu函数或者Elu函数，因为它们收敛速度较快。

其次，要注意的是，如果选取Relu函数一定要选择合适的学习率(learning rate)

总的来说，我们要根据数据特点尽量选择收敛速度快的，0-均值的激活函数。