一、激活函数的含义:
下面简单介绍一下什么是激活函数~
单神经元模型如下图所示: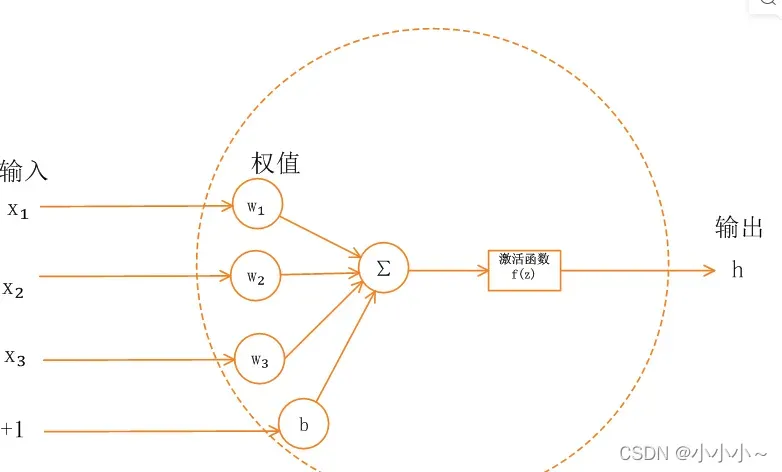
神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值,并将输入值传递给下一层,输入层神经元节点会直接将输入属性值传递给下一层。一层(隐藏或输出)。在多层神经网络中,上层节点的输出与下层节点的输入之间存在函数关系,称为激活函数(也称为激活函数)。
现在让我们进入正题。激活函数的含义是什么?为什么不直接连接神经元的输入和输出呢?
如果不用激励函数(其实相当于激励函数是f(x) = x),在这种情况下你每一层节点的输入都是上层输出的线性函数,很容易验证,无论你神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,这种情况就是最原始的感知机(Perceptron)了,那么网络的逼近能力就相当有限。正因为上面的原因,我们决定引入非线性函数作为激励函数,使用激活函数是为了让中间输出多样化,能够处理更复杂的问题,这样深层神经网络表达能力就更加强大(不再是输入的线性组合,而是几乎可以逼近任意函数)。有论文中把激活函数定义为一个几乎处处可微的函数f: R->R
所以,激活函数就是让网络有更强的性能能力。为什么有这么多激活函数?
随着神经网络的不断发展,逐渐发现过早的激活函数会导致模型收敛较慢,甚至导致不收敛。下面简单介绍一下常用的激活函数及其优缺点。在介绍之前,先介绍一下基本概念:
饱和:
当函数f(x)满足:
称为右饱和度;
当函数f(x)满足:
称为左饱和。
当f(x)同时满足左饱和及右饱和时,称为饱和。
软包和硬包和:
在饱和定义的基础上,如果存在常数c1,当x>c1时候恒满足称之为右硬饱和;同样的,如果存在c2,当x
1. Sigmoid 函数
函数公式如下:
,
它的导数是: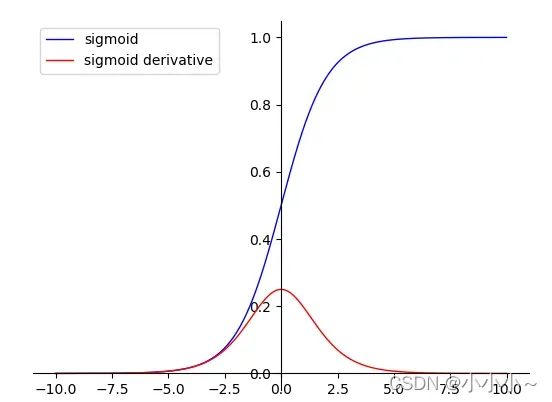
def sigmoid(x):
y = 1/(1+np.exp(-x))
return y
优势:
<1> Sigmoid的取值范围在(0, 1),而且是单调递增,比较容易优化
<2> Sigmoid求导比较容易,可以直接推导得出。
缺点:
<1> Sigmoid函数收敛比较缓慢
<2> 由于Sigmoid是软饱和,容易产生梯度消失,对于深度网络训练不太适合(从图上sigmoid的导数可以看出当x趋于无穷大的时候,也会使导数趋于0)
<3> Sigmoid函数并不是以(0,0)为中心点
2. Tanh函数
函数公式:
它的导数是: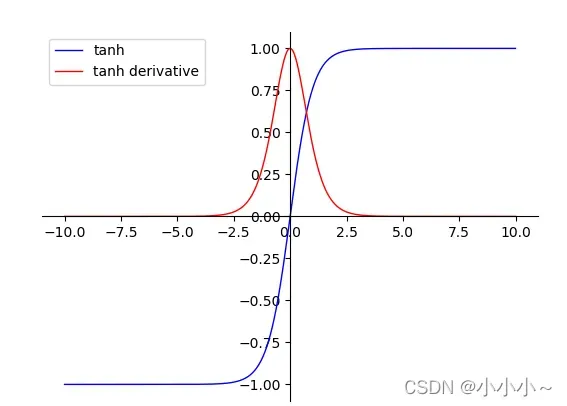
def tanh(x):
y = (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))
return y
优势:
<1> 函数输出以(0,0)为中心
<2> 收敛速度相对于Sigmoid更快
缺点:
<1> tanh并没有解决sigmoid梯度消失的问题
3. ReLU函数
公式如下:
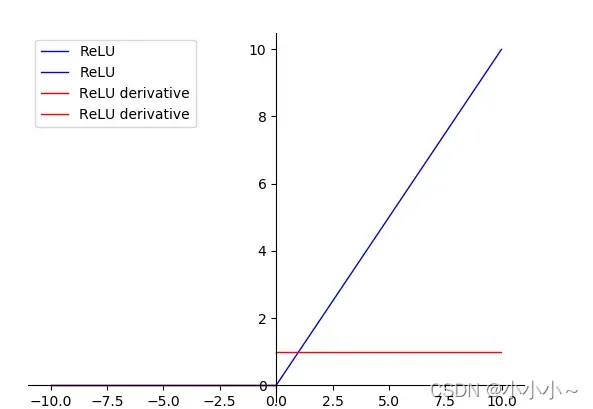
def ReLU(x):
y = []
for i in x:
if i >= 0:
y.append(i)
else:
y.append(0)
return y
优势:
<1> 在SGD中收敛速度要比Sigmoid和tanh快很多
<2> 有效的缓解了梯度消失问题
<3> 对神经网络可以使用稀疏表达
<4> 对于无监督学习,也能获得很好的效果
缺点:
<1> 在训练过程中容易杀死神经元,造成梯度消失0的情况。比如一个特别大的梯度经过神经元之后,我们调整权重参数,就会造成这个ReLU神经元对后来来的输入永远都不会被激活,这个神经元的梯度永远都会是0。
4.LReLU函数
公式:
LReLU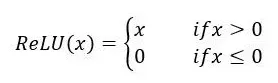
LRelu的优点:缓解了Relu神经元死亡的问题。
def LReLU(x):
y = []
for i in x:
if i >= 0:
y.append(i)
else:
y.append(0.01*i)
return y
LRelu/PReLU的优点:
优势:
<1> .解决了正区间梯度消失问题;
<2> .易于计算;
<3> .收敛速度快;
<4> .解决了某些神经元不能被激活
缺点:
<1> 输出不是以零为中心
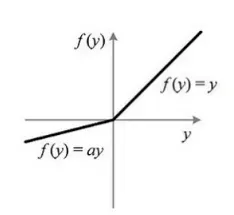
4.PReLU函数
公式:
PReLU
其中是可以学习的。如果
,那么 PReLU 退化为ReLU;如果
是一个很小的固定值(如
),则 PReLU 退化为 Leaky ReLU(LReLU)。
PReLU 只增加了极少量的参数,也就意味着网络的计算量以及过拟合的危险性都只增加了一点点。特别的,当不同 channels 使用相同的a时,参数就更少了。BP 更新a时,采用的是带动量的更新方式(momentum)
功能太多了,以后继续补充!
文章出处登录后可见!
