1. AI技术聚合首页
  2. 技术文章

【Sensor Fusion】相机标定（理论推导+具体实现）

心中带点小风骚 • • 技术文章 • 阅读 447

内容

为什么要进行相机校准

相机标定原理推导

坐标系变换

世界坐标系 -> 相机坐标系

相机坐标系 -> 图像坐标系

图像坐标系 -> 像素坐标系

为什么使用齐次坐标系

图像失真和失真校正

径向畸变

切向畸变

相机内参和外参的应用

相机标定具体实现

步：

1. 准备标定图片

2. 对每张标定图片，提取角点信息

3. 对每张标定图片，进一步提取亚像素角点信息

4. 在标定图上绘制找到的内角点

5. 相机标定

6. 利用标定结果对测试图进行矫正

完整代码(python+opencv)：

参考

为什么要进行相机校准

首先谈谈相机为什么需要标定？任何理论物理模型都是在特定假设上对真实事物的近似，然而在实际应用中存在误差。实际应用中，普通相机成像误差的主要来源有两部分，第一是sensor制造产生的误差，比如sensor成像单元不是正方形，sensor歪斜；第二是镜头制造和安装产生的误差，镜头一般存在非线性的径向畸变；镜头与相机sensor安装不平行，还会产生切向畸变。

为了确定物体表面上一点的三维几何位置与其在图像中的对应点之间的关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数情况下，这些参数必须通过实验和计算获得。这种求解参数的过程称为相机标定（或相机标定）。标定结果的准确性和算法的稳定性直接影响相机工作产生的结果的准确性。 .

相机标定方法包括自标定（寻找图像中的特征点）和标定板标定（特征点容易找到且稳定性好）。一般使用校准板进行校准。相机标定根据相机是否静止可分为静态相机标定（标定板移动，相机静止）和动态相机标定（标定板静止，相机移动）。

相机标定原理推导

坐标系变换

坐标系转换是将空间的三维世界坐标系转换为图像处理的二维像素坐标系。坐标系包括：世界坐标系、相机坐标系、图像坐标系、像素坐标系。

世界坐标系（world coordinate）(xw,yw,zw)：是实际物体再三维世界中的坐标系，可以表示任何物体，是由于相机而引入的。单位m。

相机坐标系（camera coordinate）(xc,yc,zc)：是一个三维直角坐标系，以摄像机光心为原点，z轴与光轴重合也就是z轴指向相机的前方（也就是与成像平面垂直），x轴与y轴的正方向与物体坐标系平行。

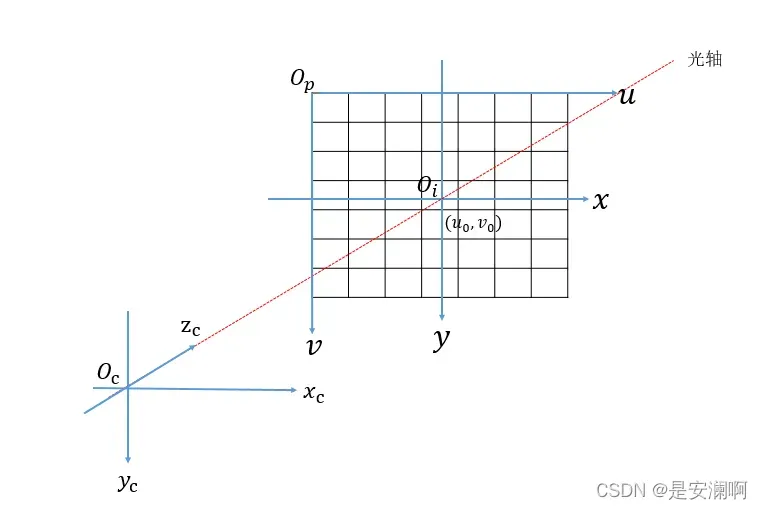
【Sensor Fusion】相机标定（理论推导+具体实现）

图像坐标系（也叫平面坐标系）(image coordinate)(x,y)：是像平面上的二维直角坐标系。坐标原点为摄像机光轴与图像物理坐标系的交点位置。它的x轴与相机坐标系的xc轴平行，它的y轴与相机坐标系的yc轴平行，单位是mm。

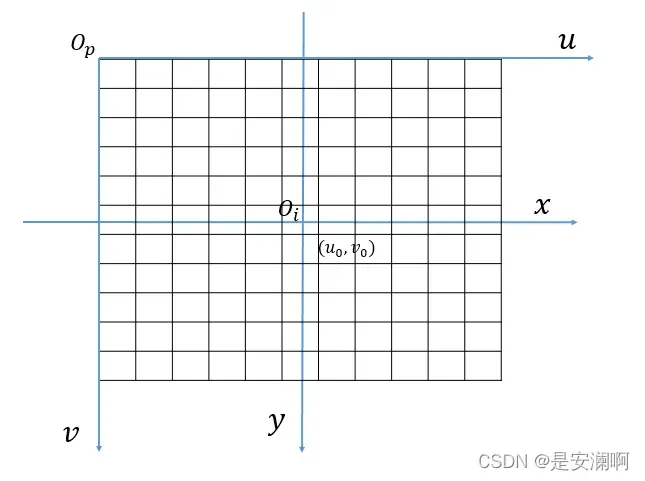
【Sensor Fusion】相机标定（理论推导+具体实现）

像素坐标系：（pixel coordinate）(u,v)，以像素为单位，坐标原点在左上角。像素坐标系到平面坐标系涉及到的是单位的转换和平移。传感器以mm单位到像素中间有转换。举个例子，CCD传感上上面的8mm x 6mm，转换到像素大小是640×480。dx，dy表示像素坐标系中每个像素的物理大小。像素坐标系的x轴与图像坐标系的u轴平行，像素坐标系的y轴与图像坐标系的v轴平行。

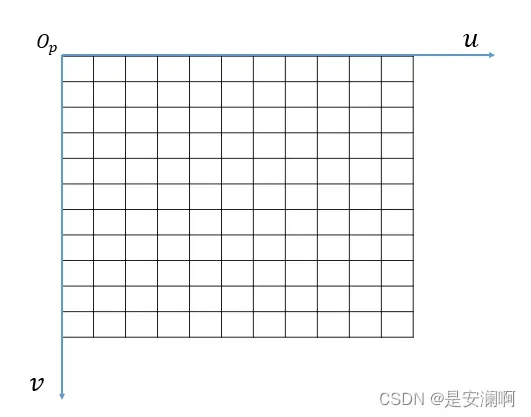
【Sensor Fusion】相机标定（理论推导+具体实现）

世界坐标系 -> 相机坐标系

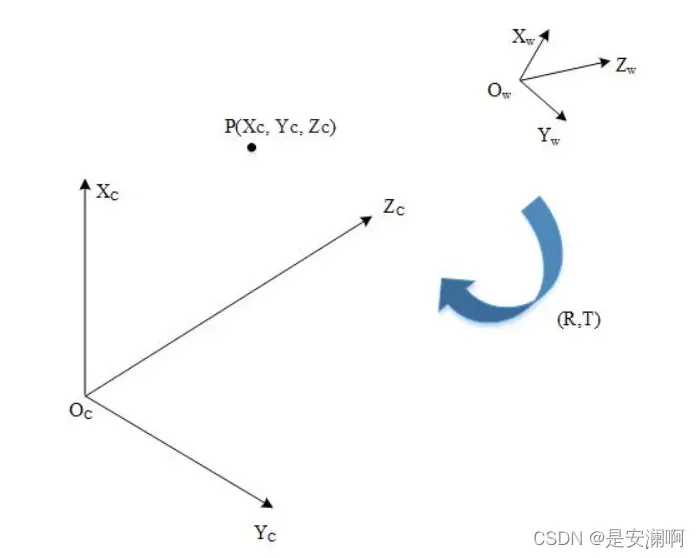
【Sensor Fusion】相机标定（理论推导+具体实现）

相机坐标系以相机位置为原点，世界坐标系以物体中心为原点。世界坐标系到相机坐标系的转换包括x,y,z三个轴的平移，用T表示；因为相机不一定与物体平齐，所以坐标变换还包括以x,y,z轴为轴的旋转，用R表示。

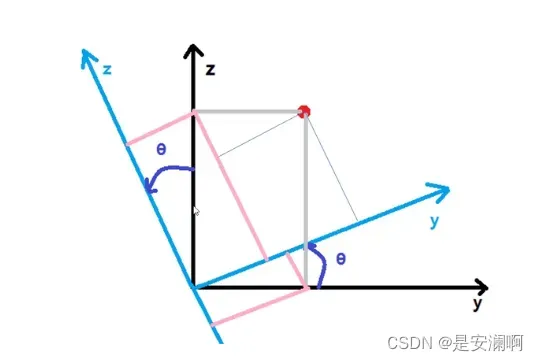
【Sensor Fusion】相机标定（理论推导+具体实现）

红点为世界坐标系中的P(x_{w},y_{w},z_{w})点，黑色为世界坐标系，蓝色为相机坐标系；绕x轴旋转后，通过相似三角形定理：

x_{c}=x_{w}

y_{c}=y_{w}cos\theta+z_{w}sin\theta

z_{c}=z_{w}cos\theta-y_{w}sin\theta

写成矩阵形式：

\begin{bmatrix}x_{c}\\y_{c}\\z_{c} \end{}=\begin{bmatrix}1&0&0\\0&cos\theta&sin\theta\\0&-sin\theta&cos\theta \end{}\begin{bmatrix} x_{w}\\y_{w}\\z_{w}\end{}

同样，绕y轴旋转后：

\begin{bmatrix}x_{c}\\y_{c}\\z_{c} \end{}=\begin{bmatrix}0&cos\theta&-sin\theta\\0&1&0\\0&sin\theta&cos\theta\end{}\begin{bmatrix} x_{w}\\y_{w}\\z_{w}\end{}

绕z轴旋转后：

\begin{bmatrix}x_{c}\\y_{c}\\z_{c} \end{}=\begin{bmatrix}cos\theta&sin\theta&0\\-sin\theta&cos\theta&0\\0&0&1\end{}\begin{bmatrix} x_{w}\\y_{w}\\z_{w}\end{}

因此，世界坐标系与相机坐标系的转换可以表示为：

\begin{bmatrix}x_{c}\\y_{c}\\z_{c} \end{}=R\begin{bmatrix} x_{w}\\y_{w}\\z_{w}\end{}+T=\begin{bmatrix}1&0&0\\0&cos\theta&sin\theta\\0&-sin\theta&cos\theta \end{} \begin{bmatrix}0&cos\theta&-sin\theta\\0&1&0\\0&sin\theta&cos\theta\end{} \begin{bmatrix}cos\theta&sin\theta&0\\-sin\theta&cos\theta&0\\0&0&1\end{}\begin{bmatrix}x_{w}\\y_{w}\\z_{w} \end{}+\begin{bmatrix}t_{x}\\t_{y}\\t_{z}\end{}

简化为：

\begin{bmatrix}x_{c}\\y_{c}\\z_{c}\\1 \end{}=\begin{bmatrix}R&T\\0&1 \end{}\begin{bmatrix}x_{w}\\y_{w}\\z_{w}\\1 \end{}

相机坐标系 -> 图像坐标系

相机坐标系到图像坐标系可以利用针孔成像原理推导出来，这涉及到相机本身的参数。

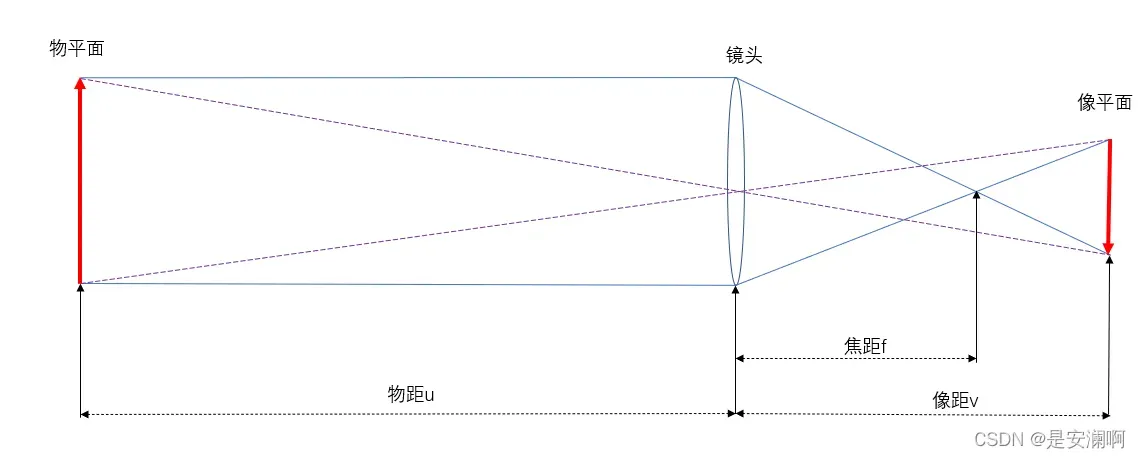
【Sensor Fusion】相机标定（理论推导+具体实现）

为了计算方便，我们将图像的平面对称性进行倒置，如下图所示：

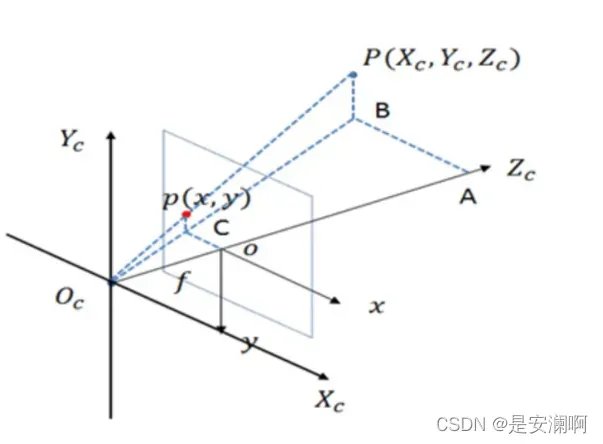
【Sensor Fusion】相机标定（理论推导+具体实现）

点P(x_{c},y_{c},z_{c})是相机坐标系中的一个点，映射到图像坐标系为P(x,y)。通过相似三角形定理，我们可以得到：

\frac{O_{c}O}{O_{c}A}=\frac{OC}{AB}=\frac{f}{z_{c}}=\frac{x}{x_{c}}

\frac{O_{c}O}{O_{c}A}=\frac{PC}{PB}=\frac{f}{z_{c}}=\frac{y}{y_{c}}

O_{c}O=f、f为焦距；

进一步：

xz_{c}=fx_{c}

yz_{c}=fy_{c}

进一步：

z_{c}\begin{pmatrix}x\\y\\1 \end{}=\begin{pmatrix}f&0&0&0\\0&f&0&0\\ 0&0&1&0\end{}\begin{pmatrix} x_{c}\\y_{c}\\z_{c}\\1\end{}

图像坐标系 -> 像素坐标系

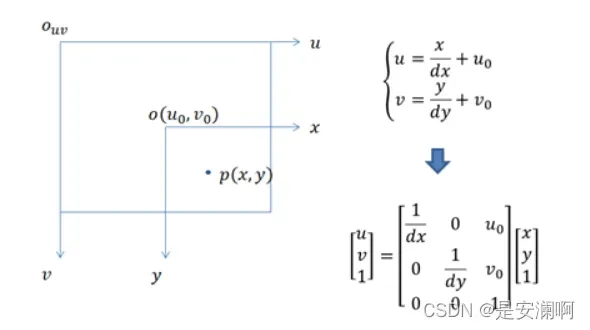
【Sensor Fusion】相机标定（理论推导+具体实现）

图像坐标系到像素坐标系是在x,y轴上的偏移，但是图像坐标系的单位为mm，像素坐标系的单位为像素pt，所以需要进行单位的转换。

假设每个像素所代表的物理尺寸为dx,dy，则：

u=\frac{x}{dx}+u_{0}

v=\frac{y}{dy}+v_{0}

\begin{pmatrix}u\\v\\1 \end{}z_{c}=\begin{pmatrix}\frac{1}{dx}&0&u_{0}\\0&\frac{1}{dy}&v_{0}\\0&0&1\end{}\begin{pmatrix}x\\y\\1 \end{}z_{c}

由此，可以得到像素坐标系与相机坐标系的关系：

\begin{pmatrix}u\\v\\1 \end{}z_{c}=\begin{pmatrix}\frac{1}{dx}&0&u_{0}\\0&\frac{1}{dy}&v_{0}\\0&0&1\end{}\begin{pmatrix}f&0&0&0\\0&f&0&0\\ 0&0&1&0\end{}\begin{pmatrix} x_{c}\\y_{c}\\z_{c}\\1\end{}

这样就可以得到像素坐标系与世界坐标系的关系：

\begin{pmatrix}u\\v\\1 \end{}z_{c}=\begin{pmatrix}\frac{1}{dx}&0&u_{0}\\0&\frac{1}{dy}&v_{0}\\0&0&1\end{}\begin{pmatrix}f&0&0&0\\0&f&0&0\\ 0&0&1&0\end{}\begin{bmatrix}R&T\\0&1 \end{}\begin{bmatrix}x_{w}\\y_{w}\\z_{w}\\1 \end{}

注意：不同的矩阵符号是为了便于区分。

大多数情况下是相机坐标系到像素坐标系的转换：

\begin{pmatrix}u\\v\\1 \end{}z_{c}=\begin{pmatrix}\frac{1}{dx}&0&u_{0}\\0&\frac{1}{dy}&v_{0}\\0&0&1\end{}\begin{pmatrix}f&0&0&0\\0&f&0&0\\ 0&0&1&0\end{}\begin{pmatrix} x_{c}\\y_{c}\\z_{c}\\1\end{}=\begin{pmatrix} \frac{f}{dx}&0&u_{0}&0\\0&\frac{f}{dy}&v_{0}&0\\0&0&1&0\end{}\begin{pmatrix} x_{c}\\y_{c}\\z_{c}\\1\end{}

\frac{f}{dx}为u轴的比例因子，\frac{f}{dy}为v轴的比例因子；

K_1=\begin{pmatrix} \frac{f}{dx}&0&u_{0}&0\\0&\frac{f}{dy}&v_{0}&0\\0&0&1&0\end{};K_2=\begin{pmatrix}R&T\\0&1 \end{}

K_1为相机内参； K_2为相机外参；

所以，像素坐标系 -> 世界坐标系可以表示为：

\begin{pmatrix}u\\v\\1 \end{}z_{c}=K_1K_2\begin{pmatrix} x_{w}\\y_{w}\\z_w\\1\end{}

外参是相机相对于世界坐标系的旋转和平移变换关系。内参是相机的固有属性，即焦距、像素大小。式中有z_c，表示物体到光心的距离。因此，在标定时，如果物体与相机的位置不同，那么我们就必须在不同的位置标定相机。当物体远离相机时，相机上的图像很小，而一个像素所代表的实际尺寸很大。当物体靠近相机时，图像很大，而一个像素所代表的物体的实际尺寸很小。因此，需要校准不同的位置。

为什么使用齐次坐标系

齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射几何变换”—— F.S。Hill, JR。

齐次坐标很容易进行仿射变换。

首先：齐次坐标就是用N+1维来代表N维坐标；

将三维坐标视为列向量，则矩阵*列向量得到的新向量的每个分量都是旧列向量的线性函数，因此三维笛卡尔坐标与矩阵相乘只能实现缩放和三维坐标的总和。旋转，但不是坐标平移。如下：

【Sensor Fusion】相机标定（理论推导+具体实现）

将三维的笛卡尔坐标添加一个额外坐标，就可以实现坐标平移了，而且保持了三维向量与矩阵乘法具有的缩放和旋转操作。这个就称为齐次坐标。而这种变换也称为仿射变换(affine transformation)，不属于线性变换。仿射变换是：“线性变换”+“平移”。

齐次坐标可以用来清楚地区分向量和点。

(9条消息) 深入探索透视投影变换_popy007的博客-CSDN博客_投影变换

图像失真和失真校正

畸变（distortion）是对直线投影（rectilinear projection）的一种偏移。直线投影是场景内的一条直线投影到图片上也保持为一条直线。畸变就是一条直线投影到图片上不能保持为一条直线了，这是一种光学畸变（optical aberration。

图像畸变一般分为径向畸变和切向畸变两种。径向畸变发生在相机坐标系到图像坐标系的转换过程中；切向畸变发生在相机制造过程中，因为感光平面不平行于镜头。

畸变 还有其他类型的畸变，但没有径向畸变，切向畸变是显着的。

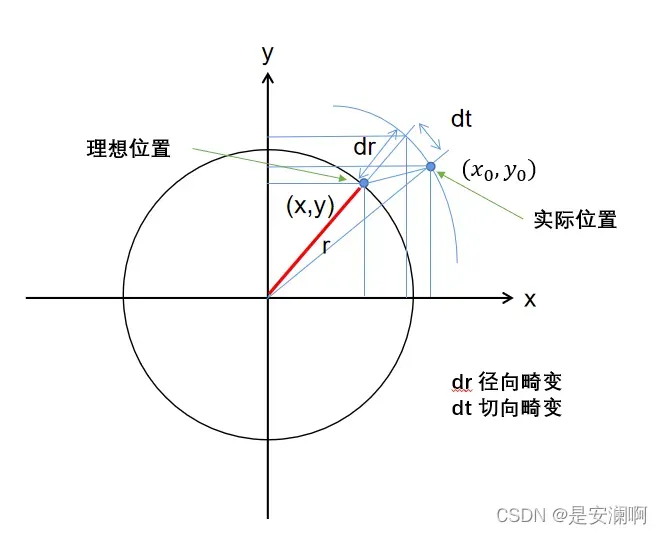
【Sensor Fusion】相机标定（理论推导+具体实现）

径向畸变

【Sensor Fusion】相机标定（理论推导+具体实现）

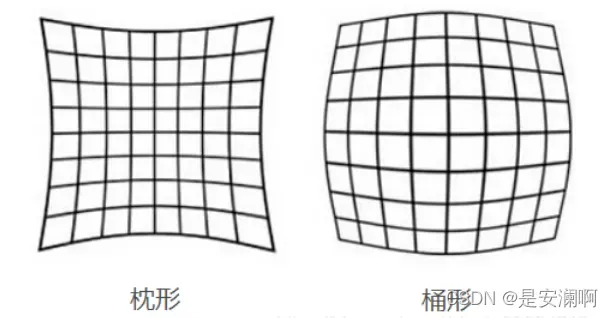
径向畸变（枕形、桶形）：光线在远离镜头中心的地方比靠近中心的地方更弯曲。当光线靠近中心时，畸变较小，当光线沿径向远离中心时，畸变较大。桶形畸变虽然不影响成像清晰度，但会影响成像的位置精度，会给图像分析和图像测量带来误差。

径向畸变随着距中心的距离而增加，因此可以用一个多项式函数来描述畸变前后的坐标变化：

【Sensor Fusion】相机标定（理论推导+具体实现）

注：(k_1,k_2,k_3)为径向畸变系数； (x_0,y_0)是变形后点的坐标，(x,y)是理想点的坐标，r^2=x^2+y^2。

对于畸变较小的图像中心区域，畸变校正主要通过k_1进行；对于畸变较大的边缘区域，主要是k_2工作。根据所使用的镜头，可以适当地使用适当的校正因子。

切向畸变

切向畸变：透镜不完全平行于图像平面，即sensor装配时与镜头间的角度不准。

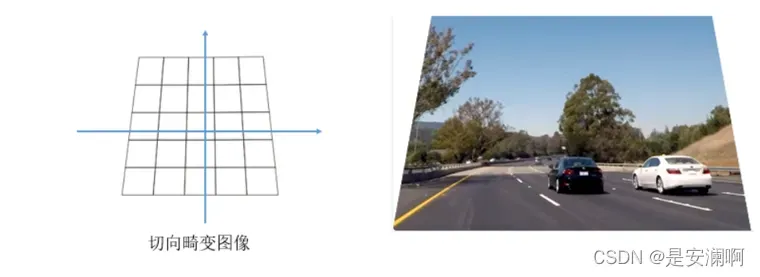
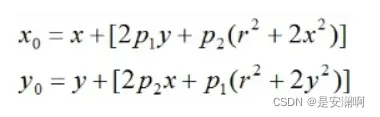
【Sensor Fusion】相机标定（理论推导+具体实现）

【Sensor Fusion】相机标定（理论推导+具体实现）

注：p_1,p_2为切向畸变系数；

综上，我们一共需要5个畸变参数（k1、k2、k3、p1、p2 ）来描述镜头畸变。

在针孔相机模型中，只要确定了相机参数和畸变参数，就可以唯一确定针孔相机模型。这个过程称为“相机校准”。

一旦相机结构确定，包括镜头结构和焦距，我们就可以使用这些参数来近似相机。相机参数标定结果的准确性将直接影响相机工作中产生的结果的准确性。因此，相机标定是后续工作的重要前提。

相机内参和外参的应用

对于单目视觉，在获取内部参数和畸变参数后，可以对捕获的图像进行变换和校正。对捕获的图像进行校正后，对图像进行其他处理。

对于双目视觉，需要使用世界坐标系。在对单目视觉的内参和畸变参数进行校正后，这些变换后的图像可以结合世界坐标系用于定位或其他用途。

相机标定具体实现

使用python+opencv进行相机标定。

步：

1. 准备标定图片（棋盘图）

2. 对每张标定图片，提取角点信息；

3. 对每张标定图片，进一步提取亚像素角点信息；

4. 在标定图上绘制找到的内角点

5. 相机标定(得到相机内外参)

6. 利用标定结果对棋盘图进行矫正

1. 准备标定图片

标定图片需要使用标定板在不同位置、不同角度、不同姿态下拍摄，最少需要3张，以10~20张为宜。标定板需要是黑白相间的矩形构成的棋盘图。

棋盘图PDF文件链接：https://pan.baidu.com/s/1V1nJYyKDd0ZmIM0BtfyTSg
提取码：alth

我做实验的时候用的是别人的照片，我的相机拍出来的照片失真并不明显。非常感谢这位博主，数据集在这里：

链接：https://pan.baidu.com/s/1K1SsxV8H_F5BG0avBdbOiQ
提取码：v6en

【Sensor Fusion】相机标定（理论推导+具体实现）

2. 对每张标定图片，提取角点信息

使用FindChessboardCorners()函数提取角点信息。

【Sensor Fusion】相机标定（理论推导+具体实现）

3. 对每张标定图片，进一步提取亚像素角点信息

使用cornerSubPix函数在角点检测中精确化角点位置。

【Sensor Fusion】相机标定（理论推导+具体实现）

4. 在标定图上绘制找到的内角点

drawChessboardCorners函数用于绘制被成功标定的角点。

【Sensor Fusion】相机标定（理论推导+具体实现）

【Sensor Fusion】相机标定（理论推导+具体实现）

5. 相机标定

获取到棋盘标定图的内角点图像坐标之后，使用calibrateCamera()函数进行标定，计算相机内参和外参系数。

【Sensor Fusion】相机标定（理论推导+具体实现）

6. 利用标定结果对测试图进行矫正

使用undistort()函数对测试的图片进行标定。结果如下图：

【Sensor Fusion】相机标定（理论推导+具体实现）

【Sensor Fusion】相机标定（理论推导+具体实现）

完整代码(python+opencv)：

import argparse
from argparse import RawDescriptionHelpFormatter
from email import parser
import numpy as np
import cv2

def findCorners(img,srcPath,imgId,col,row):
    srcGray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
    ret,corners = cv2.findChessboardCorners(srcGray,(col,row),None)
    if ret:
        criteria = (cv2.TermCriteria_EPS + cv2.TermCriteria_COUNT,10,0.001)
        cornersSubPix = cv2.cornerSubPix(srcGray,corners,(5,5),(-1,-1),criteria)
        savePath = srcPath + "\\" + str(imgId) + "_corner.jpg"
        cv2.drawChessboardCorners(img,(row,col),cornersSubPix,ret)
        cv2.imwrite(savePath,img)
        print("保存找到角点的图像，地址：",savePath)
        return (ret,cornersSubPix)

def camCalibration(imgDir,srcPath,imgNums,row,col):
    w,h = 0,0
    allCornersList = []
    patterns = []
    # 相机标定
    x,y = np.meshgrid(range(row),range(col))
    prod = row * col
    patternPoints = np.hstack((x.reshape(prod,1),y.reshape(prod,1),
                               np.zeros((prod,1)))).astype(np.float32)
    for i in range(1,imgNums+1):
        imgPath = imgDir + "\\" + str(i) + ".jpg"
        print("imgPath:",imgPath)
        # 读取图像
        img = cv2.imread(imgPath)
        (h,w) = img.shape[:2]
        print("(h:w):",(h,w))
        # 提取角点
        ret,cornres = findCorners(img,srcPath,i,row,col)
        if ret:
            allCornersList.append(cornres)
            patterns.append(patternPoints)
            rms,camMatrix,distcoeffs,rvecs,thecs = cv2.calibrateCamera(patterns,allCornersList,(w,h),None,None)
            print("rms:",rms)
            print("distcoeffs:",distcoeffs)
            print("camMatrix:",camMatrix)
            print("rvecs:",rvecs)
            print("thecs:",thecs)
    return (camMatrix,distcoeffs)


def camCorrect(testDir,camMatrix2,distCoffs2):
    for i in range(1,8):
        corrImgPath = testDir + "\\" + str(i) + ".jpg"
        img = cv2.imread(corrImgPath)
        (w1,h1) = img.shape[:2]
        print("(w1,h1):",(w1,h1))
        # 对参数处理，去除不必要的边缘
        newCamMatrix,roi = cv2.getOptimalNewCameraMatrix(camMatrix2,distCoffs2,(w1,h1),1,(w1,h1))
        # 矫正图像
        dst = cv2.undistort(img,camMatrix2,distCoffs2,None,newCamMatrix)
        # 保存校正后的图像
        # x,y,w,h = roi
        # dst = dst[y:y+h,x:x+w]
        corPath = testDir + "\\" + str(i) + "_crct.jpg"
        cv2.imwrite(corPath,dst)
        print("保存校正后的图像，地址：",corPath)
        
        
if __name__ == "__main__":
    parser = argparse.ArgumentParser(formatter_class=RawDescriptionHelpFormatter)
    parser.add_argument("--imgDir",help="标定图片路径",type=str,metavar='',default="E:\\09tmp\\src")
    parser.add_argument("--srcPath",help="图片保存途径",type=str,metavar='',default="E:\\09tmp\\res")  
    parser.add_argument("--testDir",help="待测试图片路径",type=str,metavar='',default="E:\\09tmp\\src")
    parser.add_argument("--row",help="每一行有多少角点,边缘处不算",type=int,metavar='',default="7")
    parser.add_argument("--col",help="每一列有多少角点,边缘处不算",type=int,metavar='',default="4")
    parser.add_argument("--imgNum",help="多少幅图像",type=int,metavar='',default="7")
    args=parser.parse_args()
    # 相机标定
    camMatrix,distCoffs = camCalibration(args.imgDir,args.srcPath,args.imgNum,args.row,args.col)
    # 矫正图片
    camCorrect(args.testDir,camMatrix,distCoffs)

参考

(37 封私信 / 81 条消息) 世界坐标系 – 搜索结果 – 知乎 (zhihu.com)

为什么要相机标定？你想知道的都在这！_坐标系 (sohu.com)

相机参数标定（camera calibration）及标定结果如何使用_Aoulun的博客-CSDN博客_相机标定后如何使用

(37 封私信 / 81 条消息) 如何通俗地讲解「仿射变换」这个概念？ – 知乎 (zhihu.com)

(12条消息) 第三更，单目相机标定实践（完整过程）_Aoulun的博客-CSDN博客

图像处理——相机标定（Camera calibration）_fengye2two的博客-CSDN博客_图像标定

文章出处登录后可见！

已经登录？立即刷新

共计人评分，平均分

到目前为止还没有投票！成为第一位评论此文章。

赞 (0)
心中带点小风骚的头像心中带点小风骚普通用户
0
上一篇 2022年3月23日 下午7:05
下一篇 2022年3月23日 下午7:39

相关推荐