孤立随机森林（Isolation Forest）（Python实现）

内容

1 简介

2 孤立随机森林算法(Random Forest Algorithm)

2.1 算法概述

2.2 原理介绍

2.3 算法步骤

3 参数讲解

4 Python代码实现

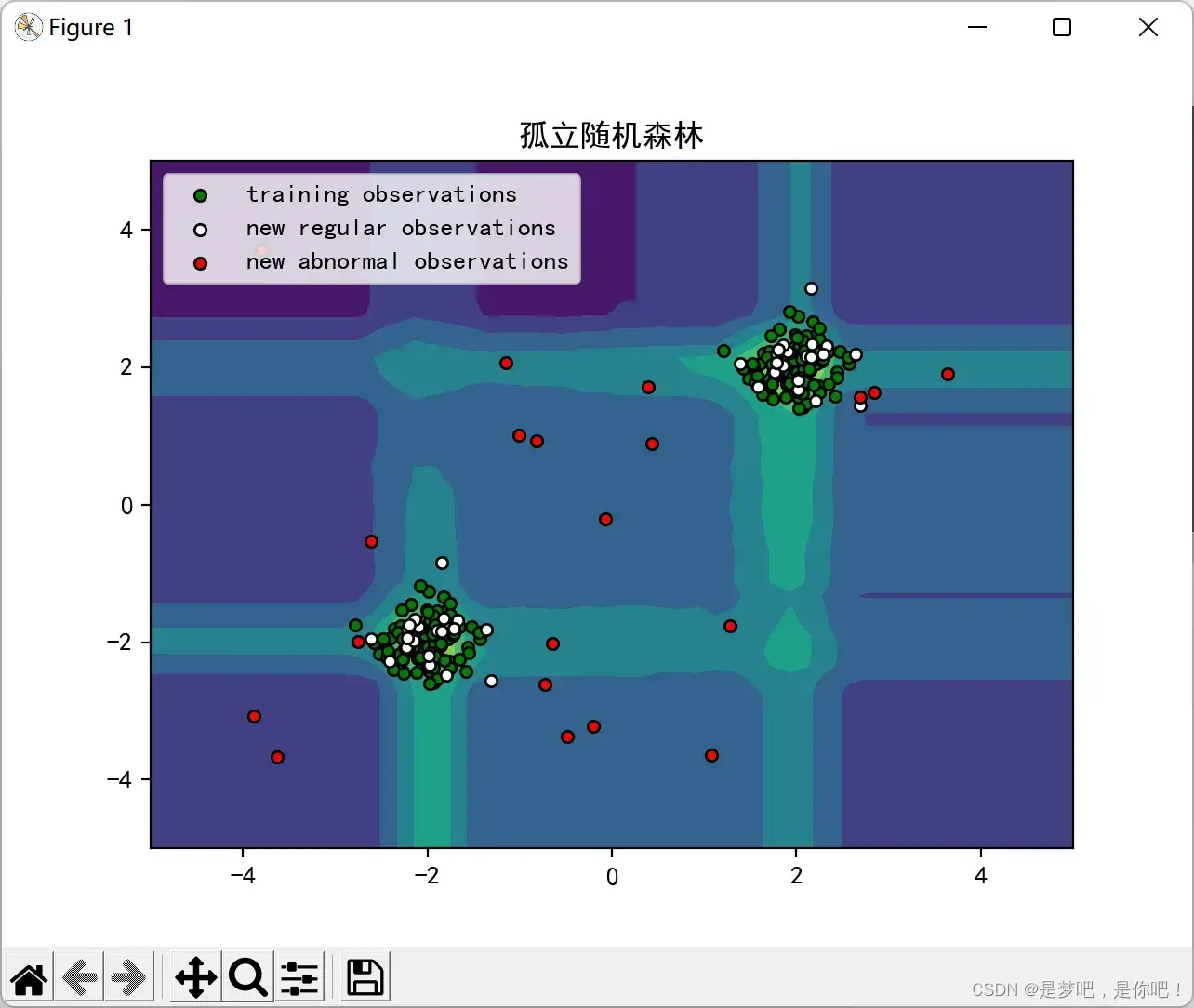
5 结果

1 简介

孤立森林（isolation Forest）是一种高效的异常目标检测算法，它和随机森林类似，但每次选择划分属性和划分点（值）时都是随机的，而不是根据信息增益(Information gain)或基尼指数(Gini index)来选择。

【推荐】电力系统与算法之美

2 孤立随机森林算法(Random Forest Algorithm)

2.1 算法概述

Isolation，意为孤立/隔离，是名词，其动词为isolate，forest是森林，合起来就是“孤立森林”了，也有叫“独异森林”，好像并没有统一的中文叫法。可能大家都习惯用其英文的名字isolation forest，简称iForest 。

iForest算法是由南京大学的周志华和澳大利亚莫纳什大学的Fei Tony Liu，Kai Ming Ting等人共同移除，用于挖掘数据，它是适用于连续数据（Continuous numerical data）的异常目标检测，将异常定义为“容易被孤立的离群点（more likely to be separated）”——可以理解为分布(Distribution)稀疏且离密度高的群体较远的点。用统计学来解释，在数据空间里面，分布(Distribution)稀疏的区域表示数据发生在此区域的概率很低，因此可以认为落在这些区域里的数据是异常的。通常用于网络安全中的攻击目标检测和流(stream)量异常等分析，金融机构则用于挖掘出欺诈行为。对于找出的异常数据，然后要么直接清除异常数据，如数据清理中的去噪(denoising)数据，要么深入分析异常数据，比如分析攻击，欺诈的行为特征。

2.2 原理介绍

iForest 属于Non-parametric和unsupervised的方法，即不用定义数学模型也不需要有标记(token)的训练。对于如何查找哪些点是否容易被孤立（isolated），iForest使用了一套非常高效的策略。假设(Hypothesis)我们用一个随机超平面来切割（split）数据空间（data  space），切一次可以生成两个子空间(Subspace)（详细拿刀切蛋糕一分为二）。之后我们再继续用一个随机超平面来切割每个子空间(Subspace)，循环下去，直到每个子空间(Subspace)里面只有一个数据点为止。直观上来讲，我们可以发现那些密度很高的簇(Cluster)是被切分很多次才会停止切割，但是那些密度很低的点很容易很早就停到一个子空间(Subspace)看了。

iForest 算法得益于随机森林的思想，与随机森林由大量决策树(Decision tree)组成一样，iForest森林也由大量的二叉树组成，iForest 中的树叫 isolation tree，简称 iTree，iTree 树和决策树(Decision tree)不太一样，其构建过程也比决策树(Decision tree)简单，是一个完全随机的过程。

假设(Hypothesis)数据集(Dataset)有 N 条数据，构建一颗 ITree时，从 N条数据中均匀抽样（一般是无放回抽样）出 n 个样本出来，作为这棵树的训练样本。在样本中，随机选出一个特征，并在这个特征的所有值范围内（最小值和最大值之间）随机选一个值，对样本进行二叉划分，将样本中小于该值的划分到节点的左边，大于等于该值的划分到节点的右边。由此得到一个分裂条件和左右两边的数据集(Dataset)，然后分别在左右两边的数据集(Dataset)上重复上面的过程，直到数据集(Dataset)只有一条记录或者达到了树的限定高度。

由于异常数据较小且特征值(eigenvalue)和正常数据差别很大。因此，构建 iTree的时候，异常数据离根更近，而正常数据离根更远。一颗ITree的结果往往不可信，iForest算法通过多次抽样，构建多颗二叉树。最后整合所有树的结果，并取平均深度作为最终的输出深度，由此计算数据点的异常分支。

2.3 算法步骤

怎么来切这个数据空间是iForest的设计核心思想，本文仅学习最基本的方法，由于切割是随机的，所以需要用ensemble的方法来得到一个收敛(Convergence)值（蒙特卡洛方法），即反复从头开始切，然后平均每次切的结果。IForest由 t个iTree（Isolation Tree）孤立树组成，每个iTree是一个二叉树结构，所以下面我们先说一下iTree树的构建，然后再看iForest树的构建。

3 参数讲解

（1）n_estimators：构建多少个itree，int，optional （default=100）指定该森林中生成的随机树数量

（2）max_samples：采样(Sampling)数，自动是256，int，optional（default=’auto）

用于训练随机数的样本数，即下采样(Sampling)(Downsampling)的大小：

1）如果设置的是一个int常数，那么就会从总样本 X 拉取 max_samples个样本生成一棵树  iTree

2）如果设置的是一个float浮点数，那么就会从总样本 X 拉取 max_samples*X.shape[0] 个样本，X.shape[0] 表示总样本个数

3） 如果设置的是 “auto”，则max_samples=min(256, n_samples)，n_samples即总样本的数量

如果max_samples 值比提供的总样本的数量还大的话，所有的样本都会用来构造数，意思就是没有采样(Sampling)了，构造的 n_estimators棵ITree使用的样本都是一样的，即所有的样本。

（3）contamination：c(n)默认是0.1，float in （0， 0.5），optional（default=0.1），取值范围为（0， 0.5），表示异常数据占给定的数据集(Dataset)的比例，就是数据集(Dataset)中污染的数量，定义该参数值的作用是在决策函数中定义阈值(Threshold)。如果设置为“auto”，则决策函数的阈值(Threshold)就和论文一样，在版本0.20中有变换：默认值从0.1变为0.22的auto。

（4）max_features：最大特征数，默认为1，int or float，optional，指定从总样本X中抽取来训练每棵树iTree 的属性的数量，默认只使用一个属性

如果设置为 int 整数，则抽取 max_features 个属性

如果是float浮点数，则抽取 max_features *X.shape[1] 个属性

（5）bootstrap：boolean，optional（default = False），构建Tree时，下次是否替换采样(Sampling)，为True为替换，则各个树可放回地对训练数据进行采样(Sampling)；为False为不替换，即执行不放回的采样(Sampling)

（6）n_jobs：int or None, optional （default = None）， 在运行 fit() 和 predict() 函数时并行运行的作业数量。除了在 joblib.parallel_backend 上下文的情况下，None表示为1，设置为 -1 则表示使用所有可以使用的处理器

（7）behaviour：str，default=’old’，决策函数 decision_function 的行为，可以是“old”和‘new’。设置为 behavior=’new’将会让 decision_function 去迎合其它异常目标检测算法的API，这在未来将会设置为默认值。正如在 offset_ 属性文档中详细解释的那样，decision_function 变得依赖(dependency)于 contamination 参数，以 0 作为其目标检测异常值的自然阈值(Threshold)。

New in version 0.20：behaviour参数添加到了0.20版本中以实现后向兼容

behaviour=’old’在0.20版本中以经弃用，在0.22版本中将不能使用

behaviour参数将在0.22版本中弃用，将在0.24版本中移除

（8）random_state：int，RandomState instance or None，optional（default=None）

如果设置为 int 常数，则该 random_state 参数值是用于随机数生成器(Generator)的种子

如果设置为RandomState实例，则该 random_state 就是一个随机数生成器(Generator)

如果设置为None，则该随机数生成器(Generator)就是使用在 np.random中RandomState实例

（9）verbose：int，optional（default=0）控制树构建过程的冗长性

（10）warm_start：bool，optional（default=False），当设置为TRUE时，重用上一次调用的结果去 fit，添加更多的树到上一次的森林1集合中；否则就 fit一整个新的森林

4 Python代码实现

# _*_coding:utf-8_*_

#~~~~欢迎关注公众号：电力系统与算法之美~~~~~~~·
#~~~~~~~~导入相关库~~~~~~~~~~~·
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
import matplotlib; matplotlib.use('TkAgg')
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
from sklearn.ensemble import IsolationForest  #孤立随机森林

rng = np.random.RandomState(42)  #该方法为np中的伪随机数生成方法，其中的42表示种子，只要种子一致 产生的伪随机数序列即为一致。

#~~~~~~~产生训练数据~~~~~~~~~~
X = 0.3 * rng.randn(100, 2)  #randn：标准正态分布(standard normal distribution)(normal distribution)(Distribution)；rand的随机样本位于[0, 1)中
X_train = np.r_[X + 2, X - 2]
X = 0.3 * rng.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
X_outliers = rng.uniform(low=-4, high=4, size=(20, 2))

#~~~~~~~~~训练模型~~~~~~~~~~~~·
clf = IsolationForest( max_samples=100,random_state=rng, contamination='auto')
clf.fit(X_train)
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_outliers)

xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

#~~~~~~~~~~~~~~~~可视化~~~~~~~~~~~~~~~~~~·
plt.title("孤立随机森林")
plt.contourf(xx, yy, Z, camp=plt.cm.Blues_r)
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='green',
                 s=20, edgecolor='k')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='white',
                 s=20, edgecolor='k')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='red',
                s=20, edgecolor='k')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([b1, b2, c],
           ["training observations",
            "new regular observations", "new abnormal observations"],
           loc="upper left")
plt.show()

5 结果