Attention机制
核心逻辑是“从关注一切到专注”
Attention优点
1、参数少:模型复杂度跟 CNN、RNN 相比,复杂度更小,参数也更少。所以对算力的要求也就更小。
2、速度快:Attention机制每一步计算不依赖于上一步的计算结果,因此可以和CNN一样并行处理。
3、效果好:Attention 是挑重点,从中间抓住重点,不丢失重要的信息。
Soft Attention
这是比较常见的Attention方式,对所有key求权重概率,每个key都有一个对应的权重,是一种全局的计算方式(也可以叫Global Attention)。这种方式比较理性,参考了所有key的内容,再进行加权。但是计算量可能会比较大一些。
Hard Attention
这种方式是直接精准定位到某个key,其余key就都不管了,相当于这个key的概率是1,其余key的概率全部是0。因此这种对齐方式要求很高,要求一步到位,如果没有正确对齐,会带来很大的影响。另一方面,因为不可导,一般需要用强化学习的方法进行训练。(或者使用gumbel softmax之类的)
Local Attention
这种方式其实是以上两种方式的一个折中,对一个窗口区域进行计算。先用Hard方式定位到某个地方,以这个点为中心可以得到一个窗口区域,在这个小区域内用Soft方式来算Attention。
ResNet
ResNet50
感受野计算公式:
是
层对应的感受野,
是
层的卷积核大小,或池化层的池化大小,
是
层的卷积步长或池化步长。
的理论感受野是什么?
,大于输入图像
理论感受野是网络的固有属性。当网络结构确定时,感受野是唯一确定的,与输入图像的大小无关。
筛选
高斯滤波器
线性滤波器,均值滤波导致一个像素会被周围的8个像素“平均”,这个点如果不是噪声点,而是一个边缘,那么是不是就造成了它被“过度”平均了!所以说,需要进行“加权”,让中心像素的权重大一些,周围像素的权重小一些。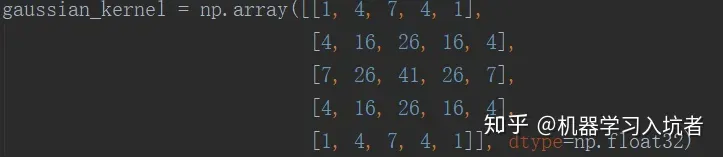
这个就是服从高斯分布的卷积核,可以想象一下高斯分布的形状,就是中间高两边低。这个卷积核最后要除以273(卷积核所有的数值相加等于273)
import cv2
import numpy as np
star_rgb = cv2.imread("lena.jpg")
star_gray = cv2.cvtColor(star_rgb, cv2.COLOR_BGR2GRAY)
def gaussian(image):
"""
Gaussian filter for a RGB image
Args:
image:RGB image
Returns:
filtered image
"""
gaussian_image = np.zeros(shape=image.shape, dtype=np.float32)
gaussian_kernel = np.array([[1, 4, 7, 4, 1],
[4, 16, 26, 16, 4],
[7, 26, 41, 26, 7],
[4, 16, 26, 16, 4],
[1, 4, 7, 4, 1]], dtype=np.float32)
gaussian_kernel = gaussian_kernel / gaussian_kernel.sum()
for i in range(image.shape[0]-5):
for j in range(image.shape[1]-5):
gaussian_image[i+2, j+2] = np.sum(image[i:i+5, j:j+5]*gaussian_kernel)
return gaussian_image.astype(np.uint8)
std_gaussian_star = cv2.GaussianBlur(src=star_gray, ksize=(5, 5), sigmaX=0)
gaussian_star = gaussian(star_gray)
cv2.imshow("original star", star_gray)
cv2.imshow("my gaussian star", gaussian_star)
cv2.imshow("cv2 gaussian star", std_gaussian_star)
cv2.waitKey(0)
均值过滤器
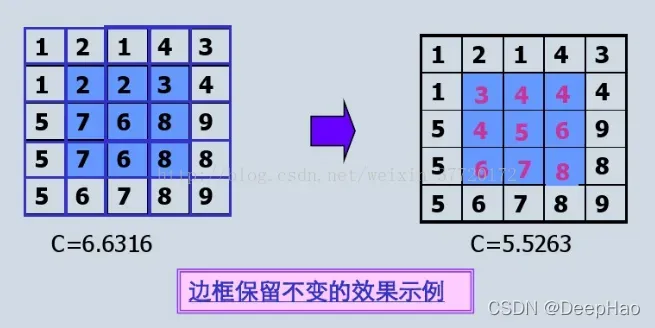
线性滤波器,在图片中的一个正方形区域(通常是),中心点的像素是所有点的像素值的平均值。均值滤波就是对整幅图像进行上述操作。
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
dark_image = np.array(Image.open("dark.jpg").resize((500,700),Image.ANTIALIAS))
gama_image = (dark_image.astype(np.float32)/255)**0.25
def median(image):
"""
median filter for a single RGB image
Args:
image:RGB image
Returns:
filterd image
"""
mean_image = np.zeros(shape=image.shape, dtype=np.float32)
for i in range(image.shape[0]):
for j in range(image.shape[1]):
for k in range(image.shape[2]):
mean_image[i][j][k] = np.mean(image[i:i+2,j:j+2,k])
return mean_image
plt.figure(figsize=(10,10))
plt.subplot(1,3,1)
plt.imshow(dark_image/255)
plt.subplot(1,3,2)
plt.imshow(gama_image)
mean_image=median(gama_image)
plt.subplot(1,3,3)
plt.imshow(mean_image)
中值滤波器
图像中的矩阵,其中
曲面上有个像素,我们对
个像素进行排序,最后将这个矩阵的中心点赋值为九个像素的中值。
最大过滤器和最小过滤器
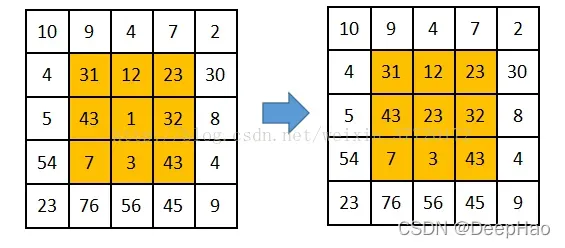
最大最小滤波非线性滤波器,无求和运算。使用最大值而不是中心值会导致中心值更亮;如果使用最小值而不是中心值,则中心值会更暗。如果噪声是胡椒噪声(黑色,低亮度),用最大值代替中心值;如果噪声是盐噪声(白色,高亮度),请使用最小值而不是中心值。
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
dark_image = np.array(Image.open("dark.jpg").resize((500,700),Image.ANTIALIAS))
gama_image = (dark_image.astype(np.float32)/255)**0.25
def max_box(image):
mean_image = np.zeros(shape=image.shape, dtype=np.float32)
for i in range(image.shape[0]):
for j in range(image.shape[1]):
for k in range(image.shape[2]):
mean_image[i][j][k] = np.max(image[i:i+3,j:j+3,k])
return mean_image
plt.figure(figsize=(10,10))
plt.subplot(1,3,1)
plt.imshow(dark_image/255)
plt.subplot(1,3,2)
plt.imshow(gama_image)
mean_image=max_box(gama_image)
plt.subplot(1,3,3)
plt.imshow(mean_image)
plt.show())
1×1卷积核
feature channels线性叠加,进行维度控制,例如在在Inception网络( Going Deeper with Convolutions )中用来降维。
BP与优化器
BP
BP算法即Back propagation,反向传播算法。是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。
反向传播要求有对每个输入值期望得到的已知输出,来计算损失函数的梯度。因此,它通常被认为是一种监督式学习方法,虽然它也用在一些无监督网络(如自动编码器)中。它是多层前馈网络的Delta规则的推广,可以用链式法则对每层迭代计算梯度。反向传播要求人工神经元(或“节点”)的激活函数可微。
优化器
SGD随机梯度下降
随机梯度有两个问题:
1、波动很大,每一次都沿着梯度斜率方向优化,会跳来跳去,收敛速度很慢,如下图
2、学习率需要自己选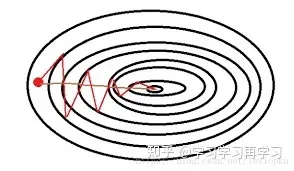
momentum动量梯度下降法
为了解决SGD波动大的问题,这里加入滑动平均,目的是为了能够平滑波动;
所以这里引入一个参数,用来做平滑,
决定了模型的更新速度,
越大,更新越稳定,一般取
或者
,use_nesterov (bool, 可选) – 赋能牛顿动量,默认值False。
velocity=mu∗velocity+gradient
if(use_nesterov):
param=param−(gradient+mu∗velocity)∗learning_rate
else:
param=param−learning_rate∗velocity
、
是历史梯度的一阶反演(原始行进方向),
是当前参数梯度(微调)

RMSprop
在momentum改进了SGD波动过大的问题后,因为momentum采用的是历史梯度一阶导,那是不是历史梯度二阶导也会起作用呢?效果会不会更好呢?、
是历史二阶导,然后用微分平方加权平均数,
是当前参数梯度。这里为了防止分母
为0,所以会加一个很小的数。
Adam
在
然后进行偏差修正:因为移动指数平均会导致迭代开始时与起始值有很大差异,比如一开始行驶的方向有点问题,所以我们需要做几个值以上获得。偏差校正。不得不:
其中,代表迭代次数,除
外,越接近越重要;
YOLOv3损失函数

梯度消失和梯度爆炸及解决方案
渐变消失
目前优化神经网络的方法都是基于BP,即根据损失函数计算的误差通过梯度反向传播的方式,指导深度网络权值的更新优化。其中将误差从末层往前传递的过程需要链式法则(Chain Rule)的帮助,因此反向传播算法可以说是梯度下降在链式法则中的应用。
而链式法则是一个连乘的形式,所以当层数越深的时候,梯度将以指数形式传播。梯度消失问题和梯度爆炸问题一般随着网络层数的增加会变得越来越明显。在根据损失函数计算的误差通过梯度反向传播的方式对深度网络权值进行更新时,得到的梯度值接近0或特别大,也就是梯度消失或爆炸。梯度消失或梯度爆炸在本质原理上其实是一样的。
【梯度消失】经常出现,产生的原因有:一是在深层网络中,二是采用了不合适的损失函数,例如使用sigmoid作为损失函数,其梯度是不可能超过0.25的
【梯度爆炸】一般出现在深层网络和权值初始化值太大的情况下。在深层神经网络或循环神经网络中,误差的梯度可在更新中累积相乘。如果网络层之间的梯度值大于 1.0,那么重复相乘会导致梯度呈指数级增长
梯度爆炸会伴随一些细微的信号,如:①模型不稳定,导致更新过程中的损失出现显著变化;②训练过程中,在极端情况下,权重的值变得非常大,以至于溢出,导致模型损失变成 NaN等等。
解决方案
pre-training+fine-tunning
梯度剪切:对梯度设定阈值【ClipGradByValue,ClipGradByGlobalNorm,ClipGradByNorm】
规范
norm,这是一个带有“距离”概念的函数
L1范数
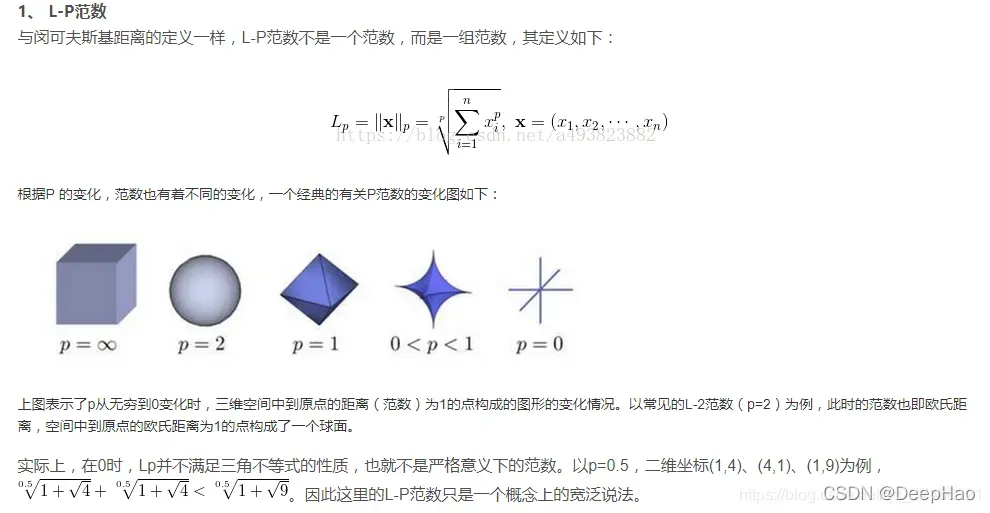
L1范数是我们经常见到的一种范数,它的定义如下,表示向量x中非零元素的绝对值之和:
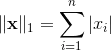
L2范数
L2范数是我们最常见最常用的范数了,我们用的最多的度量距离欧氏距离就是一种L2范数,它的定义如下,表示向量元素的平方和再开平方。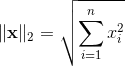
交叉熵
一个事件发生的概率很小,不确定性越大,信息量越大,反之亦然。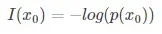
所以你掷硬币,如果它竖起来了,你会说狗屎——这是很多信息。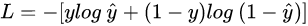
代表grt,
代表预测值
汇集
根据相关理论,特征提取的误差主要来自两个方面:
由于邻域大小有限,估计方差增加;
卷积层参数错误会导致估计均值发生偏移。
一般来说,Average Pooling能减小第一种误差,更多的保留图像的背景信息,Max Pooling能减小第二种误差,更多的保留纹理信息。Average Pooling更强调对整体特征信息进行一层下采样,在减少参数维度的贡献上更大一点,更多的体现在信息的完整传递这个维度上,在一个很大很有代表性的模型中,比如说DenseNet中的模块之间的连接大多采用Average Pooling,在减少维度的同时,更有利信息传递到下一个模块进行特征提取。
BatchNorm
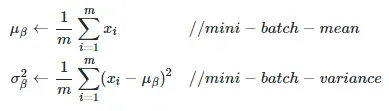

Focal Loss
Focal Loss 就是一个解决分类问题中类别不平衡、分类难度差异的一个 loss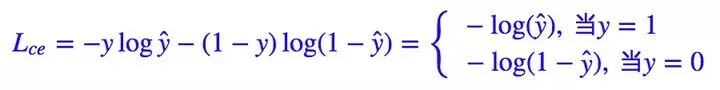
其中是真实标签,
是预测值。当然,对于二分类,我们几乎总是使用
函数来激活
,所以它等价于:
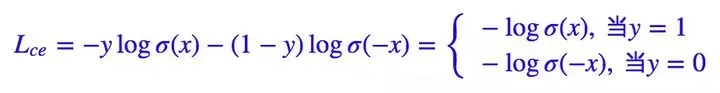
Kaiming 大神的Focal Loss 形式是: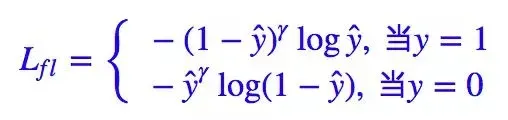
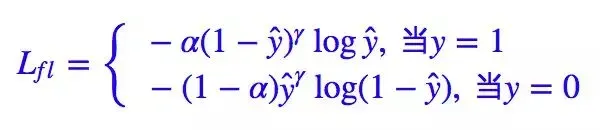
如果实现的预测,则有:
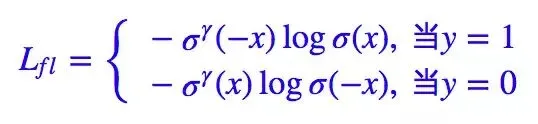
的作用是调整权重曲线的陡峭程度,类别的不平衡本质上在一定程度上导致了分类的难度。例如,如果负样本远多于正样本,那么模型肯定会倾向于有大量的负类。
mAP
TP:被模型预测为正类的正样本
TN:被模型预测为负类的负样本
FP:被模型预测为正类的负样本
FN:被模型预测为负类的正样本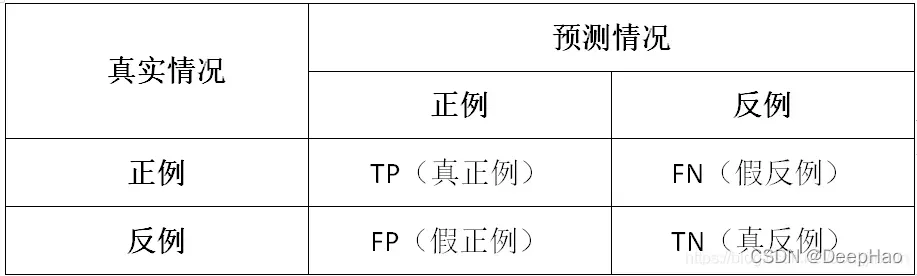
Precision & Recall:假设我们有一组图片,里面有若干待检测的目标,Precision就代表我们模型检测出来的目标有多大比例是真正的目标物体,Recall就代表所有真实的目标有多大比例被我们的模型检测出来了。
TP (True Positive):只考虑预测框的分类和边界坐标,对于一张图片中的某一类别的全部预测框,如果一个预测框与某一个gt (ground truth,真实值) 的IOU大于阈值,即认为这个边界框预测正确,计作一个TP。但是在实际预测中,经常会出现多个预测框与同一个gt的IOU都大于阈值,这时通常只将这些预测框中score最大的算作TP,其它算作FP。
FP (False Positive):对于一张图片中某一类别的所有预测到的边界框,除TP之外的记为FP(不过在实际计算时,因为每个预测框不是TP就是FP,所以一般都只设置一个TP标志位,如果当前预测框预测正确,那么这个标志位设置为1代表TP,否则设置为0代表FP)。
FN (False Negative):对于一张图片中某一类别的所有gt边界框,除TP之外的记为FN。
Precision (准确率 / 精确率):「Precision is the ability of a model to identify only the relevant objects」,准确率是模型只找到相关目标的能力,等于TP/(TP+FP)。即模型给出的所有预测结果中命中真实目标的比例。
Recall (召回率):「Recall is the ability of a model to find all the relevant cases (all ground truth bounding boxes)」,召回率是模型找到所有相关目标的能力,等于TP/(TP+FN)。即模型给出的预测结果最多能覆盖多少真实目标。
一般来说,对于多分类目标检测的任务,会分别计算每个类别的TP、FP、FN数量,进一步计算每个类别的Precision、Recall。
AP (average Precision):平均精度,在不同recall下的最高precision的均值(一般会对各类别分别计算各自的AP)。
mAP (mean AP):平均精度的均值,各类别的AP的均值。
坡度
空间中的每一个点都可以确定无数个方向,而多元函数在某一点上必须有无数个方向。那么,无穷多的方向导数(直接反映函数此时的变化率的数量级)中最大的等于多少呢?它朝什么方向延伸?描述这个最大方向导数的向量和它所沿的方向就是我们所说的梯度。
梯度的本义是一个向量(vector),意思是一个函数在这个点的方向导数沿着这个方向取最大值,即函数沿着这个方向变化最快(这个梯度的方向) ) 此时,变化率最大(梯度的模数)。
文章出处登录后可见!
