条件概率

在进入朴素贝叶斯分类算法的学习之前，我们需要了解一些概率论的知识，我们先来看看条件概率。
条件概率是指某一事件A发生的可能性，表示P(A)。而条件概率指的是某一事件A已经发生了条件下，另一事件B发生的可能性，表示为P(B|A)。
怎么计算条件概率呢？设A,B是两个独立事件，且P(A)>0，称P(B|A)=P(AB)/P(A)为在事件A发生的条件下，事件B发生的条件概率。P(AB)表示事件A和B同时发生的概率。
例如：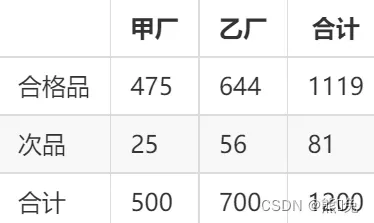
现在我想在知道产品是A厂生产的情况下，计算这个产品是次品的概率。这个时候，其实就是在计算条件概率。
假设事件A为产品是甲厂生产的，事件B为产品是次品，则根据表中数据可知P(AB)=25/1200 P(A)=500/1200 则P(B|A)=P(AB)/P(A)=25/500

贝叶斯公式

我们先来了解一下全概率公式的知识。简单来说，就是用全概率公式来达到某种目的，但达到目的的方法有很多种。如果你想知道通过所有方法可以达到目的的概率，使用全概率公式。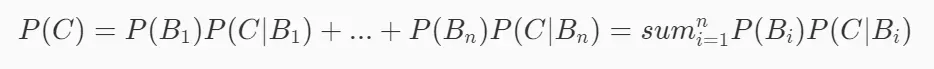

当导致一个事件发生的各种原因的概率已知时，我们要计算事件发生的概率，就可以使用全概率公式。但如果反过来，一个事件是已知发生的，但要计算该事件的各种原因的概率，我们需要使用贝叶斯公式。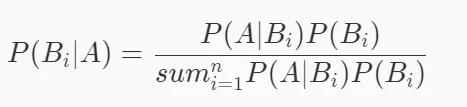

转换为简单的数学变换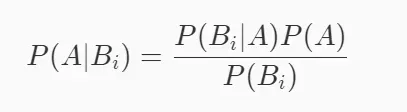

拉普拉斯平滑

零概率：在计算事件的概率时，如果某个事件在观察样本库（训练集）中没有出现过，会导致该事件的概率结果是0。但是对于实际情况来说这是不合理的，不能因为一个事件没有观察到，就被认为该事件一定不可能发生（即该事件的概率为0）。这时就需要我们的拉普拉斯平滑(Laplacian smoothing) 。
拉普拉斯平滑指的是，假设N表示训练数据集总共有多少种类别，Ni表示训练数据集中第i总共有多少种取值。则训练过程种在算类别的概率时分子加1，分母加N，算条件概率时分子加1，分母加Ni。

文本矢量化

由于数据集中每一条数据都是很长的一个字符串，所以我们需要对数据进行向量化的处理。例如，I have a apple！ I have a pen!可能需要将该字符串转换成向量如[10, 7, 0, 1, 2, 6, 22, 100, 8, 0, 1, 0]。sklearn提供了实现词频向量化功能的CountVectorizer类。想要对数据进行向量化

from sklearn.feature_ext\fraction.text import CountVectorizer
#实例化向量化对象  
vec = CountVectorizer()  
#将训练集中的新闻向量化  
X_train = vec.fit_transform(X_train)  
#将测试集中的新闻向量化  
X_test = vec.transform(X_test) 

但是仅仅通过统计词频的方式来将文本转换成向量会出现一个问题：长的文章词语出现的次数会比短的文章要多，而实际上两篇文章可能谈论的都是同一个主题。为了解决这个问题，我们可以使用tf-idf来构建文本向量，sklearn中已经提供了tf-idf的接口

from sklearn.feature_ext\fraction.text import TfidfTransformer
#实例化tf-idf对象  
tfidf = TfidfTransformer()  
#将训练集中的词频向量用tf-idf进行转换  
X_train = tfidf.fit_transform(X_train_count_vectorizer)  
#将测试集中的词频向量用tf-idf进行转换  
X_test = vec.transform(X_test_count_vectorizer) 

MultinomialNB

MultinomialNB是sklearn中多项分布数据的朴素贝叶斯算法的实现，并且是用于文本分类的经典朴素贝叶斯算法。在本关中建议使用MultinomialNB来实现文本分类功能。在MultinomialNB实例化时alpha是一个常用的参数。
alpha: 平滑因子。当等于1时，做的是拉普拉斯平滑；当小于1时做的是Lidstone平滑；当等于0时，不做任何平滑处理。

from sklearn.naive_bayes import MultinomialNB

clf = MultinomialNB()  
clf.fit(X_train, Y_train)  
result = clf.predict(X_test) 

来源：头曲