1. 人工蜂群算法介绍
人工蜂群算法自提出以来,以其参数少、自适应性强等特点受到众多研究者的追捧,并广泛应用于包括移动机器人路径规划领域在内的各个领域。
人工蜂群算法的数学模型
初始化会形成一个初始食物源。即初始解 (x1, x2, …, xn, …, xN) :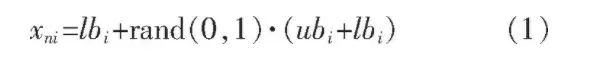
式中:lbi为可行解的最小值;ubi是可行解的最大值;rand (0, 1) 生成 (0, 1) 之间的随机数;n∈{1, 2, 3, …Fn}, Fn为食物源数目。
食物源生成之后, 评价函数会对生成的食物源进行评价, 评价函数如式 (2) 所示: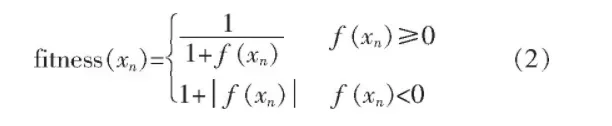
式中:f (xn) 为对应的解向量xn的目标函数值。
雇佣蜂在当前食物源附近搜索新食物源的方法如式 (3) 所示: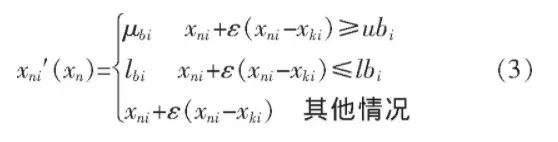
式中:xni′为新食物源;xni为当前食物源;ε为搜索系数, 其值介于[-1, 1]之间;xki是食物源中一个不同于xni的食物源, k∈{1, 2, 3, …Fn}。
当找到新的食物来源时,雇佣的蜜蜂会对新的食物来源进行评估,并与之前的食物来源进行比较,以决定放弃哪个食物来源。
观察蜂参照雇佣蜂返回时所带来的食物源信息进行选择觅食。它们会利用食物源的评价函数来计算他们选择某个食物源的可开采的概率probabilityn, 计算方法如式 (4) 所示: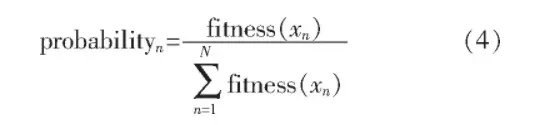
由于个体差异,观察蜜蜂会对食物来源有自己的期望。然后比较预期和可利用的概率,以确定蜜蜂是否选择这种食物来源进行采矿。
侦察蜂的作用是搜索新的食物源, 并不参照当前食物源, 而是类似初始化一样随机生成。在此之前会对选择次数超过限定值的食物源进行放弃, 如式 (5) 所示: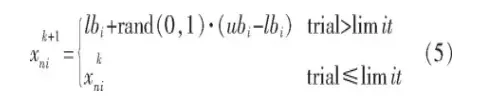
式中:trial是当前蜜蜂对食物源优化的次数。
2.部分源码
clc;
clear;
close all;
%% ABC + PSO Path Planning Problem
% 这里,系统试图找到起点之间的最优路径
%借助人工蜂群 (ABC) 算法的百分比和目的地点
% 和粒子群优化算法相结合。 这是个好策略
% 在机器人寻路中。 在每次运行中新位置的新障碍
% 定义和一条曲线试图找到最佳路径。 运行多次
% 以找到最佳结果。
%% 清除
clc;
clear;
warning('off');
%% 启动 ABC + PSO 最优路径查找器
model=Basics();
model.n=6; % 处理点数
CostFunction=@(x) Cost(x,model); % 成本函数
nVar=model.n; % 决策变量的数量
VarSize=[1 nVar]; % 决策变量矩阵的大小
VarMin.x=model.xmin; % 变量的下界
VarMax.x=model.xmax; % 变量的上限
VarMin.y=model.ymin; % 变量的下界
VarMax.y=model.ymax; % 变量的上限
%% PSO + ABC 参数
MaxIt=150; % 最大迭代次数
nPop=20; % 种群规模(群体规模)
w=1; % 惯性重量
wdamp=0.98; % 惯性重量阻尼比
c1=1.5; % 个人学习系数
c2=1.5; % 全局学习系数
nOnlooker = nPop; % 围观蜜蜂的数量
L = round(0.6*nVar*nPop); % 放弃限制参数(试用限制)
a = 1;
alpha=0.1;
VelMax.x=alpha*(VarMax.x-VarMin.x); % 最大速度
VelMin.x=-VelMax.x; %最小速度
VelMax.y=alpha*(VarMax.y-VarMin.y); % 最大速度
VelMin.y=-VelMax.y; % 最小速度
%% Initialization PSO + ABC
% 创建空粒子结构
empty_particle.Position=[];
empty_particle.Velocity=[];
empty_particle.Cost=[];
empty_particle.Sol=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
empty_particle.Best.Sol=[];
% 空蜂结构
empty_bee.Position = [];
empty_bee.Cost = [];
% 初始化全局最佳
GlobalBest.Cost=inf;
%初始化人口数组
pop = repmat(empty_bee, nPop, 1);
bee = repmat(empty_bee, nPop, 1);
% 初始化有史以来最好的解决方案
BestSol.Cost = inf;
GlobalBest.Cost=inf;
% 创建粒子矩阵
particle=repmat(empty_particle,nPop,1);
% 初始化循环
for i=1:nPop
% 初始化位置
if i > 1
particle(i).Position=CRSolution(model);
else
% 从源头到目的地的直线
xx = linspace(model.xs, model.xt, model.n+2);
yy = linspace(model.ys, model.yt, model.n+2);
particle(i).Position.x = xx(2:end-1);
particle(i).Position.y = yy(2:end-1);
end
%初始化速度
particle(i).Velocity.x=zeros(VarSize);
particle(i).Velocity.y=zeros(VarSize);
%评估
[particle(i).Cost, particle(i).Sol]=CostFunction(particle(i).Position);
% 更新个人最佳
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Sol=particle(i).Sol;
%更新全球最佳
if particle(i).Best.Cost<GlobalBest.Cost
GlobalBest=particle(i).Best;
end
end
% 初始化循环
for i=1:nPop
% 初始化位置
if i > 1
pop(i).Position=CRSolution(model);
else
% 从源头到目的地的直线
xx = linspace(model.xs, model.xt, model.n+2);
yy = linspace(model.ys, model.yt, model.n+2);
pop(i).Position.x = xx(2:end-1);
pop(i).Position.y = yy(2:end-1);
end
三、运行结果
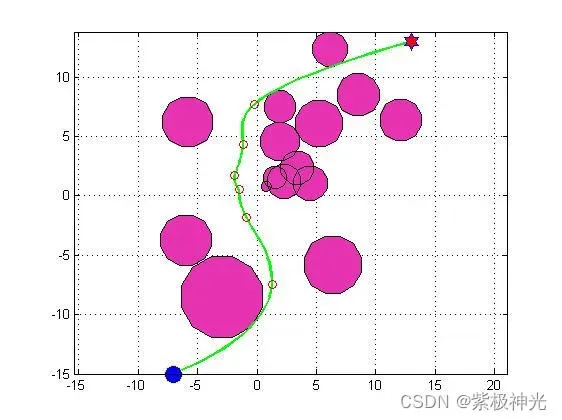
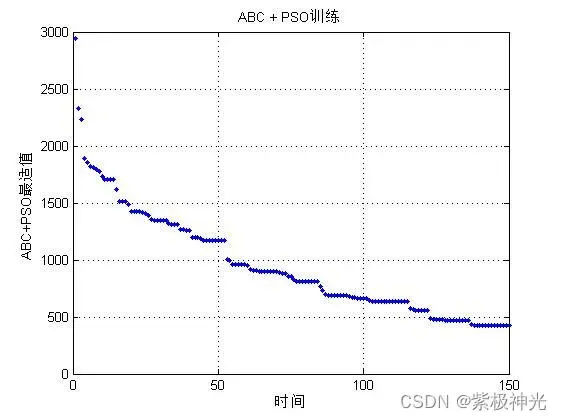
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]巫茜,罗金彪,顾晓群,曾青.基于改进PSO的无人机三维航迹规划优化算法[J].兵器装备工程学报。2021,42(08)
[4]方群,徐青.基于改进粒子群算法的无人机三维航迹规划[J].西北工业大学学报。2017,35(01)
[5]周国春,肖本贤.基于人工蜂群算法的机器人路径规划研究[J].自动化与仪表。2018,33(05)
文章出处登录后可见!
