一、Harris角点算法

Harris算法原理
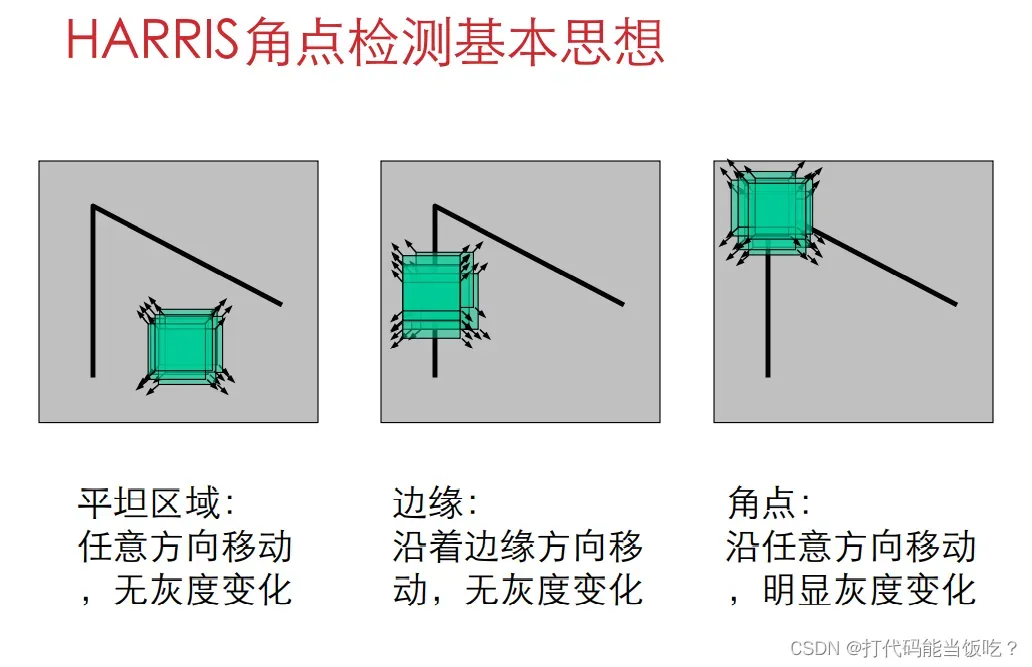
基本思想：如果一个像素周围有多个方向边缘，则认为该点为兴趣点，也称为角点。
Harris角点检测器可以给出图像中检测到兴趣点，但它并没有提供在图像间对兴趣点进行比较的方法，我们需要在每个角点添加描述子，以及对这些描述子进行比较，在图像中搜索有价值的特征点时，使用角点是一种不错的方法。 角点是很容易在图像中定位的局部特征， 并且大量存在于人造物体中（例如墙壁、 门、 窗户、 桌子等产生的角点）。 角点的价值在于它是两条边缘线的接合点， 是一种二维特征，可以被精确地定位（即使是子像素级精度）。 与此相反的是位于均匀区域或物体轮廓上的点以及在同一物体的不同图像上很难重复精确定位的点。 Harris特征检测是检测角点的经典方法。
拐角检测

该算法的基本思想是利用一个固定的窗口将图像向任意方向滑动。比较滑动前后的两种情况，以及窗口中像素的灰度变化程度。如果有任何方向的滑动，都会有很大的灰度。度变化，那么我们可以认为窗口中有角落。

二、Harris代码实现

拐角检测

# 局部图像描述子
# Harris角点检测
from pylab import *
from PIL import Image
from numpy import *
from scipy.ndimage import filters

def compute_harris_response(im, sigma=3):
    """在一幅灰度图像中，对每个像素计算Harris角点检测器响应函数"""
    # 计算导数
    imx = zeros(im.shape)
    filters.gaussian_filter(im, (sigma, sigma), (0, 1), imx)
    imy = zeros(im.shape)
    filters.gaussian_filter(im, (sigma, sigma), (1, 0), imy)
    # 计算Harris矩阵的分量
    Wxx = filters.gaussian_filter(imx * imx, sigma)
    Wxy = filters.gaussian_filter(imx * imy, sigma)
    Wyy = filters.gaussian_filter(imy * imy, sigma)
    # 计算特征值和迹
    Wdet = Wxx * Wyy - Wxy ** 2
    Wtr = Wxx + Wyy
    return Wdet / Wtr


def get_harris_points(harrisim, min_dist=10, threshold=0.1):
    """从一幅Harris响应图像中返回角点。min_dist为分割角点和图像边界的最小像素数目"""
    # 寻找高于阈值的候选角点
    corner_threshold = harrisim.max() * threshold
    harrisim_t = (harrisim > corner_threshold) * 1
    # 得到候选点的坐标
    coords = array(harrisim_t.nonzero()).T
    # 以及它们的Harris响应值
    candidate_values = [harrisim[c[0], c[1]] for c in coords]
    # 对候选点按照Harris响应值进行排序
    index = argsort(candidate_values)
    # 将可行点的位置保存到数组中
    allowed_locations = zeros(harrisim.shape)
    allowed_locations[min_dist:-min_dist, min_dist:-min_dist] = 1
    # 按照min_distance原则，选择最佳Harris点
    filtered_coords = []
    for i in index:
        if allowed_locations[coords[i, 0], coords[i, 1]] == 1:
            filtered_coords.append(coords[i])
            allowed_locations[(coords[i, 0] - min_dist):(coords[i, 0] + min_dist),
            (coords[i, 1] - min_dist):(coords[i, 1] + min_dist)] = 0
    return filtered_coords

def plot_harris_points(image,filtered_coords):
    """绘制图像中检测到的角点"""
    figure()
    gray()
    imshow(image)
    plot([p[1] for p in filtered_coords],[p[0] for p in filtered_coords],'*')
    axis('off')
    show()
# 调用展示
im = array(Image.open('中山.jpg').convert('L'))
harrisim = compute_harris_response(im)
filtered_coords = get_harris_points(harrisim,6, 0.2)
plot_harris_points(im, filtered_coords)

运行截图：

特征匹配

from PIL import Image
from numpy import *
import harris
from pylab import *
wid=5
im1=array(Image.open('中山.jpg').convert('L'))
im2=array(Image.open('中山1.jpg').convert('L'))
harrisim=harris.compute_harris_response(im1,5)
filtered_coords1=harris.get_harris_points(harrisim,wid+1,0.2)
d1=harris.get_descriptors(im1,filtered_coords1,wid)
harrisim=harris.compute_harris_response(im2,5)
filtered_coords2=harris.get_harris_points(harrisim,wid+1,0.2)
d2=harris.get_descriptors(im2,filtered_coords2,wid)
print ('starting matching')
matches=harris.match_twosided(d1,d2)
figure()
gray()
harris.plot_matches(im1,im2,filtered_coords1,filtered_coords2,matches)
show()

运行截图

三、SIFT特征匹配算法

注：需要提前进行VLfeat配置
下载网址：http://www.vlfeat.org/
选择vlfeat-0.9.20-bin.tar.gz版本，解压后把bin文件夹里的win32文件夹里的sift.exe、vl.dll、vl.lib 拷到你所在的项目文件夹下
SIFT简介
SIFT，即尺度不变特征变换（Scale-invariant feature transform，SIFT），是用于图像处理领域的一种描述。这种描述具有尺度不变性，它对物体的尺度变化，刚体变换，光照强度和遮挡都具有较好的稳定性，可在图像中检测出关键点，是一种局部特征描述子。

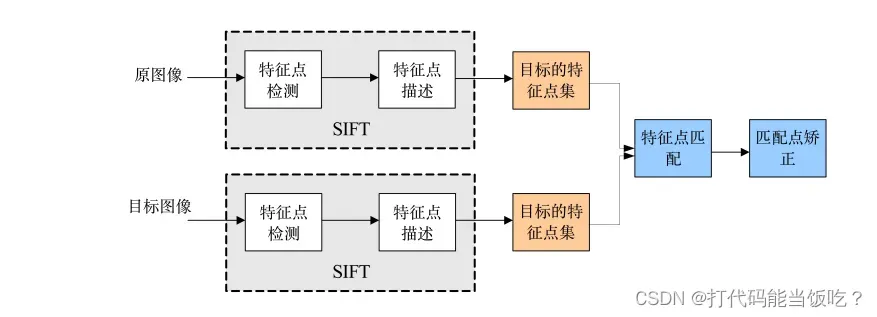
SIFT 算法被认为是图像匹配效果好的方法之 一算法实现特征匹配主要有三个流程：
① 特征点提取；
②确定特征点的主方向；
③ 特征点描述；
④ 特征点匹配；

其中特征点提取主要包括生成高斯差分（DifferenceofGaussian，DOG）尺度空间、寻找局部极值点、特征点筛选、确定特征点方向；特征点匹配主要包括根据描述子相似性进行匹配、匹配对比值提纯、RANSAC方法剔除离群匹配对。
SIFT算法的特点:

稳定性 唯一性 丰富性 高速 可扩展性

SIFT算法可以的解决问题：

目标的旋转、缩放、平移（RST）
图像放射/投影变换（视点viewpoint）
光照影响（illumination）
部分目标遮挡（occlusion）
杂物场景（clutter）
噪音

4.SIFT特征点匹配

运行代码：

from PIL import Image
from pylab import *
import sys
from PCV.localdescriptors import sift
 
if len(sys.argv) >= 3:
    im1f, im2f = sys.argv[1], sys.argv[2]
else:
    im1f = '中山.jpg'
    im2f = '中山1.jpg'
im1 = array(Image.open(im1f))
im2 = array(Image.open(im2f))
 
sift.process_image(im1f, 'out_sift_1.txt')
l1, d1 = sift.read_features_from_file('out_sift_1.txt')
figure()
gray()
subplot(121)
sift.plot_features(im1, l1, circle=False)
 
sift.process_image(im2f, 'out_sift_2.txt')
l2, d2 = sift.read_features_from_file('out_sift_2.txt')
subplot(122)
sift.plot_features(im2, l2, circle=False)
 
# matches = sift.match(d1, d2)
matches = sift.match_twosided(d1, d2)
print('{} matches'.format(len(matches.nonzero()[0])))
 
figure()
gray()
sift.plot_matches(im1, im2, l1, l2, matches, show_below=True)
show()

运行结果：

五、Harris与SIFT算法比较

harris角点检测是一种直接基于灰度图像的角点提取算法，稳定性高，尤其对L型角点检测精度高，但由于采用了高斯滤波，运算速度相对较慢，角点信息有丢失和位置偏移的现象，而且角点提取有聚簇现象。
从理论上说，SIFT是一种相似不变量，即对图像尺度变化和旋转是不变量。然而，由于构造SIFT特征时，在很多细节上进行了特殊处理，使得SIFT对图像的复杂变形和光照变化具有了较强的适应性，同时运算速度比较快，定位精度比较高。如：
在多尺度空间采用DOG算子检测关键点，相比传统的基于LOG算子的检测方法，运算速度大大加快；关键点的精确定位不仅提高了精度，而且大大提高了关键点的稳定性；
在构造描述符时，以子区域的统计属性为研究对象，而不是单个像素，提高了对图像局部变形的适应性。
计算速度： SIFT>HARRIS
旋转鲁棒性： SIFT>HARRIS