1) 阅读题目,了解题目大意
(1)首先,题目中需要我们实现一个SNN的模拟器,有三个部分:1、神经元,神经元有内部自己的状态,且按照一定公式在更新,而且可以接受和发放脉冲。2、脉冲源,在特定的时间发放脉冲。3、突触,连接神经元与神经元或脉冲源与神经元,负责传递脉冲。
- 从以上信息我们可以了解到,大致的画面如下:
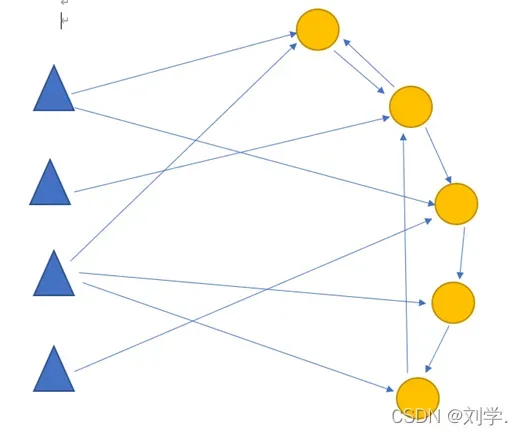
- 蓝色三角形代表脉冲源,黄色圆圈代表神经元,蓝色箭头代表突触,箭头方向代表脉冲传播方向。请注意,脉冲源不接受脉冲信号,但神经元可以接收和发送信号。因此,如标题“Synapses表示神经元-神经元和脉冲源-神经元之间的连接,包括一个传入节点和一个传出节点(可能存在自环和多重边)”正好匹配,说明上述模型符合题主的要求。
(2)其次,先来了解神经元的特点,题目中,“神经元会按照一定的规则更新自己的内部状态。”中的规则指的就是公式: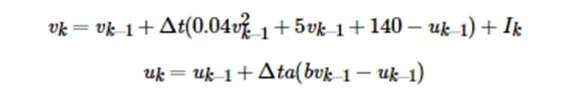
- 而状态则指的是描述神经元的两个变量v和u,公式表明,v和u受到常量a和b和Ik的影响,而a和b是常量,而Ik表示,k时刻神经元受到的所有脉冲信号的强度之和,而该公式也是用k-1时刻的取值来计算k时刻这两个变量的取值。当进行该公式的计算后,如果满足k时刻v的值大于等于30,则神经元会发射一个脉冲(注意,此时未说明脉冲的大小),且会重置神经元的内部状态,即内部参数v和u的值,重置规则为k时刻,v
= c,u = u+d。
(3)然后,来了解突触的特点,突触自身有一个入结点和出结点,且从入结点传入脉冲后,会有一个传播延迟D,即D时刻后脉冲信号才能到达出结点。注意:题目中已经指出,出结点此时会受到一个强度为w的脉冲。这个条件很重要,这说明,当突触的上个神经元满足题目所给的条件后,会发射一个脉冲,但脉冲信号的大小并不取决去上一个神经元,而取决去传播它的突触。
(4)最后,脉冲源的特性,脉冲源不接受脉冲信号,只在随机的时间发送信号,而为了实现这个随机过程,题目规定,每个脉冲源有一个参数r,在每个时刻,按照编号顺序从小到大,每个脉冲源调用一次上述的伪随机函数,当r大于这个伪随机函数的值时,在当前时间刻发放一次脉冲,并通过突触传播到神经元。伪随机函数题目已经给出:
static unsigned long next = 1;
/* RAND_MAX assumed to be 32767 */
int myrand(void) {
next = next * 1103515245 + 12345;
return((unsigned)(next/65536) % 32768);
}
- 这个伪随机函数产生的随机数实际上是固定的。例如,前十个随机数是:
16838
5758
10113
17515
31051
5627
23010
7419
16212
4086
- 值得注意的是,所有的脉冲源是按顺序依次调用的伪随机函数,也就是说伪随机函数的值在是依次被脉冲源依次使用的。比如有两个脉冲源,则在1时刻16838这个随机数用于第一个脉冲源,而后5758这个随机数用于第二个脉冲源,而只有两个脉冲源,所以下一个随机数10113则是在2时刻,用于第二个脉冲源,而后以此类推,每个随机数不会被用重复使用,这个特点很重要,下面会讲到。
2) 模拟题目的推导过程
(1)在模拟之前,我们需要了解题目所要求的编号问题,规定输入数据中结点按如下方式顺序编号:[0,N−1]为神经元的编号,[N,N+P−1]为脉冲源的编号,也就是说,编号时,先从神经元从0开始编号,所有神经元编号结束后,脉冲源从下一个编号值继续编号。这里以样例1的编号为例,不需要过多赘述。
(2)了解题目的输入,除了上文提到的各个组成部分的状态参数外,还需要知道时间T,题目中的“进行仿真的时候,已知0时间刻各个神经元的状态,从1时间刻开始按照上述规则进行计算,直到完成T时刻的计算”表示整个的仿真时间。但在仿真时,我们只需要每隔Dt个时间记录一次各神经元的状态,而刚好,各神经元的状态变化也与Dt有关,即题目规定,神经元的状态变的时刻刚好都是Dt的整数倍。
(3)首先,模拟样例1的推导过程,样例1的输入为:
1 1 1 10
0.1
1 -70.0 -14.0 0.02 0.2 -65.0 2.0
30000
1 0 30.0 2
- 从题目要求的输入可以看出,该样例有1个神经元、1个突触和1个脉冲源,整个模拟时间为10,时间间隔Δt==0.1。唯一的脉冲源通过脉冲强度为30.0,传播延迟为2的突触传播到唯一的神经元。脉冲源是否发送脉冲所需的判断参数r为30000。则易知,共有10个记录时刻,根据从上文伪随机函数的调用特点,我们知道,需要前10个伪随机数,而根据伪随机函数生成的前10个数在上文已经给出,再由参数r判断出,该唯一的脉冲源在时刻1-4和6-10发放脉冲。

- 在这里,我们可以列出一个表格来方便地表示每个时刻神经元的状态:
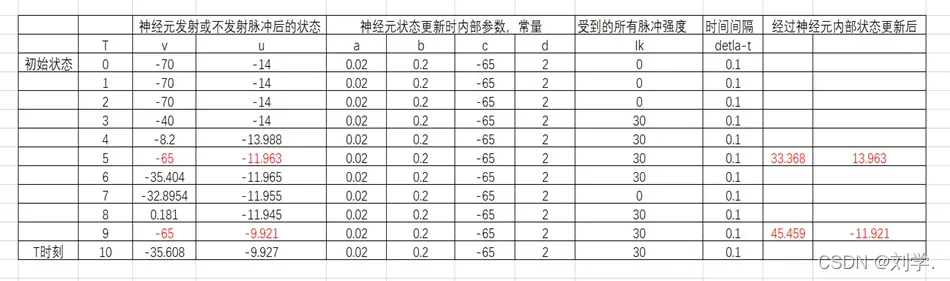
- 注意,唯一的脉冲源在时刻1-4和6-10发放脉冲,但由于突触有2个时刻的延迟,所以在表中的Ik表示的k时刻该唯一的神经元受到的这唯一的脉冲信号的强度,在3-6时刻才能受到,初始时刻为0时刻,该神经元的各个参数v,u,a,b,c,d由标准输入给出,再由神经元内部状态更新公式,得到1时刻的神经元各个状态参数的值,然后以此类推,就能得到所有时刻的神经元的状态参数的值,注意,当计算到4时刻后,再经过神经元内部状态更新公式计算发现5时刻时的v值等于33.368大于了30,该此时神经元会发射一个脉冲,且会重置神经元的内部状态,即内部参数v和u的值,重置规则上文和题目已经说到,重置后,5时刻v的值为-65,u的值为-11.963,已用红色字体标出,以下同理。
(4)为了把整个过程的推导了解的更清晰,我们来模拟样例2的推到过程,仅仅只由一个神经元和脉冲源并不能说明其特点,样例2的输入为:
2 4 2 10
0.1
1 -70.0 -14.0 0.02 0.2 -65.0 2.0
1 -69.0 -13.0 0.04 0.1 -60.0 1.0
30000
20000
2 0 15.0 1
3 1 20.0 1
1 0 10.0 2
0 1 40.0 3
- 该样例中有2个神经元、4个突触和2个脉冲源,时间间隔Δt=0.1,根据上文提到的编号规则和题目中要求的s,t分别表示入结点和出结点的编号可知脉冲源与神经元和突触的连接关系,画出示意图:

- 注意,此时是两个脉冲源,根据上文伪随机函数调用规则,和输入的Δt=0.1,仿真时间T等于10可知仿真期间共有10个记录时刻,每个记录时刻两个脉冲源都需要用到不同的伪随机函数,所以需要前20个伪随机函数。
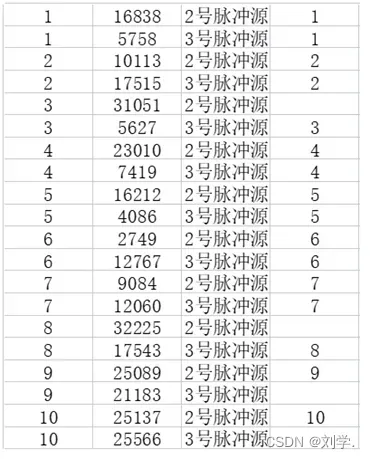
- 再根据两个脉冲源的r值判断两个脉冲源发射脉冲的时刻,可知2号脉冲源在时刻1,2,4,5,6,7,9,10发射脉冲,3号脉冲源在时刻1,2,3,4,5,6,7,8发射脉冲。
这里我们还是用一张表来记录两个神经元在每一时刻的状态: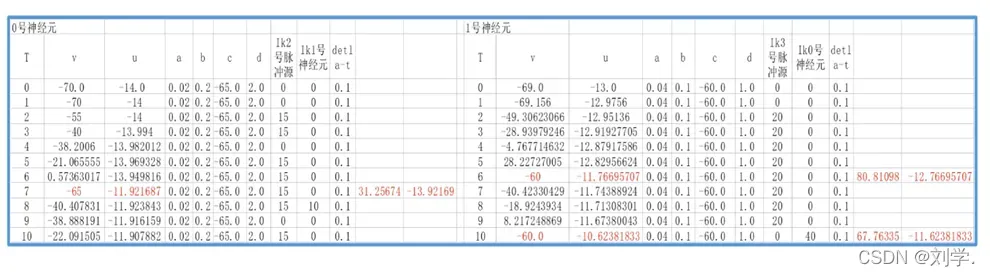
分析方式同样例1。
3) 阅读输入输出格式,了解题目的要求
(1)根据题目要求,“输出共有两行,第一行由两个近似保留 3 位小数的实数组成,分别是所有神经元在时刻 T 时变量 v 的取值的最小值和最大值。第二行由两个整数组成,分别是所有神经元在整个模拟过程中发放脉冲次数的最小值和最大值”我们知道,我们需要记录各个神经元的脉冲次数并比较大小找出最值,和最后T时刻即最后记录时刻各个神经元的v值并比较大小并找出最值。
4) 确认以上推导过程和原问题一致
(1)根据样例1和2的模拟推导过程,按题目要求找出答案,根据对样例1模拟的表格可知,T时刻只有唯一一个神经元的v值,即-35.608既是最大值也是最小值,唯一神经元发放脉冲次数为2,既是最大值也是最小值。
根据对样例2的模拟的表格可知,T时刻0号神经元的v值-22.092为最大值,1号神经元的v值-60.000为最小值,0号神经元发送脉冲次数1为最小值,1号神经元发送脉冲次数2为最大值。
(2)与题目所给的样例输出一致,说明以上推导过程合理。
5) 分析且完成推导过程所需的结构体
(1)首先神经元的各个参数v,u,a,b,c,d是表示神经元内部的状态,可以定义一个结构体数组NN[1000]表示神经元,其内部元素包含这几个参数,又由我们上述推导过程知道,要记录参数v,u还需要v和u的前一时刻的值v_pre和u_pre,所以我们也可以加入结构体中:
struct neural{
double v_pre, u_pre;
double v, u;
double a, b, c, d;
}NN[1000];
(2)突触的结构体,首先肯定包含入结点编号,出结点编号,又因为上文已经解释过,脉冲强度其实由突触决定的,所以记录在突触结构体中。如果再对比突触编号规则与脉冲源和神经元编号规则可知,其实用的是同一套编号,即只要知道突触的入结点编号和出结点编号,就能知道突触的连接方向和位置,在样例2的模拟中应该已经有体验,所以也只记录到突触结构体中:
struct edg{
int from, to; //突触的入结点编号,出结点编号
double w; //在该突触上传播的脉冲强度,虽然脉冲是神经元或脉冲源发射脉冲
//但由于突触的方向是单向的,所以,可以只记录传播时的脉冲强度
int D; //突触上的传播延迟
}e[1000];
(3)此外还有:
int r[1000]; //用来存储每个脉冲源的参数,即r
double IK[1000][10000] = {0};
//记录突触的某个时刻出结点和延迟后时间的突触传播的强度 ,即某个强度,什么时刻,到达某个出结点
//又因为出结点的编号恰好与神经元对应,即到达的是某个编号的神经元
6) 直接得到程序
#include <iostream>
#include <cstring>
using namespace std;
static unsigned long Next = 1;
//RAND_MAX assumed to be 32767
int myrand(void) //题目中已给出的伪随机数生成函数
{
Next = Next * 1103515245 + 12345;
return((unsigned)(Next/65536)%32768);
}
int N, S, P, T;
double Dt; //Delta_t 时间间隔
//定义存储结构体,神经元和突触
int rn;
struct neural{
double v_pre, u_pre; //神经元内状态参数v和u的前一时间间隔整数倍的时刻,即前一记录时刻的状态
double v, u; //神经元内状态v和u为当前记录时刻的状态
double a, b, c, d; //神经元内的其他参数,常量 ,a和b是用来通过上一记录时刻计算此时记录时刻的状态所需要用到的参数
//c和d是当该神经元某时刻受到所有脉冲之和大于或等于30时,用来再次重置v和u
}NN[1000];
int r[1000]; //用来存储每个脉冲源的参数,即r
double IK[1000][10000] = {0}; //记录突触的某个时刻出结点和延迟后时间 的突触传播的强度 ,即某个强度,什么时刻,到达某个出结点
//又因为出结点的编号恰好与神经元对应,即到达的是某个编号的神经元
struct edg{
int from, to; //突触的入结点编号,出结点编号
double w; //在该突触上传播的脉冲强度,虽然脉冲是神经元或脉冲源发射脉冲
//但由于突触的方向是单向的,所以,可以只记录传播时的脉冲强度
int D; //突触上的传播延迟
}e[1000];
//按题目要求输入
int main()
{
scanf("%d %d %d %d", &N, &S, &P, &T); //N个神经元,S个突触,P个脉冲源,从0时刻仿真到T时刻
scanf("%lf", &Dt); //仿真期间,每隔Dt的时间间隔记录一次
int rn; //具有相同初始状态v,u和内部参数a,b,c,d的神经元个数
double vv, uu, aa, bb, cc, dd; //初始时即0时刻时,神经元的状态,和自己设置的四个参数
int sum = 0;
while(sum<N) //输入神经元的参数
{
scanf("%d %lf %lf %lf %lf %lf %lf", &rn, &vv, &uu, &aa, &bb, &cc, &dd);
for(int i=sum; i<sum+rn; i++)
{
NN[i].v_pre = NN[i].v = vv;
NN[i].u_pre = NN[i].u = uu;
NN[i].a = aa;
NN[i].b = bb;
NN[i].c = cc;
NN[i].d = dd;
}
sum = sum + rn;
}
for(int i=0; i<P; i++)
scanf("%d", &r[i]); //输入每个脉冲源的参数,用来和伪随机数作比较,以判断是否发出脉冲信号
//存放在r数组中
for(int i=0; i<S; i++) //输入每个突触的参数
{
int ff, tt;
double ww;
int DD;
scanf("%d %d %lf %d", &ff, &tt, &ww, &DD);
e[i].from = ff; //突触的入结点编号
e[i].to = tt; //突触的出结点编号
e[i].w = ww; //突触传播的脉冲强度 ,突触出结点所受到的脉冲
e[i].D = DD; //突触的传播延迟
}
//计算所有脉冲源在1到T时刻,是否会发送脉冲,
//并将脉冲强度值赋值到连接的神经元IK中
for(int t=1; t<T; t++) //遍历每个记录时刻
{
for(int i=0; i<P; i++) //遍历每个脉冲源,
{
if(r[i]>myrand()) //依次判断每个脉冲源是否发送脉冲信号
{
for(int j=0; j<S; j++) //若脉冲源要发射脉冲,遍历每个突触
{
if((e[j].from == i+N) && (t+e[j].D <= T)) //因为脉冲源的编号排在神经元之后,而神经元的数量为N,而i在【0,p】之间,所以脉冲源的编号在【N,N+i】之间
{ //如果突触的入结点编号等于脉冲源编号, 且当前记录时刻加上在突触上的延时时间,还在仿真时间内
IK[e[j].to][t+e[j].D] = e[j].w; //则把当前突触传播的脉冲强度,用IK记录,突触的出结点,和延迟后的时刻 ,即突触的出结点所连接的神经元接受脉冲的时刻
}
}
}
}
}
//计算每个时刻,每个神经元按照公式计算。
//如果满足条件,发出脉冲。
int cnt[1000] = {0};
for(int t=1; t<=T; t++) //每个时刻判断一次所有的神经元
{
for(int i=0; i<N; i++) //遍历每个神经源
{
NN[i].v = NN[i].v_pre + Dt*(0.04*NN[i].v_pre*NN[i].v_pre + 5*NN[i].v_pre + 140.0 - NN[i].u_pre) + IK[i][t];
NN[i].u = NN[i].u_pre + Dt*NN[i].a*(NN[i].b*NN[i].v_pre - NN[i].u_pre);
if (NN[i].v >= 30) //如果神经元内v的值满足条件
{
cnt[i]++; //则发射脉冲 ,记录神经元发射的脉冲次数
NN[i].v = NN[i].c;
NN[i].u = NN[i].u + NN[i].d; //如题,重置神经元内部参数
for(int j=0; j<S; j++) //遍历每个突触
{
if((e[j].from == i) && (t+e[j].D <= T)) //突触的入结点等于若神经元的编号,且延迟后在时间范围内
{
IK[e[j].to][t+e[j].D] += e[j].w; //则把突触的出结点所连接的神经元在当前时刻延迟后所收的的脉冲,加上当前时刻的脉冲
}
}
}
NN[i].v_pre = NN[i].v;
NN[i].u_pre = NN[i].u; //更新神经元内部的参数,每过一个纪录时刻,神经元内参数的当前时刻状态就变成了前一时刻的状态
}
}
//遍历每个神经元,求得T时刻的最值和发送脉冲数的最值
double minv = NN[0].v, maxv = NN[0].v; //存储所有神经元的v的最值
int mincnt = cnt[0], maxcnt = cnt[0]; 存储所有神经元的脉冲次数的最值
for(int i=1; i<N; i++) //遍历每个神经元
{
if(minv > NN[i].v) minv = NN[i].v; //寻找所有神经元V的最小值,并记录
if(maxv < NN[i].v) maxv = NN[i].v; //寻找所有神经元V的最大值,并记录
if(mincnt > cnt[i]) mincnt = cnt[i];
if(maxcnt < cnt[i]) maxcnt = cnt[i]; //同理
}
printf("%.3lf %.3lf\n", minv, maxv); //输出结果
printf("%d %d\n",mincnt, maxcnt);
return 0;
}
7)运行结果
- 样例1数据测试
1 1 1 10
0.1
1 -70.0 -14.0 0.02 0.2 -65.0 2.0
30000
1 0 30.0 2
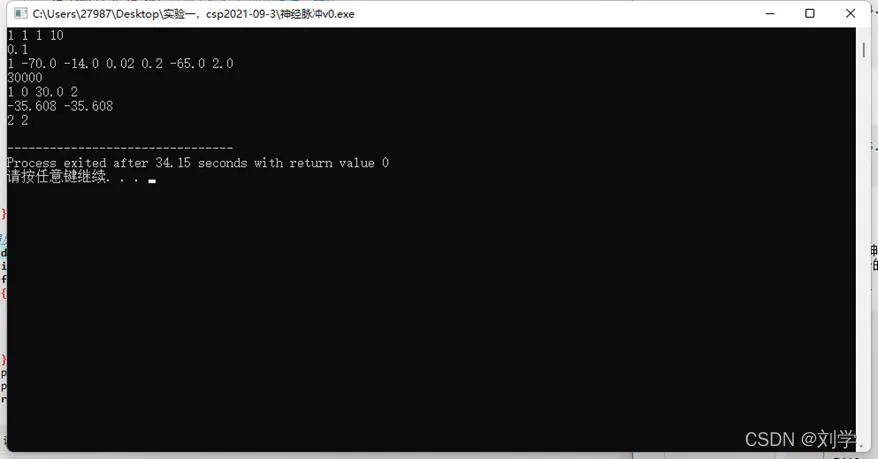
结果是正确的。
- 样例2数据测试
2 4 2 10
0.1
1 -70.0 -14.0 0.02 0.2 -65.0 2.0
1 -69.0 -13.0 0.04 0.1 -60.0 1.0
30000
20000
2 0 15.0 1
3 1 20.0 1
1 0 10.0 2
0 1 40.0 3
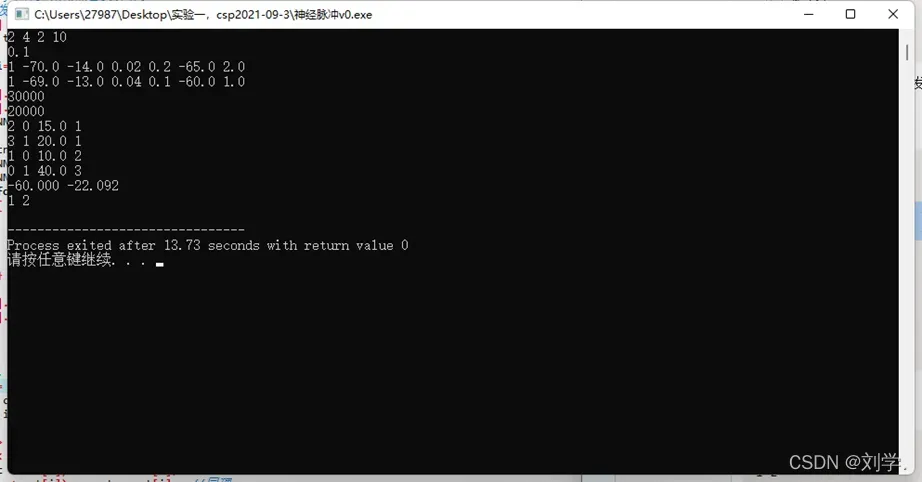
结果是正确的。
8)结果分析
- 项目评估
- 上述程序可以正确运行,得到了预期的结果。所有样本都正确,说明程序逻辑正确,提交测试后的分数不全,可能是时空运行成本的代价。
- 运营成本
- 运行时所需要的存储单元为1000个元素的两个结构体数组和一个一维数组和一个二维素组,以及4+1+6* N+P+4* S+2个普通变量。所以空间复杂度为O(n)。
- 在计算所有脉冲源在1到T时刻,是否会发送脉冲时,若脉冲源要发射脉冲,遍历每个突触,并将脉冲强度值赋值到连接的神经元IK中,循环的次数为最多为T* P* S,最少为T*P。
- 计算每个时刻,每个神经元按照公式计算,如果满足条件,发出脉冲。遍历每个记录时刻,遍历每个神经源,遍历每个突触,循环次数为T* N* S。所以时间复杂度为O(n^3)。
- 不满意的地方
- 时间复杂度太高,说明算法效率低,需要进一步改进。
文章出处登录后可见!
